Обчислюваність і вирішуваність

Таким чином, всякий алгоритм, описаний в термінах частково-рекурсивних функцій, можна реалізувати машиною Тьюрінга і навпаки. Звідси слідує, що будь-які твердження про існування або неіснування алгоритмів, зроблені в одній з цих теорій, вірні і в іншій. У поєднанні з тезою Черча-Тьюрінга це означає, що такі твердження можна формулювати для алгоритмів взагалі, не фіксуючи конкретну модель і використовуючи результати обох теорій. Таким чином, можливий виклад теорії алгоритмів, інваріантний по відношенню до способу формалізації поняття «алгоритм», при будь-якій формалізації основні властивості алгоритмів залишаються тими ж самими. Основні поняття такої інваріантної теорії (будемо називати її загальною теорією алгоритмів) - це алгоритм (рекурсивний опис функції, система команд машини Тьюрінга або опис в якій-небудь іншій моделі; вважається, що вибрана якась модель, але яка саме - не є важливим) і обчислювана функція. Функція називається обчислюваною, якщо існує обчислюючий її алгоритм. При цьому неістотно, числова функція це чи ні. Термін «загальнорекурсивна функція», вжитий в інваріантному значенні, є синонімом терміну «всюди визначена обчислювана функція».

Еквівалентність тверджень «функція f обчислювана» і «існує алгоритм,що обчислює функцію f» іноді приводить до змішення понять алгоритму і обчислюваної функції; зокрема, кажучи про рекурсивну функцію, часто мають на увазі її конкретний рекурсивний опис. Насправді ж відмінність між обчислюваною функцією і алгоритмом - це відмінність між функцією і способом її задання. Без дотримання цих відмінностей неможлива коректна інтерпретація деяких важливих результатів теорії алгоритмів. У той же час традиція викладу теорії алгоритмів дозволяє не розрізнювати поняття алгоритму і функції в тих випадках, коли це не приводить до плутанини.

У цьому параграфі резюмуються вже отримані і формулюються деякі нові поняття і результати теорії алгоритмів саме в їх інваріантному вигляді. Вони вірні для будь-якої формалізації поняття «алгоритм», що не заважає використати в кожному конкретному міркуванні конкретну алгоритмічну модель, найбільш відповідну для даного випадку.

Нумерація алгоритмів. Множина всіх алгоритмів - рахункова. Цей факт вже відмічався, однак він ясний і без звернення до конкретних алгоритмічних моделей: адже будь-який алгоритм можна задати кінцевим описом (наприклад, в алфавіті знаків, що використовуються при наборі математичних книг), а множина всіх кінцевих слів в фіксованому алфавіті - рахункова. Рахунковість множини алгоритмів означає наявність взаємно однозначної відповідності між алгоритмами і числами натурального ряду, тобто функції типу j: N®Al,що взаємно однозначно відображає в слова в алфавіті Аl, вибраному для опису алгоритмів, числа натурального ряду. Така функція j(n)=A називається нумерацією алгоритмів, а її аргумент n – номером алгоритму А при нумерації j. З взаємної однозначності відображення j слідує існування зворотної функції j^-1(A_n)=n, що поновлює за описом алгоритму An його номер n.

Фактично ми вже побудували одну нумерацію: алфавіт Аl і спосіб представлення алгоритмів в цьому алфавіті вибрані при побудові універсальної машини U, а функція j визначається методом числового кодування конфігурацій, використаним при доведенні теореми 5.7. Правда, при такому визначенні нумерація j деякі натуральні числа декодує в слова, що не є записом ніякого алгоритму. Ці числа можна вважати номерами ніде не визначених алгоритмів, а відповідну універсальну машину визначити так, щоб на цих словах вона зациклювалась.

Наведений приклад показує, що існують обчислювані нумерації. Очевидно, що різних нумерацій багато, ми не будемо займатися їх особливостями, а домовимося, що зафіксована якась обчислювана нумерація. Основний інтерес для додатків теорії алгоритмів представляють інваріантні властивості номерів алгоритмів, що не залежать від особливостей вибраної нумерації.

Нумерація всіх алгоритмів є одночасно і нумерацією всіх обчислюваних функцій в наступному значенні: номер функції f - це номер деякого алгоритму, що обчислює f. В будь-якій нумерації всяка функція буде мати нескінченну множину різних номерів. Це ясно з того, що до будь-якої машини Тьюрінга можна додати будь-яку кількість недосяжних станів (тобто станів, що не зустрічаються в правих частинах команд); всі отримані машини мають різні номери, але обчислюють одну і ту ж функцію. Кажучи про нумерацію, будемо вважати що вона вибрана так, що A₀ і функція f_o, що обчислюється ним, ніде не визначені.

Існування нумерацій дозволяє працювати з алгоритмами як з числами. Це особливо зручно при дослідженні алгоритмів над алгоритмами. Такі алгоритми вже розглядалися при побудові універсальної машини Тьюрінга і в зв'язку з проблемою зупинки. Отримані результати тепер можна сформулювати в інваріантному вигляді.

Теорема 5.9. Існує універсальний алгоритм U (х, у), такий, що для будь-якого алгоритму А з номером j^-1(A) U(j^-1(A),у) = А (у), в інших позначеннях U(х, у)=А_х (у).

Для конкретної нумерації j* ця теорема доведена в § 4.2 побудовою універсальної машини Тьюрінга. Для будь-якої іншої обчислюваної нумерації j можна вибрати один з двох шляхів:

a) побудувати новий універсальний алгоритм, працюючий безпосередньо з номерами, що породжуються j;

b) побудувати алгоритм перекладу (взаємно однозначного відображення) j в j *.

По суті, обчислювана нумерація служить мовою програмування для універсального алгоритму. Шлях «а» - це побудова нової машини для кожної нової мови, шлях «б» – побудова нового транслятора для колишньої машини.

Теорема 5.4`. Не існує алгоритму, який за номером х будь-якого алгоритму і початковими даними у визначав би, зупиниться алгоритм при цих даних чи ні; інакше кажучи, не існує алгоритму В (х, у) такого, що для будь-якого алгоритму А_х (з номером ¹(A)=x)

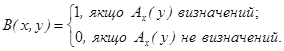
Ця теорема-переформулювання у інваріантному вигляді теореми 5.4 про нерозв'язність проблеми зупинки.

Один окремий випадок проблеми зупинки має цілком самостійну інтерпретацію. При доведенні теореми 5.4 була розглянута машина T_i, яка вирішувала проблему зупинки для машини Т у випадку, коли на стрічці машини Т написана її власна система команд. Така проблема називається проблемою самозастосованності машин Тьюрінга. Було показано, що така машина неможлива. У інваріантному вигляді відповідне твердження формулюється так.

Теорема 5.10. Проблема самозастосування алгоритмів алгоритмічно нерозв'язна: не існує алгоритму B₁(х), такого, що для будь-якого алгоритму Ах

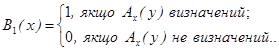(5.8)

Зазначимо, що самозастосування - окремий випадок проблеми зупинки, і саме тому теорему 5.10 не можна отримати з теореми 5.4' простою підстановкою х замість у в В (х, у): окремий випадок алгоритмічно нерозв'язної проблеми може виявитися і вирішуваним.

Теореми 5.4' і 5.10 є могутнім засобом для доведення усіляких нерозв'язностей.

Розв’язання задачі переліку всіх алгоритмів (і, зокрема, всіх рекурсивних функцій) досить ясне, принаймні в принципі. Могло б показатися, що перелік примітивно-рекурсивних або загальнорекурсивних функцій виявиться більш легкою справою. Однак, це не так.

Теорема 5.11. Для будь-якого переліку будь-якої множини S всюди визначенних обчислюваних (тобто загальнорекурсивних) функцій існує загальнорекурсивна функція, що не входить в цей перелік.

Нехай y – перелік S, породжуючий послідовність а_о, А₁, А₂... всюди визначенних функцій.

Введемо функцію В(х)=А_х(х)+1. Оскільки Ах - загальнорекурсивна, то і В(х) загальнорекурсивна. Якщо ВÎS, то В має номер x_B і, отже,

B(x)=A_xB(x). (5.9)

Тоді в точці х=x_B за визначенням В(х_B)=А_хB(х_B)+1,а в силу (5.9) В(х_B)=А_хB(x_B). Отримуємо суперечність, звідки слідує, що В не входить в перелік, що породжується j.

Якщо ж в переліку допускаються часткові функції, то визначення В не приводить до суперечності, а означає лише, що в точці х_В В не визначена. З теореми 5.11 слідує вельми важливий результат.

Теорема 5.12. Проблема визначення загальнорекурсивності алгоритмів нерозв'язна; не існує алгоритму В(х), такого, що для будь-якого алгоритму Ах

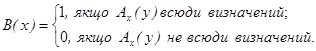
Нехай алгоритм В (х) існує; тоді він визначає загальнорекурсивну функцію f(х). Визначимо функцію g(х) таким чином:

g(0)=my[f(y)=1];

g(x+1)= my[y>g(x)&f(y)=1].

Оскільки номерів всюди визначених функцій (і, отже, точок у, в яких f(у)=1) нескінченна множина, то g(х) всюди визначена. Очевидно, що функція g з списку а_о, А₁, А₂.. всіх алгоритмів відбирає всі всюди визначені алгоритми, тобто є переліком множини всіх загальнорекурсивних функцій. З теореми 5.11 слідує, що такий перелік неможливий і, отже, алгоритму В(х), визначеного в умові теореми 5.12, не існує.

Теореми 5.4', 5.11 і 5.12 проливають світло на роль поняття часткової визначеності в теорії алгоритмів. Ще в § 5.1 серед вимог до алгоритмів говорилося про бажаність такої вимоги, як результативність алгоритму. Першим ударом по цій вимозі була нерозв'язність проблеми зупинки, що означає, що якщо алгоритм А може бути частковим, то за алгоритмом А і даним х не можна дізнатися, дасть А результат на даних х чи ні. Виникає природне бажання або взагалі прибрати часткові алгоритми із загальної теорії алгоритмів (скажімо, не вважати їх алгоритмами), або ввести стандартний метод довизначення часткових алгоритмів. Однак ні перше, ні друге ефективними методами зробити не можна. Перша ідея не годиться через теорему 5.12: немає ефективного способу розпізнавати часткові алгоритми серед множин всіх алгоритмів, і, отже, відбір, що пропонується, неможливий. Що ж до другої ідеї, то для неї є не менш переконливе спростування.

Теорема 5.13. Існує така частково-рекурсивна функція f, що ніяка загальнорекурсивна функція g не є її довизначенням. Визначимо f таким чином:

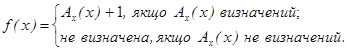
Як і раніше, передбачається, що зафіксована нумерація j і
j^-1(А_х)=х. Очевидно, що f(х) обчислювана. Нехай тепер g – довільна загальнорекурсивна функція і x_g – її номер: j^-1(g)=x_g. Оскільки g всюди визначена, то g(x_g) =A_xg(x_g) визначена і, отже, f(x_g) =g(x_g)+1. Таким чином, для будь-якої загальнорекурсивної функції g: f≠g в точці x_g.

Отже, існують часткові алгоритми, які не можна довизначати до всюди визначених алгоритмів.

Нарешті, ще одна ідея побудувати мову, що описує всі всюди визначені алгоритми і тільки їх, не може здійснитися тому, що описи в цій мові можна упорядити (наприклад, лексикографічно), і, отже, наявність такої мови означала б існування повного переліку всіх всюди визначених функцій, що суперечить теоремі 5.11. Таким чином, при формулюванні загального поняття алгоритму неминуче виникає дилема – або визначення алгоритму повинне бути досить загальним, щоб в число об'єктів, що задовольняють цьому визначенню, явно увійшли всі об'єкти, які природно вважати алгоритмами, або вимога про обов'язкову результативність алгоритму зберігається. У першому випадку цьому визначенню будуть задовольняти часткові алгоритми і позбутися них конструктивними методами не можна; у другому випадку ніяку процедуру не можна називати алгоритмом доти, поки для неї не буде розв’язана проблема зупинки, а єдиного методу розв'язання цієї проблеми не існує. У загальній теорії алгоритмів (для того, щоб вона дійсно була загальною) використовується перший варіант. Проте, ще раз зазначимо, що, коли мова йде про алгоритм, що вирішує дану задачу, теорія алгоритмів обов'язково вимагає сходимості (результативності), і тільки у випадку, коли алгоритм розв’язання всюди визначений, відповідна задача вважається вирішуваною. У цьому ж значенні використовується термін «вирішуваність» при введенні одного з найважливіших понять теорії алгоритмів - поняття вирішуваної множини.

Вирішувані і перечислимі множини. Множина М називається вирішуваною (або рекурсивною), якщо існує алгоритм A_m, який за будь-яким об'єктом а дає відповідь, належить а множини М чи ні. Алгоритм А_м називається дозволяючим алгоритмом для М.

Еквівалентне, але трохи більш точне визначення: множина М називається вирішуваною, якщо вона володіє загальнорекурсивною характеристичною функцією, тобто вичислимою всюди визначеною функцією c_M, такою, що

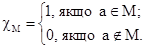
Наступне визначення зручніше дати відразу в функціональних термінах. Множина М називається перечислимою (або рекурсивно-перечислимою), якщо вона є областю значень деякої загальнорекурсивної функції, тобто, існує загальнорекурсивна функція y_M(x), така, що аєМ, якщо і тільки якщо для деякого х а=y_M(x). Функція y_M називається перечислимою для множини М; відповідно алгоритм, обчислюючий y_M (х), називається перечислимим або породжуючим для М.

Приклад 5.16

а) Множина квадратів натуральних чисел M{a|a=x²} перечислима (вона просто задана перелічуючою функцією a=x²)і вирішувана. Як дозволяючу процедуру можна запропонувати, наприклад, наступну: дане число а порівнюємо послідовно з 0, 1², 2²... і т.д. доти, поки не з'явиться таке число n², що або а=n², або а<n². В першому випадку аєМ, у другому - аÏМ.

б) Множина М_p, тобто множина всіх трійок цифр, що зустрічаються в десятеричному розкладанні p, перечислима. Перелічуюча процедура для неї полягає в послідовному обчисленні знаків розкладання p (один з алгоритмів їх обчислення відомий всім ще з шкільного курсу геометрії) і виписуванні трійок з послідовності, що виходить; для визначеної таким чином функції y_p маємо: y_p=314, y_p(1)=159, y_p(2)=265 і т.д. Деякі трійки можуть повторюватися, тому y_p – це приклад функції, що перелічує з повтореннями. Поки невідомо ніякого дозволяючого алгоритму для М_p, незважаючи на те, що очевидна кінцівка М_p! З іншого боку, це зовсім не означає, що М_p нерозв'язна; вона може виявитися і вирішуваною (наприклад, через досить велику кількість кроків перелічуючої процедури виявиться, що виписані всі можливі трійки від 000 до 999).

в) З індуктивних визначень, як правило, неважко витягнути породжуючу процедуру. Іноді вона міститься в них явно, як, скажімо, у визначенні (n+1)!=n!(n+1),що задає і перелічуючу функцію y(n)=n!, і спосіб її обчислення. Іноді, щоб отримати з такого визначення породжуючу функцію, треба ввести додаткові угоди. Наприклад, відоме індуктивне визначення PASCALю «ідентифікатор це або літера, або ідентифікатор, до якого праворуч приписана літера або цифра», породжує всі можливі в PASCALі ідентифікатори; однак для того, щоб надати цьому процесу породження вигляд перелічуючої функції, треба ввести порядок переліку. Якщо в якості такого порядоку прийняти лексикографічний і домовитися, що літери в ньому передують цифрам, то в алфавіті з 26 латинських букв і 10 цифр y(0)=а, y(25)=z, y(51)=az, y(54)=а2 і т.д. За допомогою аналогічних угод на основі індуктивного визначення формули можна побудувати перелічуючі функції для різних множин формул.

г) З попереднього прикладу видно, що перелічуюча функція, визначена на натуральному ряді, встановлює відповідність (не обов'язково взаємно однозначно) між числами і елементами множини, що породжується. Наприклад, ідентифікатору a_z відповідає число 51. Функція j, що нумерує алгоритми (тобто нумерація на стор. 202), встановлює відповідність між описами алгоритмів і числами, причому в нашому випадку відповідність взаємно однозначна. Тому можна сказати, що нумерація y, визначена на стор. 202, є перелічуючою функцією без повторень для множини всіх алгоритмів.

д) Множина всіх тотожно-істинних булевих формул вирішувана (наприклад, шляхом прямого обчислення на всіх наборах).

Важливість введених понять вирішуваності і перечислимости – передусім в тому, що завдяки їм стають точними такі поняття, як «конструктивний спосіб задання множини» і «множина, задана ефективно», які неформально обговорювалися ще в розд. 1. Зокрема, оскільки мова множин є універсальною мовою математики і всякому твердженню можна надати вигляд твердження про множини, мова вирішуваних і перечислимих множин є універсальною мовою для тверджень про існування (або відсутність) алгоритмів розв'язання математичних проблем. Наприклад, теорема 5.4 затверджує, що множина пар (х, у) таких, що алгоритм A_x при даних у дає результат, нерозв'язна, а теорема 5.12 - що нерозв'язна множина всіх загальнорекурсивних функцій.

Отже, ефективно задана множина - це множина, що володіє дозволяючою або перелічуючою функцією. Однак виникає питання, чи рівносильні ці два типи задання. В один бік відповідь майже очевидна.

Теорема 5.14. Якщо непуста множина М вирішувана, то вона перечислима.

Для визначеності будемо вважати, що М - це підмножина слів в алфавіті А. Нехай a₁, a₂,...,a_n... – перелік всіх слів в алфавіті А (наприклад, в лексикографічному порядку), b – деяке слово з М. Перечисляючу функцію y_M(n) для М визначимо так:

y_M(0)=b;

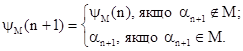
Ясно, що y_M(n) обчислювана і всюди визначена.

Звертання теореми 5.14 невірне.

Теорема 5.15. Існує множина М, яка перечислима, але нерозв'язна.

Доведемо, що такою є множина М={x|A_x(x) визначений}, тобто множина номерів самозастосовних алгоритмів. З теореми 5.9 слідує, що М нерозв'язна. Побудуємо перелічуючу функцію y_M для М. Будемо вважати для визначеності, що алгоритми - це машини Тьюрінга.

Таблиця 5.3

X	M
			...
	St(0, 0)	St(0, 1)	St(0, 2)	...
	St(1, 0)	...	...	...
	St(2, 0)	...	...	...
.
.	...	...	...	...
.

Введемо предикат St (х, m) - істинний, якщо машина з номером х при даних х зупиняється через m кроків. Очевидно, що цей предикат обчислимий і всюди визначений, для його обчислення треба запустити машину Тх при даних х і дати їй проробити m кроків.

Предикат St(х, m) можна представити у вигляді нескінченної квадратної матриці (таблиця 5.3), рядки якої відповідають першому аргументу х, стовпці - другому аргументу m, а в клітці (i, j), тобто на перетині i-й рядка і j-го стовпця, стоїть значення St(i, j). Упорядимо тепер клітки цієї матриці подібно тому, як упорядковувалася множина пар натуральних чисел в розд. 1 при доведенні її перечислимості: (0,0), (0, 1), (1, 0), (0,2), (1, 1), (2, 0), (0, 3)..., тобто спочатку клітки з сумою координат 0, потім клітки з сумою 1 і т. д. Тоді кожна клітка отримає номер, відповідний її порядку в цій послідовності. Виберемо яку-небудь явно самозастосовну машину Тьюрінга (наприклад, будь-яку всюди визначену машину з прикладів § 5.2), обчислимо її номер у введеній нумерації і позначимо його c. Визначимо тепер алгоритм обчислення функції y_M(n): знаходимо клітку (i, j) з номером n, якщо St(i,j)=І, то y_M(n)=i; якщо St(i, j)=П, то y_M(n)=с. Оскільки y_M(n)=i-це номер машини T_i, що зупиняється при даних i через j кроків, то область значень y_M містить тільки номери самозастосувальних машин. З іншого боку, всяка самозастосовувальна машина Тх зупиниться через кінцеве число k кроків; але тоді y_M(n')=х, де n' – це номер (х, k)_. Таким чином, область значень співпадає з множиною номерів самозастосовних алгоритмів; крім того, в зв'язку з загальнорекурсивністю предикату St функція y_M також загальнорекурсивна. Отже, вона є перелічуючою функцією для М.

Згідно з теоремою 5.15 перечислимість – більш слабкий вигляд ефективності; хоч перелічуюча процедура і задає ефективно список елементів множини М, однак пошук даного елемента а в цьому списку (завжди нескінченному, але, можливо, з елементами, що повторюються) може виявитися неефективним: це невизначено довгий процес, який зрештою зупиниться, якщо аєМ, але не зупиниться, якщо аÏМ. Тому список елементів М, заданий перелічуючою функцією, сам по собі не гарантує дозволяючої процедури для М, теорема 5.15 дає приклад, коли її просто не існує.

Проте, в одному важливому випадку перечислимість гарантує вирішуваність.

Теорема 5.16. М вирішувана тоді і тільки тоді, коли М і 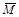перечислимі.

Дійсно, якщо М вирішувана, то також вирішуване 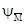=1-c_M, але тоді перечислимість М і виходить з теореми 5.14.

Нехай тепер М і 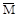перечислимі з функціями y_M і 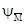відповідно. Але тоді для будь-якого елемента а його пошук в обох списках, точніше, в об'єднаному списку y_M(0), 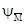(0), y_M(1), 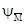(1)... обов'язково увінчається успіхом, оскільки або аÎМ, або аÏ 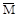. Такий пошук і є дозволяючою процедурою для М.

Зіставлення теорем 5.15 і 5.16 показує, що доповнення до перечислимої множини може виявитися неперечислимим; зокрема, множина несамозастосовуваних алгоритмів неперечислима. Така «несиметрія» самозастосування і несамозастосування пояснюється відміченою раніше несиметрією позитивної і негативної відповіді при пошуку заданого елемента в нескінченному списку: якщо A_x самозастосовуваний, то, обчислюючи А_х(х), ми про це коли-небудь дізнаємося; якщо ж Ах несамозастосовуваний, то про це не можна дізнатися, обчислюючи А_х(х).

Теорема Райса.

Розглядаючи накопичений запас алгоритмічно нерозв'язних проблем, неважко помітити, що майже всі вони так чи інакше пов'язані з самозастосовуваністю - досить екзотичною ситуацією, коли алгоритм працює з власним описом. Читач, що цікавиться прикладною теорією алгоритмів, може вирішити, що оскільки поняття самозастосування далеке від алгоритмічної практики, то нерозв'язність в цій практиці також ніколи не зустрінеться. Такого читача чекає гірке розчарування[1].

Теорема 5.17. (теорема Райса). Ніяка нетривіальна властивість обчислюваних функцій не є алгоритмічно вирішуваною.

Для доведення цю теорему зручніше сформулювати в менш ефектному, але більш точному вигляді: нехай С – будь-який клас обчислюваних функцій однієї змінної, нетривіальний в тому значенні, що є як функції, що належать С, так і функції, що не належать С. Тоді не існує алгоритму, який би за номером х функції f_x визначав би, належить f_x класу С чи ні; інакше кажучи, множина {x|f_xÎC} нерозв'язна.

Доведення. Припустимо, що множина M={x|f_xÎC} вирішувана; тоді воно має характеристичну функцію:

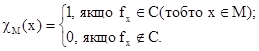
Нехай ніде не визначена функція. Виберемо яку-небудь конкретну обчислювану функцію f_aєM і визначимо функцію F(х, у):

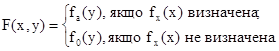
Функція F(х, у) обчислювана: для її обчислення треба обчислювати f_х(х); якщо f_x(х) визначена, то цей процес коли-небудь зупиниться і тоді треба перейти до обчислення f_a(у), якщо ж f_x(х) не визначена, то процес не зупиниться, що рівносильно обчисленню ніде не визначеної функції f₀(у). Якщо в F(х, у) зафіксувати х, то F стане обчислюваною функцією від однієї змінної у. Номер цієї функції залежить від значення х, тобто є всюди визначеною функцією g(х); неважко показати, що g(х) обчислювана. Отже,

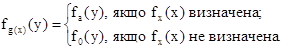
Отже, f_g(x)ÎM, якщо і тільки якщо f_x(х) визначена (оскільки f_aÎM, 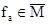).Звідси

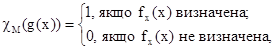
тобто побудована дозволяюча функція для проблеми самозастосування, що неможливо.

Для випадку, коли f_oÎM, вибираємо 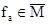; подальші міркування аналогічні, а дозволяюча функція для проблеми самозастосування буде мати вигляд: 1-c_M(g(x)).

З теореми Райса слідує, що за номером обчислюваної функції не можна дізнатися, чи є ця функція постійною, періодичною, обмеженою, чи містить вона серед своїх значень дане число і т.д. Створюється враження, що взагалі нічого не можна дізнатися і все на світі нерозв'язне. З другого боку, чи не суперечить теоремі Райса той очевидний факт, що за номером машини Т завжди можна дізнатися, наприклад, чи містить вона більше десяти команд чи ні?

Для того, щоб розібратися в значенні теореми Райса, треба передусім пригадати, що номер х функції f - це номер алгоритму А_х, обчислюючого f; в свою чергу, за номером алгоритму однозначно відновлюється його опис, і різним номерам відповідають різні алгоритми. Для функцій це є невірним: при х¹у f_x і f_y можуть бути однією і тією ж функцією (в її класичному значенні див. розд. 1). У теоремі Райса беруть участь і алгоритми, і функції, і їх потрібно чітко розрізнювати. Клас С – це клас (або властивість) функцій; в той же час «f_x» означає «функція, що обчислюється алгоритмом А_х». Таким чином, значення теореми Райса в тому, що за описом алгоритму нічого не можна дізнатися про властивості функції, яку він обчислює. Зокрема, виявляється нерозв'язною проблема еквівалентності алгоритмів: за двома заданими алгоритмами не можна дізнатися, обчислюють вони одну і ту ж функцію чи ні. Кількість же команд - це властивість не функції, а опису алгоритму; до теореми Райса вона не стосується.

Досвідченого програміста теорема Райса не повинна дивувати: він знає, що за текстом скільки-небудь складної програми, не запускаючи її в роботу, важко зрозуміти, що вона робить (тобто яку функцію обчислює), не маючи гіпотез про те, що вона повинна робити; якщо це розуміння і приходить, то кожний раз по-різному; систематичного методу тут не існує. З іншого боку, в цьому тексті можна виявити алгоритмічним шляхом так звані синтаксичні помилки (що і роблять компілятори з алгоритмічних мов), тобто виявляти ті або інші властивості опису алгоритму. Тут уперше варто згадати (поки неформально) два поняття, про які детальніше буде говоритися в двох наступних розділах, синтаксис і семантика. Синтаксичні властивості алгоритму - це властивості описуючих його текстів, тобто властивості кінцевих слів в фіксованому алфавіті. Семантичні (або смислові) властивості алгоритмів пов'язані з тим, що він робить; їх природно описувати в термінах функцій і класів еквівалентності функцій, що обчислюються алгоритмами. Добре відомо, що в процесі відладки програм синтаксичні помилки відшукуються досить швидко; всі прикрощі пов'язані з аналізом семантики неналагодженої програми, тобто з спробами встановити, що ж вона робить замість того, щоб робити задумане. У дещо вільній і неформальній інтерпретації теорема Райса могла б виглядати так: «за синтаксисом алгоритму нічого не можна дізнатися про його семантику».

Декілька разів повторюваний вираз «нічого не можна дізнатися» - це, строго кажучи, перебільшення. Його точний еквівалент «не існує єдиного алгоритму, що дозволяє дізнатися». До того ж мова йде про неможливість розпізнавання властивостей обчислюваних функцій, записаних в універсальній алгоритмічній мові (мові машин Тьюрінга та інш.). Властивості підкласів обчислюваних функцій, описаних в спеціальних мовах, цілком можуть виявитися вирішуваними. Наприклад, в розд.3 розглядалися алгоритми розпізнавання властивостей логічних функцій, описаних на мові формул в різних базисах.

Досі мова йшла про нерозв'язні проблеми всередині самої теорії алгоритмів. Деякі з них, такі, як проблема зупинки або теорема Райса, мають цілком реальну інтерпретацію в практиці програмування. Нерозв'язність виникає і в інших областях: в теорії автоматів, в теорії мов і граматик (див. розд. 7) і т.д. Поступово вони стають побутом дискретної математики, і з їх існуванням доводиться рахуватися. З теоретичної точки зору, нерозв'язність - не невдача, а науковий факт. Знання основної нерозв'язності теорії алгоритмів повинне бути для фахівця з дискретної математики таким же елементом наукової культури, як для фізика - знання про неможливість вічного двигуна. Якщо ж важливо мати справу з вирішуваною задачею (а для прикладних наук це прагнення природне), то потрібно чітко уявляти собі дві обставини. По-перше, відсутність загального алгоритму, що вирішує дану проблему, не означає, що у кожному окремому випадку розв'язання цієї проблеми не можна добитися успіху. Тому, якщо проблема нерозв'язна, треба шукати її вирішувані окремі випадки. По-друге, поява нерозв'язності - це, як правило, результат надмірної спільності задачі (або мови, на якій описані об'єкти задачі). Задача в більш загальній постановці має більше шансів виявитися нерозв'язною.

Контрольні запитання

1. Основні вимоги до алгоритмів.

2. Основні властивості алгоритмів.

3. Які можна виділити типи алгоритмів?

4. Що таке машина Тьюрінга?

5. Дані для машини Тьюрінга.

6. Що таке внутрішній і зовнішній алфавіти машини Тьюрінга?

7. Операції над машинами Тьюрінга.

8. Дайте визначення функції, обчислюваної за Тьюрінгом.

9. Що таке діаграма переходів машини Тьюрінга?

10. Що таке функціональна схема машини Тьюрінга?

11. Дайте визначення функціональної машини Тьюрінга.

12. Сформулюйте тезу Тьюрінга. Проблема зупинки.

13. Що таке алгоритмічна вирішуваність?

14. Дайте визначення рекурсивної функції. Що таке примітивна рекурсія?

15. Зв'язок рекурсивних функцій з машинами Тьюрінга. Теза Черча.

16. Обчислювальність і вирішуваність.

17. Наведіть формулювання теореми Райса.