Основні визначення

Машина Тьюрінга складається з:

1) керуючого пристрою, який може знаходитися в одному з станів, створюючих кінцеву множинуQ={q₁,..., q_n} (множина Q називається внутрішнім алфавітом);

2) стрічки, розбитої на клітки, в кожний з яких може бути записаний один з символів кінцевого алфавіта А={а₁,...a₂} (множинаА називається зовнішнім алфавітом);

3) пристрою звернення до клітки, тобто читаючої й пишучої голівки. Голівка в кожний момент часу оглядає клітку стрічки, в залежності від символа в цьому осередку і стану керуючого пристрою записує в клітку символ (можливо, співпадаючий з колишнім або пустим, тобто стирає символ), зсувається на клітку ліворуч або праворуч або залишається на місці; при цьому керуючий пристрій переходить в новий стан (або залишається в старому). Серед станів керуючого пристрою виділені початковий стан q₁ і заключний стан, який будемо позначати q_z. У початковому стані машина знаходиться перед початком роботи, попавши в заключний стан, машина зупиняється.

Таким чином, пам'ять машини Тьюрінга – це кінцева множина станів (внутрішня пам'ять) і стрічка (зовнішня пам'ять). Стрічка нескінченна в обидві сторони, однак в початковий момент часу тільки кінцеве число кліток стрічки заповнене непустими символами, інші клітки пусті, тобто містять пустий символ l (пропуск), він може бути позначений і іншими символами, наприклад, Ù або Ú. З характеру роботи машини слідує, що в будь-який подальший момент часу лише кінцевий відрізок стрічки буде заповнений символами. Тому важлива не фактична (як кажуть в математиці, актуальна) нескінченність стрічки, а її необмеженість, тобто можливість писати на ній як бажано довгі, але кінцеві слова. Дані машини Тьюрінга - це слова в алфавіті стрічки; на стрічці записуються і початкові дані, і остаточні результати. Елементарні кроки машини - це читання і запис символів, зсув голівки на клітку ліворуч і праворуч, а також перехід керуючого пристрою в наступний стан. Детерминованість машини, тобто послідовність її кроків, визначається таким чином: для будь-якого внутрішнього стану q_i і символа a_j однозначно задані:

а) наступний стан q_j'; б) символ а_j', який треба записати замість а_j в ту ж клітку (стирання символа будемо розуміти як запис пустого символа); в) напрям зсуву голівки d_ij, що означається одним з трьох символів: L (ліворуч), R (праворуч), Е (на місці). Це завдання може описуватися або системою правил (команд), що мають вигляд:

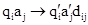, (5.1)

або таблицею, стовпцям якої відповідають стани, рядкам - вхідні символи, а на перетині рядка q_i і стовпця a_j записана трійка символів 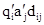, (така таблиця називається функціональною схемою), і нарешті, блок-схемою, яку будемо називати діаграмою переходів. У цій діаграмі станам відповідають вершини, а правилу виду (5.1) - ребро,що веде з q_i в 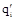на якому написано: 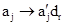. Умова однозначності вимагає, щоб для будь-якого j і будь-якого i¹z в системі команд була одна команда, аналогічна (5.1), з лівою частиною q_ia_j; стан q_z в лівих частинах команд не зустрічається. На діаграмі переходів це виражається умовою, що з кожної вершини, крім q_z, вийдуть точно m ребер, причому на різних ребрах ліві частини різні; у вершини q_z немає ребер, що виходять. 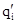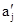Надалі домовимося опускати символи і ,якщо , .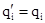

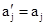Повний стан машини Тьюрінга, за яким однозначно можна визначити її подальшу поведінку, визначається її внутрішнім станом, станом стрічки (тобто словом, записаним на стрічці) і положенням голівки на стрічці. Повний стан будемо називати конфігурацією, або машинним словом, і означати трійкою a₁q_ia₂, де q_i – поточний внутрішній стан, a₁ - слово зліва від голівки, а a₂ - слово, утворене символом, що оглядається голівкою, і символами праворуч від нього, причому зліва від a₁ і праворуч від a₂ немає непустих символів. Наприклад, конфігурація з внутрішнім станом q_i, в якій на стрічці записане abcde, а голівка оглядає d, запишеться як abcq_ide. Стандартною початковою конфігурацією назвемо конфігурацію виду q₁a, тобто конфігурацію, що містить початковий стан, в якій голівка оглядає крайній лівий символ слова, написаного на стрічці. Аналогічно стандартною заключною конфігурацією назвемо конфігурацію виду q_za. До всякої незаключної конфігурації К машини Т застосовна лише одна команда виду (5.1), яка К переводить в конфігурацію К'. Ці відносини між конфігураціями визначимо 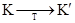; якщо з контексту ясно, про яку машину Т йде мова, індекс Т будемо опускати. Якщо для K₁ і K_n існує послідовність конфігурацій K₁, K₂,..., K_n така, що 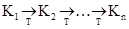, визначимо це 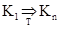. Наприклад, якщо в системі команд машини Т є команди q₂a₅®q₃a₄R і q₃a₁L®q₄a_2, то q₂a₅a₁a₂®a₄q₃a₁a₂®q₄a₄a₂a₂ і, отже, q₂a₅a₁a₂Þq₄a₄a₂a₂. Послідовність конфігурацій 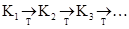однозначно визначається початковою конфігурацією K₁ і повністю описує роботу машини Т, починаючи з K₁. Вона кінцева, якщо в ній зустрінеться заключна конфігурація, і нескінченна в іншому випадку.

Приклад 5.3. Машина із зовнішнім алфавітом А={1, l}, внутрішнім алфавітом {q₁, q_z} і системою команд q₁1®q₁1R, q₁l®q₁1R з будь-якої початкової конфігурації буде працювати нескінченно, заповнюючи одиницями всю стрічку праворуч від початкової точки.

Приклад 5.4. Для будь-якої машини Т, якщо K₁ 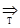K_i 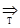K_j і K_i=K_j, послідовність K₁ÞK_iÞK_jÞ... є нескінченною: її відрізок K₁ÞK_j буде повторюватися (зациклюватися).

Якщо a₁q₁a₂Þb₁q_zb₂, то будемо говорити, що машина Т переробляє слово a₁a₂ в слово b₁b₂, і означати це T(a₁a₂)=b₁b₂. Запис Т(a) іноді будемо вживати і в іншому значенні: просто як позначення машини Т з початковими значеннями a.

Для того, щоб говорити про те, що можуть робити машини Тьюрінга, необхідно уточнити, як буде інтерпретуватися їх поведінка і як будуть представлятися дані. Початковими даними машини Тьюрінга будемо вважати записані на стрічці слова в алфавіті початкових даних A_вих(A_вих ÍА) і вектори з таких слів (словникові вектори над A_вих). Це означає, що для кожної машини будуть розглядатися тільки ті початкові конфігурації, в яких на стрічці записані словникові вектори над A_вих. Запис на стрічці словникового вектора (a₁,..., a_r) назвемо правильним, якщо він має вигляд a₁la₂l...a_r-1la_r (при умові, що lÏA_вих) або a₁*a₂*…a_r-1*a_r, де * – спеціальний символ-роздільник, що не входить в A_вих. Для будь-якого вектора V_ісх над А_ісх машина Т або працює нескінченно, або переробляє його в сукупність слів (розділених пропусками) в алфавіті, який назвемо алфавітом результатів і визначимо А_рез; A_вих і А_рез можуть перетинатися і навіть співпадати. В ході роботи на стрічці можуть з'являтися символи, що не входять в A_вих і А_рез і створюють проміжний алфавіт А_пр (що утримує, зокрема, роздільник). Таким чином, алфавіт стрічки А=A_вихÈА_резÈА_пр. В найпростішому випадку A_вих =А_рез и А= A_вих È{l}.

Нехай f – функція, що відображає множину векторів над A_вих в множину векторів над А_рез. Машина Т правильно обчислює функцію f, якщо: 1) для будь-яких V і W таких, що f(V)=W, q₁V* 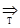q_zW*, де V* і W* -правильні записи V і W відповідно; 2) для будь-якого V, такого, що f(V) не визначена, машина Т, запущена в стандартній початковій конфігурації q₁V*, працює нескінченно. Якщо для f існує машина Т, яка її правильно обчислює, функція f називається правильно обчислюваною за Тьюрінгом.

З іншого боку, всякій правильно обчислюючій машині Тьюрінга, тобто машині, яка, почавши зі стандартної початкової конфігурації q₁a, може зупинитися тільки в стандартній заключній конфігурації q_za, можна поставити у відповідність функцію, що обчислюється нею. Дві машини Тьюрінга з однаковим алфавітом A_вих будемо називати еквівалентними, якщо вони обчислюють одну і ту ж функцію. Зокрема, машини з прикладів 3 і 4 еквівалентні, оскільки вони обчислюють одну і ту ж ніде не визначену (пусту) функцію.

Приклад 5.5. Якщо машина Т містить команди q_ja_j®q_i^'a_j^'E и q_i^'a_j^'®q_i^''a_j^''d_r, то, замінивши ці дві команди командою q_ia_j®q_i^''a_j^''d_r, отримаємо машину Т', еквівалентну Т. Шляхом таких перетворень можна в машині Т прибрати всі команди, що містять Е, для випадку, коли q_i' – не заключний стан; при цьому може скоротитися число станів (деякі q_i' не увійдуть в праві частини нових команд і стануть недосяжними з q₁). Якщо q_i' – заключний стан, то, ввівши новий заключний стан q_n+1 і замінивши команду q_ia_j®q_i^'a_j^'E на m+1 команду q_ia_j®q_i^'a_j^'R, q_i^'a₁®q_n+1a₁L,..., q_i^'a_m®q_n+1a_mL (m – число літер в А), отримаємо машину, також еквівалентну Т. Таким чином, для будь-якої машини Т існує еквівалентна їй машина, що не містить в командах Е; тому можна розглядати машини, голівки яких на кожному кроці рухаються.

Визначення, пов'язані з обчисленням функцій, заданих на словникових векторах, дані з явним «запасом спільності» і мають на увазі переробку нечислових об'єктів. Надалі це знадобиться; однак найближчим часом будуть розглядатися числові функції, точніше, функції, що відображають N в N. Домовимося представляти натуральні числа в одиничному (унарному) коді, тобто для всіх числових функцій A_вих ={1} або A_вих ={1, *}, і число х представляється словом 1...1=1^х, що складається з х одиниць. Таким чином, числова функція f(x₁,...x_n) правильно обчислювана за Тьюрінгом, якщо існує машина Т, така, що q₁ 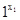* *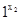... 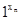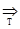q_z1^y, коли f(x₁...x_n)=у, і Т працює нескінченно, починаючи з q₁ 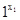* *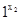... 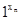, коли f(x₁...x_n) не визначена.

Почавши з досить загальних визначень абстрактних машин, ми потім ввели при визначенні обчислень на цих машинах ряд обмежень, пов'язаних з правильним записом, правильним обчисленням, представленням чисел у вельми неощадливому одиничному коді і т.д. Чи не втрачається при цьому спільність? Дійсно, можливі інші визначення обчислення: наприклад, можна в заключній конфігурації допускати символи з проміжного алфавіта А_пр, а результатом вважати слово в А_рез, яке вийде, якщо символи з А_пр викинути і «зсунути» шматки, що залишилися. Зокрема, якщо А_рез={1}, то результатом буде число,що дорівнює числу одиниць на стрічці в заключній конфігурації. Виявляється, що втрати спільності не відбувається; зокрема, якщо функція обчислювана в останньому значенні, то вона правильно обчислювана. Не будемо займатися детальним доведенням цього твердження в загальному вигляді, однак проілюструємо його справедливість на прикладах. Тому звичайно прикметник «правильний» будемо опускати і говорити просто про функції, обчислювані за Тьюрінгом.

Приклад 5.6. а). Складання. У введеному раніше представленні чисел скласти числа а і b - це означає слово 1^a * 1^b переробити в слово 1^a+b, тобто видалити роздільник * і зсунути один з доданків, скажімо перший, до іншого. Це перетворення здійснює машина Т₊ з чотирма станами і наступною системою команд (перша команда введена для випадку, коли а=0, і початкове слово має вигляд *1^b):

1. q₁*®q_zlR;

2. q₁1®q₂lR;

або функціональною схемою:

Таблиця 5.2

q21®q2lR;		q1	q2	q3
q2*®q31L;	*	qzlR	q31R
q31®q31L;		q2lR	q2lR	q31L
q3l®qzlR.	l			qzlR

У цій системі команд перераховані не всі поєднання станів машини і символів стрічки: опущені ті з них, які при стандартній початковій конфігурації ніколи не зустрінуться. Опускати непотрібні команди будемо надалі; в таблицях це буде позначено прочерками. Діаграма переходів Т+ наведена на мал. 5.4; заключний стан познаічений подвійним колом.

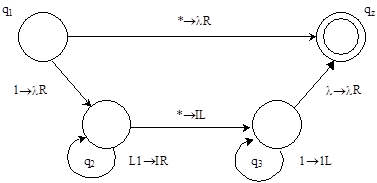
Мал. 5.4.

б). Копіювання (перезапис) слова, тобто переробка слова a в a*a. Для чисел цю задачу вирішує машина Т_коп, система команд якої наведена в табл. 5.3.

Таблиця 5.3

	q1	q2	q3	q4
	q20R	q21R	q31R	q41L
l	qzlR	q3*R	q41L
*	q1*L	q3*R		q4*L
	q11L			q10R

Діаграма переходів Т_коп дана на мал. 5.5. На цій діаграмі (а також подальших) прийняті скорочення: 1) якщо з q_i в q_j ведуть два ребра з однаковою правою частиною, то вони об'єднуються в одне ребро, на якому ліві частини записані через кому; 2) якщо символ на стрічці не змінюється, то він в правій частині команди не пишеться. На петлі в q₄ використані одночасно обидва скорочення.

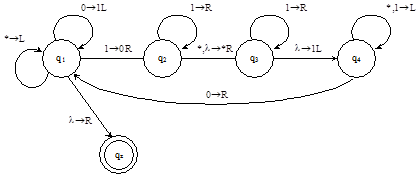
Мал. 5.5.

Машина Т_коп при кожному проході початкового числа 1^a замінює ліву з його одиниць нулем і пише (в стані q₃) одну одиницю праворуч від 1^a в найближчу пусту клітку. При першому проході, крім того, в стані q₂ ставиться маркер. Таким чином, копія 1^a будується за a проходів. Після запису чергової одиниці машина переходить в стан q₄, який пересуває голівку ліворуч від найближчого нуля, після чого машина переходить в q₁ і цикл повторюється. Він переривається, коли q₁ виявляє на стрічці не одиницю, а маркер. Це означає, що всі одиниці 1^a вичерпані, тобто зроблено a проходів. Тоді голівка повертається ліворуч в своє початкове положення, замінюючи по дорозі всі нулі одиницями.

Приклад 5.7. Сконструюємо машину Тьюрінга для знаходження суми чисел, заданих не в унарному коді, а в різних системах числення. Наприклад, знайдемо суму числа, заданого в троїчній системі, і числа, заданого у восьмиричній системі. Очевидно, що зовнішній алфавіт машини Тьюрінга А={0,1,2,3,4,5,6,7,+,l}, внутрішній алфавіт Q={q₁, q₂, q₃, q₄, q₅}.

Нехай доданки розділяються знаком +, пусті секції, як і раніше, означаються l, нехай на стрічці зліва від знаку + розташовано доданок у восьмиричному коді, праворуч - доданок в троїчному коді. Ідея розв’язання задачі полягає в наступному: від числа, розташованого праворуч, віднімаємо одиницю, діючи за правилами троїчної арифметики, потім просуваємося ліворуч і до восьмиричного числа додаємо одиницю, діючи за правилами восьмиричної арифметики. Після цього повертаємося до правого числа і повторюємо все доти, поки доданок, розташований праворуч від знаку +, не буде вичерпаний.

Після цього останній раз зсуваємося праворуч, стираємо знак + і робимо зупинку. Функціональна схема таблиці Тьюрінга представлена в таблиці 5.4.

Таблиця 5.4.

	q1	q2	q3	q4	qs
	q12L	L	q41R	R
	q20L	L	q42R	R
	q21L	L	q43R	R	q5lR
			q44R	R
			q45R	R
			q46R	R
			q47R	R
			q30L	R
+	q5lR	q3L		R
l			q41R	q1l	qz

Побудовану машину Тьюрінга можна використати як троїчно-восьмиричний дешифратор.