Психолого-педагогические основы преподавания задач на построение

Геометрия имеет огромный развивающий и образовательный потенциал, чем и привлекает внимание многих методистов, педагогов и даже, как ни странно звучит, психологов. Содержание линии задач на построение, ее структура, соотношение в ней логического и интуитивного, и многие другие вопросы заслужили пристального внимания.

Как мы знаем, развитие ученика средствами предмета – это одна из основополагающих задач преподавания как геометрии, так и других учебных предметов. Но, к сожалению, стоит заметить, что зачастую эффективность реального обучения школьников не достигает уровня требований, предъявляемых обществом к качеству знаний учащихся, к интеллектуальным свойствам личности и степени сформированности определенных умений и навыков школьников.

Данная картина обусловлена рядом объективных и субъективных причин. В психолого-педагогической и методической литературе чаще всего называют следующие:

1) отсутствие у школьников потребности в дедуктивном доказательстве геометрических фактов;

2) недостаточная геометрическая подготовка учащихся;

3) медленная мыслительная деятельность;

4) неразработанность отдельных вопросов методики преподавания геометрии.

В дальнейшем это приводит к ряду проблем, а именно к тому, что учащиеся:

1) могут решать только элементарные задачи;

2) совершают множество ошибок при измерении геометрических величин;

3) не могут анализировать заданную конфигурацию;

4) не могут решать задачи, связанных с выполнением практических измерений.

Умение рассуждать логически и убедительно имеет огромное значение не только в планиметрии, но и в нашей повседневной жизни. В применении к планиметрии это означает, что учащиеся должны уметь доказывать. Приобщение школьников к логическим доказательствам является одной из наиболее сложных методических проблем. Учащиеся не понимают необходимости обладания дедуктивными навыками. Особенности планиметрических задач на доказательство при объяснении материала создают в сознании учащихся психологический барьер. Но намного серьёзнее возникают трудности при самостоятельном доказательстве утверждений из-за слишком маленького личного опыта в построении логических доказательств. Школьник не знает что, не знает зачем, и не знает как доказывать. Успех выполнения таких задач случаен.

Наиболее важным этапом в обучении решения задач на доказательство является формирование внутренней потребности в логических обоснованиях. Брадис В.М., Рогановский Н.М., Сикорский А.П и другие считают, что данная проблема может быть решена на первых уроках планиметрии и предлагают систему упражнений, мало связанных или совсем не связанных с изучаемым материалом.

Необходимость целенаправленной работы по формированию у школьников приемов работы с чертежом на начальном этапе изучения геометрии выделялась в работах известных педагогов, методистов, психологов. А именно, Владимирским Г.А., Добровольским В.В., Кабановой-Меллер Е.Н., Ломовой Б.Ф., Протасовой И.Ф. и др. Процесс формирования и развития умения работать с чертежом ни в коем случае нельзя связывать с изучением одной лишь определенной темы или группы тем. Поэтому этот процесс должен быть организован на протяжении всего курса геометрии при изучении любой темы.

Но нельзя забывать, что геометрический чертеж при неправильном его использовании может оказать и тормозящее воздействие.

У школьников возникают затруднения в распознавании геометрических фигур:

1) при включении их в некоторую геометрическую конфигурацию;

2) при их нестандартном расположении на плоскости;

3) при определении взаимного расположения геометрических фигур и их элементов.

Согласно мнению психологов, знание эффективнее усваивается учащимися во время специально организованной деятельности, когда они выполняет самостоятельно большую часть действий. Стандартная же методика преподавания планиметрии использует методы обучения, при которых работа учащихся сводится к воспроизведению слов учителя или пересказу содержания учебника.

Среди теорем учебников по геометрии есть такие, которые школьники могут самостоятельно доказать, пользуясь при этом ранее полученными знаниями. Но, к сожалению, на практике самостоятельные работы организуются крайне редко.

Также необходимо не забывать, что у учащихся 13 - 15 лет абстрактное мышление достаточно развито, но все же они предпочитают конкретную деятельность, а не теорию. Поэтому при изложении курса планиметрии в каждой теме нужно находить время для практики. Действия учащихся должны приводить к гипотезам, подтверждающимся в скором времени логическим путем.

По мнению видных психологов и педагогов, таких как Давыдов В.В., Зак А.З., Кулюткин Ю.Н., Семенов И.Н., важную роль играет для развития мышления учащихся и рефлексии. Для того чтобы подготовить способных к самостоятельным изысканиям людей, нужно рассматривать задачи, приучающие к критическому анализу условий, а именно, задачи, условия которых не определяют объектов. Огромным минусом является то, что учащиеся привыкают к тому, что в задаче имеются лишь необходимые для решения данные. Таким образом, моделируются ситуации, не соответствующие реальности. В повседневной жизни никто заранее не отбирает необходимые данные. В данном случае у школьников не вырабатываются правила работы с новыми задачами, не формируются навыки самоконтроля и самоанализа учебной деятельности. Учащиеся просто заучивают факты, не понимают логику построения доказательств теорем, и, следовательно, не смогут самостоятельно решить планиметрическую задачу

2.Методика решения задач на построение

При решении сложных задач основную трудность представляет вопрос о том, как найти способ решения. Решение этого вопроса облегчается, если придерживаться определенной схемы рассуждений.

1. Анализ. В анализе ведется поиск решения задачи следующим образом: предполагают задачу решенной, строят (от руки) искомую фигуру пристраивают к ней данные с учетом тех отношений, которые указаны в условии задачи. Подмечают, что построение искомой фигуры Ф сводится к построению другой фигуры Ф₁, построение Ф₁ сводят к построению Ф₂ и т.д. После конечного числа шагов можно прийти к некоторой фигуре Ф_n, построение которой известно.

Если на вспомогательном чертеже не удастся найти ход решения, то целесообразно ввеcти в чертеж вспомогательные фигуры: сделать дополнительные построения, сделать геометричеcкие преобразования и т.д.

2. Построение состоит в указании конечной последовательности основных построений (или ранее решенных задач), которые достаточно произвести, чтобы искомая фигура была построена.

Построение обычно сопровождается графическим оформлением каждого шага с помощью указанных инструментов.

3. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет условию задачи.

Доказательство проводится в предположении, что каждый шаг построения может быть выполнен.

4. Исследование. При анализе, построении обычно ограничиваются отысканием одного какого-либо решения, предполагая выполнимость шагов построения. Идя полного решения задачи нужно выяснить:

1) всегда ли можно выполнить построения избранным способом;

2) можно ли и как построить искомую фигуру, если для какого-нибудь выбора данных указанный способ построения не пригоден;

3) сколько решений имеет задача при каждом возможном выборе данных.

Эти вопросы составляют содержание исследования. Итак, исследование ставит цель - установить условия разрешимости и определить число решений.

Однако такое исследование связано с данным способом построения. В этом случае остается открытым вопрос: нет ли других решений при другом способе решения. На этот вопрос отвечают с помощью указанного выше приема: доказывают, что произвольное решение данной задачи совпадает с одним из уже полученных решений.

Задача. Построить треугольник, если известны: длина основания а, угол при основании α и разность двух других сторон d.

Решение. Заметим, что в условии задачи не указаны инструменты. B таких случаях будем полагать, что задачу надо решить с помощью линейки и циркуля.

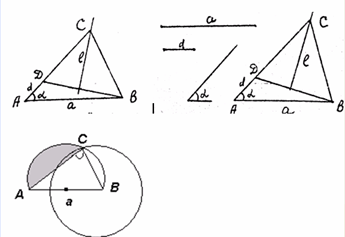
Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD = d, 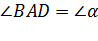. ∆АВD определен по двум сторонам и углу между ними.

Третья вершина С искомого треугольника может быть найдена как точка пересечения луча АD и прямой l - серединного перпендикуляра отрезка ВD. План решения найден, отроим треугольник ∆АВD, а затем и третью вершину С.

Построение. В этом пункте реализуем план решения.

Строим последовательно:

1)

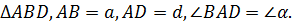
2) l, l – серединный перпендикуляр отрезка BD.

3) C, C = [AD) ∩ l.

Треугольник АВС – искомый.

Доказательство. Действительно, ∆АВС удовлетворяет всем условиям задачи, т.к. по построению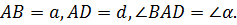

Исследование. Проверим каждый шаг построения на осуществимость и единственность. Первый шаг возможен и единственен тогда и только тогда, когда 0<α<π. Второй шаг возможен и единственен всегда. Третий шаг возможен и единственен тогда и только тогда, когда α< а cos α. Действительно, если d < a cos α, то прямая l пересекает луч AD. Если же d = a cos α, то l и AD, поэтому треугольника, удовлетворяющего условию задачи, не существует. В том случае, когда d < a cos α, прямая l пересекает луч DА. В этом случае также задача не имеет решения.

Но вернемся к анализу. У нас задача решена, предполагая, что α лежит против меньшей из двух боковых сторон. Если α лежит против большей стороны, то предыдущий метод построения не проходит. Как быть? По теории мы должны и для этого случая дать решение. Нетрудно убедиться, что ΔABF определен (a,d и угол π - α). Построение, доказательство и исследование провoдятcя так же, как и выше.

Необходимо еще выяснить: вcе ли решения найдены. Да, все, так как если бы каким-то способом построить треугольник по a, d и α то этот треугольник был бы равен одному из указанных треугольников.

ЗАКЛЮЧЕНИЕ

Существует множество различных мнений о месте геометрии, в частности и планиметрии, о ее месте в системе школьного образования, но все они сходятся в том, что недостатки в освоении геометрии ведут к ущербу всего миропонимания.

Геометрические образы сопровождают человека с первых лет и до конца жизни. Они появляются еще до того, как он их формально- логически осмыслит. Чем многограннее мир ребенка, тем большее число подобных первоначальных знаний он получает до начала обучения в учебном учреждении. Как заметили, учителя и специалисты-психологи, при неверном обучении наличие способностей к оперированию геометрическими образами и синтезированию геометрических знаний может в дальнейшем не развиться или же резко ослабнуть. Именно из-за этого планомерное и систематическое развития образного мышления, восприятие геометрии как феномена человеческой культуры - одна из главных задач преподавания геометрии.

Планиметрические задачи традиционны для курса геометрии. Эти задачи по своим методам решения улучшают способность представлять себе геометрические фигуры и учат нас мысленно оперировать элементами этой фигуры. Задачи на построение способствуют пониманию возможности преобразования геометрических фигур, что, в свою очередь, сказывается на пространственном мышлении школьников. Планиметрические задачи развивают геометрическую интуицию и логическое мышление. Преподаватель может эффективно формировать элементы алгоритмической культуры школьников во время решения этих задач. С помощью планиметрических задач:

1) готовят к самостоятельным исследованиям, что не маловажно в условиях формировании умений и навыков умственного труда.

2) развивают внимание, дисциплинированность, настойчивость и целеустремленность, изобретательность, инициативу, трудолюбие.

ЛИТЕРАТУРА

1) Александров, И.И. Сборник геометрических задач на построение с решениями. – М.: Учпедгиз,1954.

2) Белошистая, А.В. Задачи на построение в школьном курсе геометрии// Математика в школе. – 2002. – №9.

3) Жохов В.И., Крайнева Л.В., Карташова Г.Д. Геометрия, 7-9. Кн. для учителя. М.: Просвещение, 2004.

4) Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ВятГГУ, 2008.

5) Орленко М.И. Решение геометрических задач на построение в курсе математики средней школы, Минск, 1953

6) Петерсон К., Методы и теория решения геометрических задач на построение с приложением более 400 задач. - Харьков: Книжный магазин Корвин и К, 1883.

7) Понарин, Я.П. Элементарная геометрия: В 2 т. – Т.1: Планиметрия, преобразования плоскости / Я.П.Понарин. – М.: МЦНМО, 2004.

8) Саранцев, Г.И. Обучение математическим доказательствам и опровержениям в школе / Г.И. Саранцев. – М.: ВЛАДОС, 2005.

9) Столяренко Л.Д., Педагогическая психология: серия «Высшее образование» / Л.Д. Столяренко. – 3-е изд., перераб. И доп. – Ростов н / Д: «Феникс», 2004.

10) Фридман Л.М. Психолого-педагогические основы обучения в школе / Фридман Л.М. – М.: Просвещение, 1983.