Глава 1. Теория геометричческих построений

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ (РИНХ)»

ТАГАНРОГСКИЙ ИНСТИТУТ ИМЕНИ А.П.ЧЕХОВА

(филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ростовский государственный экономический университет (РИНХ)»

ФАКУЛЬТЕТ ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАТИКИ

КАФЕДРА МАТЕМАТИКИ

МЕТОДИКА ФОРМИРОВАНИЯ УМЕНИЙ РЕШАТЬ ОСНОВНЫЕ ЗАДАЧИ НА ПОСТРОЕНИЕ В КУРСЕ ПЛАНИМЕТРИИ.

Курсовая работа

по методике обучения математики

студентки 3 курса, очная форма обучения

Карсуковой Анастасии Александровны

Педагогическое образование

Профили «Математика» и «Физика»

Научный руководитель:

кандидат пед. наук, доцент

Дяченко Светлана Иосифовна

Дата сдачи «____»_______2015г.

Дата защиты «____» ______2015г.

Оценка____________

Научный руководитель_______________/_______________/

Таганрог

ВВЕДЕНИЕ……………………………………………………………………..3-4

ГЛАВА 1. ТЕОРИЯ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ В ШКОЛЕ

1. Основные аксиомы конструктивной геометрии……………...…..5-8

2. Задача на построение…………………………………...……………...…9-10

3. Методы решения задач на построение………………………….11-13

4. Задачи на построение в системе задач школьного курса геометрии…………………………………………………………...14-18

ГЛАВА 2. РЕШЕНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ

1. Психолого-педагогические основы преподавания задач на построение………………………………………………………………19-22

2. Методика решения задач на построение…………..……………23-25

ЗАКЛЮЧЕНИЕ………………………………………………………………..26

ЛИТЕРАТУРА…………………………………………………………………..27

ВВЕДЕНИЕ

Основополагающей целью современного математического образования в любом среднем образовательном учреждении считается воспитание математической культуры школьников. Имеется в виду не механическая передача детям основного объема математических знаний, умений и навыков, а становление у них математического склада ума. Прежде всего, учащихся необходимо обучать методам и приемам математической деятельности, а также воспитывать у них устойчивый интерес к познанию математического мира. Основным инструментом повышения уровня математической подготовки школьников считается их непосредственная деятельность по решению математических задач. Особую роль выполняют планиметрические задачи. Они обеспечивают целенаправленное усвоение содержания конструктивного компонента умственной деятельности в области геометрии.

Во время решения планиметрических задач обнаруживаются связи между всеми компонентами когнитивной деятельности. Возможность широкого выбора методов и способов решения является характерной чертой таких задач. В границах традиционной методики обучения математике решение планиметрических задач является решением подзадач большинства геометрических задач. А именно, задач на вычисление и на доказательство. Очевидно, что решить планиметрическую задачу школьного курса невозможно без каких-либо геометрических построений.

Значительное число видных, как зарубежных, так и отечественных, математиков и методистов посвятило свои работы исследованию вопросов постановки и обучения решению задач на построение. Например, Адамар Ж., Александров И.И., Далингер В.А., Никитин Н.Н., Саранцев Г.И., Семушин А.Д., Фуше А., Шохор-Троцкий С.И. и др.

Исследованием и построением теории и методики обучения решению математических задач занимались Глейзер Г.Д., Гусева В.А., Зайкин М.И., Колягин Ю.М., Крупич В.И, Луканкин Г.Л., Смирнова И.М., Столяр А.А., Цукарь А.Я., Шарыгин И.Ф. и многие другие.

К сожалению, на данный момент изучение задач на построение в школьном курсе геометрии носит эпизодический характер.

Актуальность данной курсовой работы определяется наличием противоречия между большой психолого-педагогической значимостью планиметрических задач с точки зрения их содержания и особенностей процесса их решения, а также недостаточным вниманием к ним в современном обучении геометрии.

Цель данной курсовой работы заключается в изучении и систематизации методики обучения учащихся средних общеобразовательных школ решению планиметрических задач, что в дальнейшем поможет в разработке новой методики, у которой будет усилена имеющаяся содержательно-методическую планиметрическая линия школьного курса геометрии.

Объектом исследования курсовой работы является процесс обучения школьников геометрии в основной школе.

Предметом исследования является процесс формирования конструктивных умений учащихся, необходимых при решении планиметрических задач.

Для достижения обозначенной выше цели необходимо решить следующие задачи:

1) обосновать педагого-психологические и методико-дидактические основы формирования конструктивных умений учащихся, необходимых для решения планиметрических задач;

2) рассмотреть методы решения задач на построение;

3) выяснить место задач на построение в школьном курсе геометрии.

ГЛАВА 1. ТЕОРИЯ ГЕОМЕТРИЧЧЕСКИХ ПОСТРОЕНИЙ

1. Основные аксиомы конструктивной геометрии.

Фигурой в геометрии называют любую совокупность точек, содержащую по крайней мере одну точку.

Будем предполагать, что в пространстве дана некоторая плоскость, которую назовём основной плоскостью. Ограничимся рассмотрением только таких фигур, которые принадлежат этой плоскости.

Примерами фигур могут служить:

· точка;

· пара точек;

· прямая (рассматриваемая как совокупность принадлежащих ей точек);

· пара параллельных прямых; отрезок (фигура, состоящая из двух точек и всех точек прямой, лежащих между ними);

· интервал, или открытый отрезок (совокупность всех точек, лежащих между двумя данными точками прямой);

· луч (фигура, состоящая из некоторой точки прямой и всех точек этой прямой, расположенных по одну сторону от этой точки);

· окружность (совокупность всех точек плоскости отстоящих на данное расстояние от некоторой данной точки этой плоскости);

· круг (совокупность всех точек плоскости, расстояния которых от данной в этой плоскости точки не превышают длины данного отрезка) и др.

Одна фигура называется частью другой фигуры, если каждая точка первой фигуры принадлежит второй фигуре. Так, например, частями прямой будут: всякий лежащий на ней отрезок, лежащий на этой прямой луч, точка на этой прямой, сама прямая.

Соединением двух или нескольких фигур называется совокупность всех точек, принадлежащих хотя бы одной из этих фигур. Соединение фигур Ф₁ и Ф₂ обозначают так: Ф₁ + Ф₂ или Ф₁ υ Ф₂.

Пересечением, или общей частью двух или нескольких фигур, называется совокупность всех точек, которые являются общими для этих фигур. Пересечение двух фигур Ф₁ и Ф₂ обозначают так: Ф₁·Ф₂ или Ф₁ ∩ Ф₂.

Пример. Если расстояние прямой от центра окружности меньше радиуса этой окружности, то пересечение прямой с окружностью представляет пару точек. Если расстояние прямой от центра окружности равно радиусу окружности (случай касания), то пересечением будет одна точка (точка касания).

Разностью двух фигур Ф₁ и Ф₂ называется совокупность всех таких точек фигуры Ф₁, которые не принадлежат фигуре Ф₂. Разность фигур Ф₁ и Ф₂ обозначается так: Ф₁\Ф₂. Например, разность между прямой и лежащим на ней интервалом есть совокупность двух лучей, принадлежащих этой прямой.

Может оказаться, что пересечение двух фигур не содержит ни одной точки. В этом случае говорят, что пересечение данных фигур есть пустое множество точек. Так, пересечение прямой с окружностью будет пустым множеством, если расстояние прямой от центра окружности окажется больше радиуса этой окружности. Разность между интервалом прямой и всей прямой есть пустое множество.

Раздел геометрии, в котором изучаются геометрические построения, называют конструктивной геометрией. Основным понятием конструктивной геометрии является понятие построить геометрическую фигуру.

Мы примем это понятие без определения. Конкретный его смысл известен из практики, где оно означает то же, что «начертить», «провести» (линию), «отметить» (точку) и т. п. В интересах логической строгости изложения необходимо чётко формулировать те основные требования (постулаты), которыми характеризуется это понятие. Эти требования обычно не формулируются в условиях школьного курса элементарной геометрии, но они подразумеваются в процессе решения любой геометрической задачи на построение как нечто само собой разумеющееся. Основные требования (постулаты) конструктивной геометрии выражают в абстрактной форме наиболее существенные моменты чертёжной практики. Они являются аксиомами, принимаются без доказательства и служат в дальнейшем логической основой конструктивной геометрии.

Постулаты конструктивной геометрии:

1. Каждая данная фигура построена.

Заметим, что не следует смешивать понятия «данная фигура» и «фигура, заданная (или определённая) такими-то данными её элементами». В последнем случае дана не сама фигура, а лишь некоторые её элементы, которые определяют положение этой фигуры. Например, если даны две точки прямой, то существует единственная прямая, соединяющая эти точки, т. е. эта прямая определена двумя точками, но это не означает, что прямая эта построена (начерчена).

2. Если построены две или более фигуры, то построено и соединение этих фигур.

3. Если построены две фигуры, то можно установить, является ли их разность пустым множеством или нет.

4. Если разность двух построенных фигур не является пустым множеством, то эта разность построена.

Построив две прямые, мы всегда считаем возможным сказать, пересекаются они или нет. Точно так же, если две окружности построены, то мы считаем возможным установить (по чертежу), имеют ли они общие точки. Это же относится к любым двум построенным фигурам.

5. Если две фигуры построены, то можно установить, является ли их пересечение пустым множеством или нет.

Если построены некоторая окружность и точка, то должно быть ясно, лежит ли точка на окружности или нет. Если построены две окружности, то можно сказать, имеют ли они общие точки или нет.

6. Если пересечение двух построенных фигур не пусто, то оно построено.

7. Можно построить любое конечное число общих точек двух построенных фигур, если такие точки существуют.

8. Можно построить точку, заведомо принадлежащую построенной фигуре.

9. Можно построить точку, заведомо не принадлежащую построенной фигуре, если не все точки плоскости принадлежат построенной фигуре.

2.Задача на построение

Задачей на построение называется предложение, указывающее, по каким данным, какими инструментами, какую геометрическую фигуру требуется построить (начертить на плоскости) так, чтобы эта фигура удовлетворяла определённым условиям.

Решить задачу на построение с помощью циркуля и линейки – значит свести её к совокупности пяти элементарных построений, которые заранее считаются выполнимыми. Перечислим их.

1. Если построены две точки А и В, то построена прямая АВ, их соединяющая, а также отрезок АВ и любой из лучей АВ и ВА (аксиома линейки).

2. Если построена точка О и отрезок АВ, то построена окружность с центром в точке О и радиусом АВ, а также любая из дуг этой окружности.

3. Если построены две прямые, то построена точка их пересечения (если она существует).

4. Если построена прямая и окружность, то построена любая из точек их пересечения (если она существует).

5. Если построены две окружности, то построена любая из точек их пересечения (если она существует).

Сведение решения каждой задачи к элементарным построениям делает решение громоздким. Поэтому часто решение задачи сводят к так называемым основным построениям. Выбор некоторых построений в качестве основных в известной степени произволен. Например, в качестве основных построений можно рассмотреть следующие задачи: деление данного угла пополам; построение отрезка, равного данному; построение угла, равного данному; построение параллельной прямой, построение перпендикулярной прямой, деление отрезка в данном отношении; построение треугольника по трём сторонам, по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам; построение прямоугольного треугольника по гипотенузе и катету.

Решить задачу на построение – значит найти все её решения.

Фигуры, удовлетворяющие условию задачи, могут различаться как формой так и размерами, так положением на плоскости. Различия в положении на плоскости принимаются или не принимаются в расчёт в зависимости от формулировки самой задачи на построение, а именно в зависимости от того, предусматривает или не предусматривает условие задачи определённое положение искомой фигуры относительно каких-либо данных фигур.

3.Методы решения задач на построение

Метод параллельного переноса.

Часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и поэтому трудно ввести в чертёж данные. В этих случаях какую-либо часть искомой фигуры переносят или параллельно самой себе, или другим образом, но на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условия задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большее количество данных.

Метод подобия.

Сначала строят фигуру, подобную искомой так, чтобы она удовлетворяла всем условиям задачи, кроме одного. Затем строят уже искомую фигуру, подобную искомой и удовлетворяющую опущенному требованию.

Метод подобия находит применение обычно в случаях, когда среди данных лишь одно является отрезком, а все остальные данные-либо углы, либо отношения отрезков.

Обычно целесообразно вспомогательную фигуру строить так, чтобы она была подобна не только искомой, но и подобно расположена с ней. Успех решения зависит в этих случаях от выбора центра подобия.

При решении задач на построение методом подобия часто воспользоваться следующим замечанием. Если две фигуры подобны, то коэффициент подобия равен отношению любых двух соответствующих отрезков. Если отрезкам a, b, c,… фигуры Ф соответствуют отрезки a₁, b₁, c₁,… подобной фигуры Ф₁, то коэффициент подобия равен также отношениям:

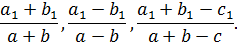
Метод геометрического места точек.

Геометрическим местом точек называется совокупность точек, обладающих некоторыми свойствами. Если задача приводится к определению точки, то можно отбросить одно из условий, которому эта точка должна удовлетворять; тогда искомая точка станет способна принять бесчисленное количество последовательных положений, и все эти положения составят геометрическое место точек, обладающих всеми требуемыми свойствами, кроме отброшенного. Фигура этого геометрического места чаще бывает нам заранее известна; в противном случае её надо определить вспомогательными построениями. Затем, приняв отброшенное условие и откинув какое-либо другое условие задачи, мы вновь увидим, что искомая точка станет способна принять бесчисленное множество новых положений, образующих новое геометрическое место. Определим фигуру этого нового геометрического места, если она нам неизвестна. Тогда искомая точка должна лежать и на первом и на втором геометрическом месте, а потому определяется их пересечением.

Иногда для определения точки достаточно построить одно геометрическое место, потому что другое дано в условии задачи. Если же искомая точка подчинена таким условиям, которые все в совокупности определяют только одно геометрическое место, то задача становится неопределённой.

Алгебраический метод.

Решение задач на построение сводится к построению некоторого отрезка или нескольких отрезков. Величину искомого отрезка выражают через величины известных отрезков с помощью формулы. Затем строят искомый отрезок по полученной формуле.

Метод инверсии.

Пусть нам дана некоторая кривая М и неподвижная точка К – начало или центр инверсии. Возьмём на кривой М точку А и на прямой КА определим точку А₁ так, чтобы абсолютное значение КА·КА₁ = к₂, где к – есть постоянная длина, то при движении точки А по кривой М точка А₁ опишет новую кривую N, которая называется обратной или инвертированной кривой.

Пусть у нас имеется фигура, состоящая из прямых и окружностей. Если эту фигуру инвертировать, то прямые и окружности превратятся в известные прямые и окружности, или в одни окружности, которые будут пересекаться под теми же углами, как и в данной фигуре. Если какая-нибудь точка данной фигуры представляла, например, вершину какого-нибудь угла, то в обратной фигуре она представит, вообще, точку пересечения окружностей, пересекающихся под тем же углом. Словом, обратная фигура удерживает до мельчайших подробностей своеобразное сходство с данной фигурой.

Зная отображённую фигуру и положение начала инверсии, нередко можно легко отгадать форму основной фигуры; что касается её размера, то для этого нужно знать степень инверсии.

4.Задачи на построение в системе задач школьного курса геометрии

1) Виленкин Н.Я., «Математика», 5 класс.

В этом учебнике в главе 1, впервые построение с помощью линейки появляется в §1. Здесь от учащихся требуется построить сначала отрезок, а затем многоугольник. В главе 2, в пункте «Окружность и круг» автор дает задание на построение окружности с помощью циркуля. И в завершение курса, учащиеся учатся строить прямые углы.

Виленкин Н.Я., «Математика», 6 класс.

В самом конце учебника даются задания на построение перпендикулярных и параллельных прямые с помощью чертежного треугольника и линейки.

2) Дорофеев Г.В. «Математика», 5 класс.

В этом учебнике школьники учатся строить прямую, проходящую через две данные точки, а также окружности с помощью циркуля. И, в завершение, даются задачи на построение углов, в том числе и с помощью угольника.

Дорофеев Г.В. «Математика», 6 класс.

В этом учебнике школьники сначала строят перпендикулярные и параллельные прямые с помощью чертежного треугольника и линейки. Далее они решают различные задачи на построение

· касательной к окружности;

· окружности, касающейся двух параллельных прямых;

· двух окружностей.

После изучения понятия «симметрия» школьники решают задачи на построение симметричных фигур. После изучения фигур на плоскости шестиклассники рассматривают построение треугольников по трем сторонам и решают задачи на построение различных треугольников (прямоугольных, равнобедренных, остроугольных, тупоугольных).