Связанные определения

Изоморфизм алгебраической системы на себя называется автоморфизмом.

История

Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.

Вариации и обобщения

· Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).

Евклидова геометрия

Евкли́дова геоме́трия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.).

Основные сведения

Элементарная геометрия — геометрия, определяемая в основном группой перемещений (изометрий) и группой подобия. Однако содержание элементарной геометрии не исчерпывается указанными преобразованиями. Так, к элементарной геометрии также относят преобразование инверсии, вопросы сферической геометрии, элементыгеометрических построений, теорию измерения геометрических величин и другие вопросы.

Элементарную геометрию часто называют евклидовой геометрией, так как первоначальное и систематическое её изложение, хотя и недостаточно строгое, было в «Началах» Евклида. Первая строгая аксиоматика элементарной геометрии была дана Гильбертом. Элементарная геометрия изучается в средней общеобразовательной школе.

Аксиоматика

Проблема полной аксиоматизации элементарной геометрии — одна из проблем геометрии, возникшая в Древней Греции в связи с критикой этой первой попытки построить полную систему аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.

В «Началах» Евклида была дана следующая аксиоматика:

1. От всякой точки до всякой точки можно провести прямую.

2. Ограниченную прямую можно непрерывно продолжать по прямой.

3. Из всякого центра всяким раствором может быть описан круг.

4. Все прямые углы равны между собой.

5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Исследование системы аксиом Евклида во второй половине XIX века показало её неполноту.

В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до ГильбертаПашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.

Существуют и другие современные аксиоматики, наиболее известные:

· аксиоматика Тарского

· аксиоматика Биргофа, содержащая всего 4 аксиомы, но использующая вещественные числа как готовое понятие.

ОСНОВАНИЯ ГЕОМЕТРИИ

раздел геометрии, в котором исследуются основные понятиягеометрии, соотношения между ними и связанные с ними вопросы.

Важная роль основных понятий и соотношений между ними, на базе к-рых строятся определения фигур идоказываются геометрич. предложения, отмечается уже в работах античных геометров. Так, развиваядедуктивный метод в геометрии, они указывали на особую роль основных понятий, аксиом и постулатов,составляющих фундамент геометрии. В "Началах" Евклида (3 в. до н. э.) аксиомам и постулатампредпослана цепь определений всех понятий, которые используются в дальнейшем изложении. Среди этихопределений особое место принадлежит понятиям "точка", "прямая", "плоскость", определения к-рых неопираются на другие геометрич. понятия. Сами определения этих основных понятий с геометрич. точкизрения неудовлетворительны, т. к. они выражают лишь характерное физич. свойство (напр., "точка есть то,что не имеет частей", т. е. под точкой понимается малое физически неделимое тело). Поэтому уже в трудахгеометров, написанных почти одновременно с "Началами", содержатся многочисленные комментарии икритич. анализ определений основных и других геометрич. понятий, аксиом и постулатов. Но это были лишьуточнения, не затрагивающие основы определений. По существу, доказательства многих гоометрич. теоремопирались в основном на наглядность чертежа, на физич. осуществимость необходимых геометрич.построений, а не выводились строго логически из аксиом и постулатов. Только в 19 в. и особенно в нач. 20 в.появляются работы, в к-рых выясняется все глубокое значение основных понятий и соотношений междуними для логически безупречного дедуктивного метода построения геометрии и ее обоснования. Причем вомногом этому углубленному анализу основ геометрии способствовало открытие неевклидовой геометрииЛобачевского (1826). Результаты по обоснованию евклидовой геометрии на основе тех же принципов ипонятий, что и в "Началах" Евклида, содержатся в работах Дж. Пеано (G. Реапо, 1894), М. Паша (М. Pasch,1882), М. Пиери (М. Pieri, 1899), Д. Гильберта (D. Hilbert) и др. Наибольшую известность получила Гильбертасистема аксиом евклидовой геометрии (1899). Добиваясь логически удовлетворительного построенияевклидовой геометрии, Д. Гильберт выделил 5 групп аксиом, показал их необходимость и достаточность дляпостроения всей евклидовой геометрии. Вместе с тем впервые была проведена логич. обработка всейсистемы, выяснена непротиворечивость системы с помощью построения числовой модели, установленанезависимость групп аксиом, а также полнота системы. В отличие от концепции пространства как "места"для всех фигур, проводимой в "Началах", Д. Гильберт рассматривает его как множество всех "точек", "прямых", "плоскостей" и фигур, построенных на основе этих понятий.

Набор основных понятий в системе Гильберта был заимствован (и уточнен) из "Начал", однако эта системаявляется, по существу, чисто геометрич. схемой, свободной от ссылок на наглядность чертежа. Вместе стем язык геометрии, построенной на основе системы Гильберта, почти не отличается от языка "Начал".

Почти одновременно с системой Гильберта появились и др. системы аксиом евклидовой геометрии. Так, всистеме Ф. Шура (F. Schur, 1909) в качестве основных понятий были "точка", "отрезок" и т. д., а вместо"конгруэнтности" фигур в этой системе вводилось понятие "движение". Введение понятия "движение"позволило применить в геометрии групповой подход к исследованию движений, алгебраизировать методыисследования. Упомянутые выше геометрич. схемы не полностью удовлетворяют требованиямдальнейшего обобщения понятия пространства и др. понятий и, кроме того, недостаточно "алгебраичны".

Новые подходы к обоснованию евклидовой геометрии потребовали выработки нового "языка", с помощью к-рого оказывается возможным провести соответствующие дальнейшие обобщения понятий, алгебраизациюдоказательств, классификацию объектов и т. д. Одной из распространенных схем основания евклидовойгеометрии, в к-рой сконцентрированы возможности обобщений, перевода на язык алгебры геометрич.понятий, является система аксиом, предложенная Г. Вейлем (Н. Weil, 1916). Ниже приводится одна изтранскрипций схемы Вейля.

Трехмерное евклидово пространство 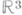определяется как множество, состоящее из элементов двух родов - "точек" и "векторов", удовлетворяющих следующим 4 группам аксиом:

I группа - аксиомы, определяющие соотношения между точками и векторами. I _Х. Существует по меньшеймере одна точка. I₂. Каждой упорядоченной паре точек поставлен в соответствие один и только один вектор.I₃- Для каждой точки Аи каждого вектора асуществует одна и только одна точка Втакая, что

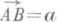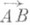( есть вектор я). I₄. Если 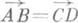, то = .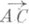

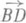На основе этой группы аксиом определяется сумма векторов, к-рая удовлетворяет требованиямкоммутативности и ассоциативности. Существует нуль-вектор, противоположный вектор. Векторы посложению образуют группу.

II группа - аксиомы, описывающие операцию умножения вектора на число. II₁. Каждому вектору а и каждому 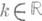поставлен в соответствие определенный вектор k a (k a наз. произведением вектора а, на число k). II₂.Умножение вектора на 1. не изменяет вектора. II₃. Умножение вектора на число дистрибутивноотносительно сложения чисел (k₁+k₂) a = k₁ a +k₂ a. II₄. Умножение вектора на число дистрибутивноотносительно сложения векторов k(a ₁+ a ₂)= k a ₁+k a ₂ II₅. Умножение вектора на число ассоциативно

k₁ (k₂ a)=(k₁k₂) a

С помощью операций сложения и умножения на число определяется линейная комбинация векторов, ихлинейная зависимость.

III группа определяет размерность пространства. III_i. Существуют три линейно независимых вектора, новсякие четыре - линейно зависимы.

Эта аксиома имеет топологич. характер; из нее вместе со второй группой аксиом следует, что R³ являетсятопологич. пространством размерности 3. Первые три группы аксиом определяют трехмерное аффинноепространство.

IV группа определяет метрич. свойства. IV₁. Любым двум векторам а и b поставлено в соответствиеопределенное число (скалярное произведение) (a, b) =l, . IV₂. Симметричность скалярногопроизведения: (a, b) = (b, a). IV₃. Дистрибутивность скалярного произведения (а, b+c)=(a, b)+(а, с). IV₄. Для 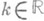имеет место (a, k b) =k (a, b). IV₅. Скалярный квадрат вектора неотрицателен 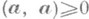, причем (а,a)=0 только для нуль-вектора.

На основе IV группы аксиом определяется расстояние между точками, угол между векторами и т. д.; спомощью векторов - "отрезки", "прямые", "плоскости" и т. д.