Тавтологическое расслоение

Тавтологическим расслоением называется векторное расслоение, пространством расслоения которого является подмножество прямого произведения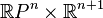

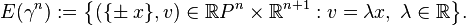
а слоем — вещественная прямая 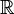. Каноническая проекция 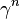отображает прямую, проходящую через точки 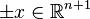, в соответствующую точку проективного пространства. При 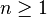это расслоение не является тривиальным. При 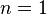пространством расслоения является лента Мёбиуса.

Понятие о математической структуре

Структура, решётка (математическая); важное алгебраическое понятие. С. называется непустое множество S, для элементов которого определены две операции — объединение и пересечение, обозначаемые соответственно значками È и Ç (т. е. каждой паре элементов а и b из S однозначно сопоставлен элемент a È b из S — их объединение и элемент а Ç b из S — их пересечение), причём эти операции удовлетворяют следующим условиям (аксиомам С.):

1. Ассоциативность == (a È b) È с, = a È(b Èс):

(a Ç b) Ç с= а Ç (b Ç с);

II. Коммутативность a È b = b È а;

a Ç b) =b Ç а,

III. Абсорбция (а È b) Ç а= а.

(a Ç b) È а== а.

Примеры С.: 1) множество целых положительных чисел с операциями взятия наибольшего общего делителя и наименьшего общего кратного; 2) множество всех подмножеств произвольного множества с операциями взятия теоретико-множественных объединения и пересечения подмножеств; 3) множество действительных чисел с операциями взятия большего и меньшего числа из двух данных чисел.

Подробно изучены различные специальные типы С., т. е. С., на которые наложены дополнительные условия (например, дистрибутивные С., модулярные, или дедекиндовы, С., С. с дополнениями). Весьма важным частным случаем С. являются булевы алгебры, т. е. дистрибутивные С. с единицей и нулём, обладающие дополнениями к каждому элементу. Булевы алгебры имеют большое значение для математической логики и теории вероятностей. Другие типы С. находят применение в теории множеств, топологии, функциональном анализе.

Изоморфизм

Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое употребляется в различных разделахматематики. В общих чертах его можно описать так: пусть даны две алгебраические структуры (группы, кольца, линейные пространства и т. п.). Обратимое отображение (биекция) между ними называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.

Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными» и называются изоморфными. Классическим примером изоморфных систем могут служить множество 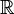всех вещественных чисел с определённой на нём операцией сложения и множество положительных вещественных чисел с заданной на нём операцией умножения. Отображение в этом случае является изоморфизмом.

Общая алгебра

В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.

Группы

Пусть 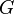и — две группы. Биекция называется изоморфизмом, если для любых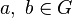

.

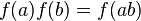Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.^[1]

Поля

Пусть 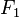и 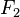— поля. Биекция называется изоморфизмом, если для любых 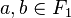выполняется

1. ,

2. .

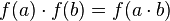Теория множеств

В теории множеств любая биекция является изоморфизмом.