Постановка задачи. Выпуклой задачей (или задачей выпуклого программирования) называется следующая задача оптимизации:

Выпуклой задачей (или задачей выпуклого программирования) называется следующая задача оптимизации:

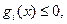
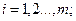
(36.1)

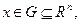
где 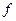, , 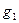,...., 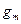– выпуклые функции, заданные на выпуклом и замкнутом множестве G.

Точка х, принадлежащая множеству G и удовлетворяющая неравенствам 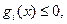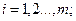. называется допустимой в задаче (36.1).

Если функция f определена и выпукла на выпуклом множестве 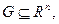то в выпуклой задаче локальный минимум является и глобальным.

Пусть х – точка локального минимума функции 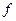, т.е. 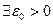такое, что

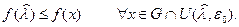
Возьмем произвольную фиксированную точку 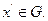Из условия выпуклости множества G следует, что точка

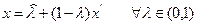
принадлежит множеству G.

При

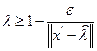
где

получаем

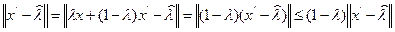
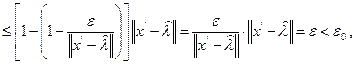
что означает

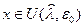
и, следовательно,

По условию функция 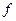выпукла. Поэтому последнее неравенство примет вид

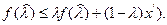
В частности, при

имеем

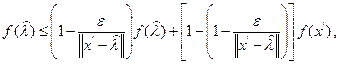
Отсюда

или

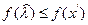
Так как – произвольная точка множества , то из последнего неравенства следует, что – точка глобального минимума функции 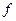на .

В дальнейшем в выпуклых задачах оптимизации, говоря "минимум", будем, подразумевать глобальный минимум.

Условия оптимальности в выпуклых задачах

В выпуклых задачах оптимизации важное место занимает функция Лагранжа и понятие так называемой седловой точки функции Лагранжа.

Пусть – декартово произведение множества (области определения функций и 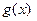, 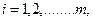в задаче (36.1))и множества 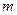-мерных векторов с неотрицательными координатами

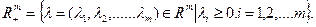
Функция

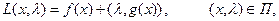(36.2)

где

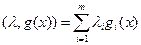
– скалярное произведение векторов и 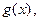, называется функцией Лагранжа для выпуклой задачи оптимизации (36.1).

Точка называется седловой точкой функции Лагранжа 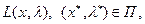если выполняются неравенства

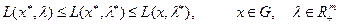(36.3)

Условие (36.3) может быть записано также следующим образом

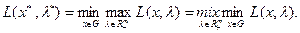
В задачах с ограничениями типа равенств, как это отмечалось выше, решение следовало искать среди стационарных точек функции 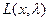. Что же касается выпуклой задачи оптимизации, то ее решение сводится к отысканию седловой точки функции Лагранжа.

Если пара 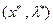– седловая точка функции Лагранжа (36.2), то 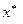– точка глобального минимума в задаче (36.1), т.е.

Пусть 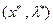– некоторая седловая точка функции Лагранжа. Из (36.2) и (36.3) получаем

(36.4)

Из левой части неравенства (36.4) следует, что

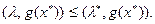(36.5)

Отсюда

или в развернутом виде

(36.6)

Поскольку 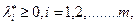неравенство (36.6) имеет место, если

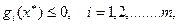
Итак, и, кроме того, 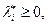поэтому

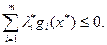(36.7)

Равенство (36.6) справедливо, в частности, и для 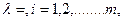т.е.

(36.8)

Сравнивая неравенства (36.7) и (36.8), будем иметь

т.е.

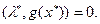(36.9)

Так как

то

или

(36.10)

Неравенство (36.4) имеет место 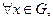, поэтому из его правой части и из (36.9)-(36.10) получим

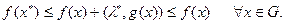
Следовательно, 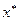– точка глобального минимума.

Для того чтобы пара 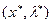являлась седловой точкой функции Лагранжа (36.2), необходимо и достаточно выполнение условий

(36.11)

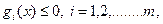(36.12)

(36.13)

Необходимость. Пусть 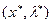– седловая точка функции (36.2). Тогда по определению

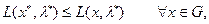
что означает справедливость равенства (36.11).

Выполнение условий (36.12) и (36.13) было показано при доказательстве теоремы (36.2).

Достаточность. Пусть выполнены условия (36.11)-(36.13). Равенство (36.11) влечет справедливость правой части неравенства (36.3) . Докажем выполнение левой части неравенства (36.3) для всех . Для этого рассмотрим произвольные неотрицательные числа .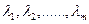

Очевидно,

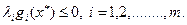
Поэтому, используя неравенства (36.12) и (36.13), можно записать:

Следовательно,

что означает справедливость левой части неравенства (36.3).

Условия, при выполнении которых хотя бы одна седловая точка функции Лагранжа всегда существует, сформулированы в следующем утверждении.

Пусть функции 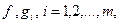выпуклы на выпуклом множестве 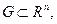имеет место условие (условие Слейтера):

что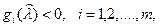

и 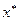– точка глобального минимума в задаче (36.1). Тогда найдется такой вектор что пара 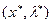– седловая точка функции Лагранжа (36.2).

Отсюда вытекает следующие необходимое условие оптимальности: для того чтобы х* была точкой глобального минимума в выпуклой задаче оптимизации (36.1), необходимо, чтобы нашелся такой вектор , что пара 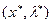образует седловую точку функции Лагранжа.

Таким образом, исходную задачу (36.1) можно заменить задачей отыскания седловой точки функции Лагранжа.