Метод золотого сечения

Метод "золотого" сечения требует только унимодальности функции .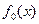

"Золотое" сечение, открытое Евклидом, состоит в разбиении интервала [ а, b ] точкой x ₁ на две части таким образом, чтобы отношение большей части к длине всего интервала было равно отношению меньшей части к большей.

. (33.1)

Представим интервал [ а, b ] как совокупность двух отрезков:

. (7.2)

Разделив уравнение (33.2) на (b - а), получим:

.

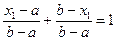Так как 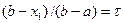и 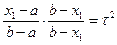, имеем 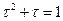, корни которого определяются по формуле:

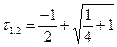т.е. .

Из уравнения (33.1) следует

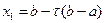. (33.3)

Проведем "золотое" сечение относительно точки а, получим

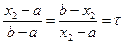. (33.4)

Из уравнения (33.4) получим формулу для определения точки x ₂:

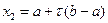. (33.5)

Заметим, что точка x ₁ производит "золотое" сечение интервала [ а, x ₂], а точка x ₂ – интервала [ x ₁, b ].

Для унимодальной функции, зная значения функции в точках золотого сечения 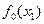и 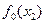, можно определить интервал неопределенности, в котором находится 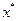. После выбора на оставшемся интервале нужно определить только одну точку, производящую "золотое" сечение. Для выбранного интервала [ а, x ₂] следует положить b = x ₂, x ₂= x ₁ и пересчитать точку x ₁ по формуле (33.3), а для [ x ₁, b ] – a = x ₁, x ₁= x ₂ и пересчитать точку x ₂ по формуле (33.5). На каждом шаге итерации длина интервала неопределенности уменьшается и составляет примерно 0,62 длины предыдущего интервала неопределенности. Итерационную процедуру следует закончить, когда длина интервала неопределенности станет меньше или равна заданной точности.

Алгоритм метода "золотого" сечения:

1. Ввод a, b, ε. Вычисляем значения x ₁ и x ₂ по формулам (33.3), (33.5).

2. Вычисляем 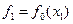и .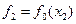

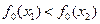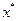3. Если , то находится в интервале [ а, x ₂] (рис.33.1б), т.е. b = x ₂. Переопределяем точки x ₂= x ₁ и f ₂= f ₁, пересчитываем точку x ₁ по формуле (33.3) и вычисляем f ₁. Переходим на п.4.

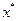Если , то находится в интервале [ x ₁, b ] (рис.33.1а), т.е. a = x ₁, x ₁= x ₂, f ₁= f ₂. Пересчитываем точку x ₂ по формуле (33.5) и вычисляем f ₂.

4. Проверка (b – а)< ε, если нет, то переходим на п.3, да – на п.5.

5. Печать 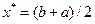, оптимального значения критерия 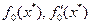, для контроля правильности полученных данных.

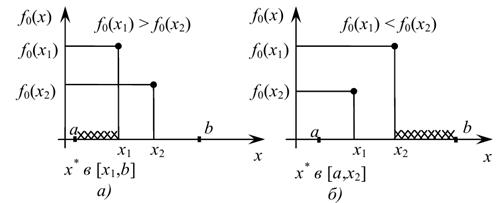
Рис.33.1

Лекция №34