 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
График эмпирической функции распределения
|
|
5) Мода 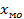 - значение признака с наибольшей частотой;
- значение признака с наибольшей частотой;
Медиана 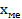 значение признака, расположенного в середине ряда распределения. Мода и медиана являются структурными (распределительными) средними.
значение признака, расположенного в середине ряда распределения. Мода и медиана являются структурными (распределительными) средними.
Для определения моды сначала находят интервал с наибольшей частотой 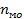 = 8. В этом интервале число правильных ответов 32-36. Точное значение моды
= 8. В этом интервале число правильных ответов 32-36. Точное значение моды 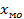 находят путем интерполяции по формуле
находят путем интерполяции по формуле
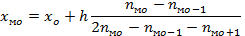
Где h - шаг интервала, 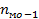 - частота предмодального интервала,
- частота предмодального интервала, 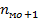 - частота постмодального интервала.
- частота постмодального интервала.
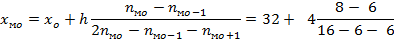
=  4=34
4=34
Значение медианы 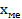 также определяем путем интерполяции по формуле
также определяем путем интерполяции по формуле
 .
.
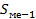 - накопленные частоты интервалов, предшествующих меданному.
- накопленные частоты интервалов, предшествующих меданному.
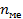 - локальная частота интервала, в котором находятся единицы совокупности, делящие ряд пополам,
- локальная частота интервала, в котором находятся единицы совокупности, делящие ряд пополам, 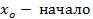 медианного интервала.
медианного интервала.
 , следовательно медианным является интервал с накопленной частотой 20, его частота составляет
, следовательно медианным является интервал с накопленной частотой 20, его частота составляет 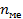 =10,
=10, 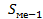 =14.
=14.
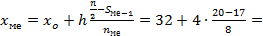
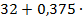 4=33,5
4=33,5
| xi | |||||||||
| ni |
Найдем методом произведений выборочные: среднюю, дисперсию, среднее квадратическое отклонение, начальные и центральные моменты до четвертого порядка включительно.
Составляем таблицу:
Таблица 1.
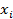
| 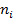
| 
| 
| 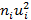
| 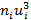
| 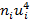
| 
| ||
| -4 | -4 | -64 | |||||||
| -3 | -12 | -108 | |||||||
| -2 | -12 | -48 | |||||||
| -1 | -6 | -6 | |||||||
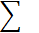
| n=40 |  = -2 = -2
| 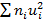 =170 =170
| 
| 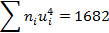
| 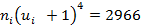
| |||
В качестве ложного нуля принимаем С= 34– варианта с наибольшей частотой 10 и находящаяся в середине вариационного ряда. Шаг выборки h=4. Тогда условные варианты определяются по формуле
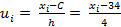 .
.
Подсчитываем все варианты  и заполняем все столбцы.
и заполняем все столбцы.
Последний столбец служит для контроля вычислений по тождеству:
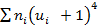 =
= 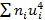 + 4
+ 4 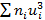 + 6
+ 6 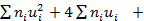 n=
n= 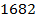 +4
+4 
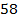 +6
+6  170 +4
170 +4 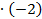 +40=
+40= 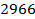 .
.
Вычисления произведены верно. Найдем условные начальные моменты.
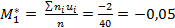 .
. 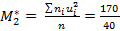 = 4, 25.
= 4, 25.
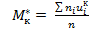 - условные начальные моменты к- го порядка
- условные начальные моменты к- го порядка
Вычисляем выборочную среднюю:
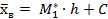 =
= 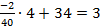 3,8.
3,8.
Находим выборочную дисперсию:
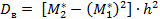 =
= 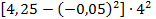 = 4,2475
= 4,2475  = 67,96.
= 67,96.
Определяем выборочное среднее квадратическое отклонение:
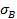 =
= 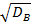 =
= 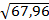 =8,2437.
=8,2437.
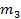 =
= 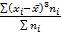 .
. 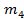 =
= 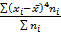 центральные эмпирические моменты третьего и четвертого порядков.
центральные эмпирические моменты третьего и четвертого порядков.
Эти моменты в случае равноотстоящих вариант с шагом 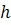 вычисляются по формулам:
вычисляются по формулам:
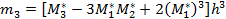

Ассиметрия и эксцесс определяются равенствами: 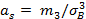 ,
, 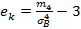
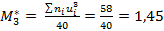 ,
,
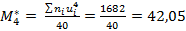 ,
,
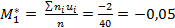 .
. 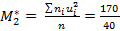 = 4, 25.
= 4, 25.
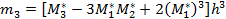 =
= 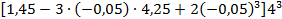 =2,08725
=2,08725 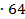 = 133,584
= 133,584
 =
=  =42,4
=42,4 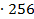 = 10855,3552
= 10855,3552
Коэффициент вариации находим по формуле:
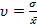 · 100%.
· 100%.  · 100% =24, 39 %.
· 100% =24, 39 %.
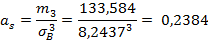
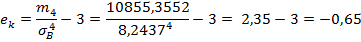
6. Строим нормальную кривую.
Для облегчения вычислений все расчеты сводим в таблицу 2
Таблица 2.
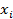
| 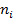
| 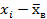 = = 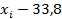
| 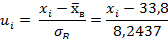
| 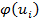
| 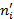 = 19, 4 = 19, 4 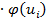
|
| -15,8 | -1,91654 | 0,0644 | 1,24936 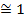
| ||
| -11,8 | -1,43134 | 0,1435 | 2,7839 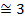
| ||
| -7,8 | -0,94614 | 0,2565 | 4,9761 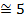
| ||
| -3,8 | -0,46094 | 0,3589 | 6,96266 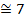
| ||
| 0,2 | 0,02426 | 0,3989 | 7,73866 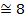
| ||
| 4,2 | 0,50946 | 0,3521 | 6,83074 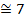
| ||
| 8,2 | 0,99466 | 0,2444 | 4,74136 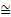 5 5
| ||
| 12,2 | 1,47986 | 0,1334 | 2,58796 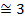
| ||
| 16,2 | 1,96506 | 0,058 | 1,1252 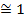
| ||
| n=40 | n=40 |
Заполняем первые три столбца.
В четвертом столбце записываем условные варианты по формуле, указанной в «шапке» таблицы. В пятом столбце находим значения функции
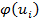 =
= 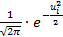 .
.
Функция 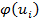 четная,т.е.
четная,т.е.  .Значения функции
.Значения функции 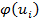 в зависимости от аргумента
в зависимости от аргумента  (берутся положительные
(берутся положительные  , т.к.
, т.к. 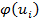 четная) находим из таблицы.
четная) находим из таблицы.
Теоретические частоты теоретической кривой находим по формуле
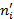 =n
=n 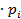 ,
,
где 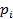 - вероятность попадания Х в i-частичный интервал с концами
- вероятность попадания Х в i-частичный интервал с концами
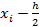 и
и 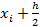 .
.
Приближенно вероятности могут быть найдены по формуле 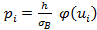 .
.
Тогда теоретические частоты равны равны
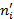 =n
=n 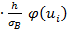 =
= 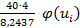 = 19, 4
= 19, 4 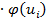 .
.
Заполняем последний столбец. В последнем столбце частоты 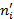 округляются до целого числа и
округляются до целого числа и 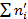 =
= 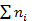 =40.
=40.
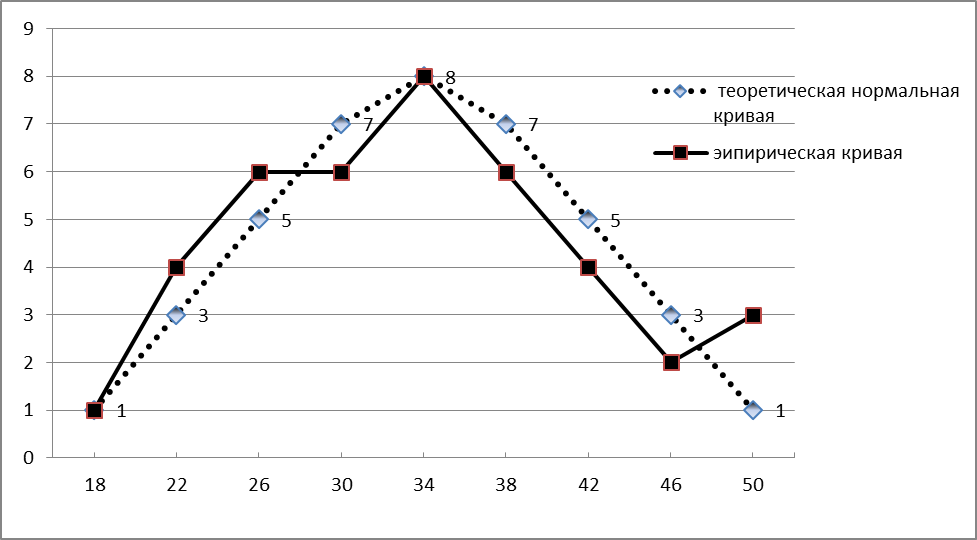
В системе координат (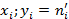 ) строим нормальную (теоретическую кривую)кривую по выравнивающим частотам
) строим нормальную (теоретическую кривую)кривую по выравнивающим частотам 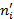 и полигон наблюдаемых частот
и полигон наблюдаемых частот 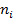 . Полигон наблюдаемых частот построен в системе координат (
. Полигон наблюдаемых частот построен в системе координат (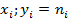 ).
).
7. Проверяем гипотезу о нормальности Х при уровне значимости  =0,05.
=0,05.
В качестве статистики 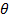 выбирают СВ
выбирают СВ 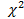 :
:
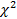 =
= 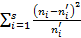 .
.
Она подчиняется распределению 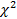 с числом степеней свободы
с числом степеней свободы 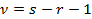 , где s - число различных значений
, где s - число различных значений 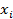 ;
;  - число параметров, откоторых зависит распределение. Для нормального закона таких параметров два: a=
- число параметров, откоторых зависит распределение. Для нормального закона таких параметров два: a= 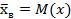 и
и 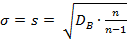 , т.е.
, т.е. 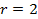 , и
, и  . По данному уровню значимости
. По данному уровню значимости  и числу степеней свободы
и числу степеней свободы 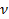 в таблице распределения
в таблице распределения 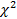 находят критическое значение
находят критическое значение 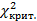 и находят критическую область:
и находят критическую область: 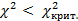 ,
, 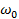 =
=  . Затем вычисляем наблюдаемое значение
. Затем вычисляем наблюдаемое значение 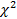 , т.е.
, т.е.  по формуле
по формуле
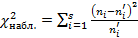 .
.
Если окажется, что 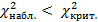 , то нулевую гипотезу
, то нулевую гипотезу 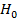 о том,что Х имеет нормальное распределение, принимают. В этом случае опытные данные хорошо согласуются с гипотезой о нормальном распределении генеральной совокупности.
о том,что Х имеет нормальное распределение, принимают. В этом случае опытные данные хорошо согласуются с гипотезой о нормальном распределении генеральной совокупности.
Вычислим  , для чего составим расчетную таблицу 3.
, для чего составим расчетную таблицу 3.
Таблица 3
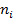
| 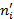
| 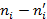
| 
| 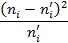
| 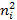
| 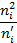
|
| 0,333333 | 5,333333 | |||||
| 0,2 | 7,2 | |||||
| -1 | 0,142857 | 5,142857 | ||||
| -1 | 0,142857 | 5,142857 | ||||
| -1 | 0,2 | 3,2 | ||||
| -1 | 0,333333 | 1,333333 | ||||
| n=40 |  =
5,352381 =
5,352381
| 45,35238 |
Суммируя числа пятого столбца, получаем  = 5,352381
= 5,352381
Суммируя числа последнего столбца, получаем 45,35238
Контроль:  =5,352381
=5,352381
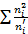 -
-  = 45,35238-40=5,352381
= 45,35238-40=5,352381
Совпадение результатов подтверждает правильность вычислений.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариантов) 7, 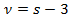 =9-3=6.
=9-3=6.
По таблице критических точек распределения 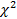 , по уровню значимости
, по уровню значимости  и числу степеней свободы
и числу степеней свободы  6 находим
6 находим 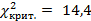 .
.
Так как 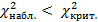 ,то нет оснований отвергнуть нулевую гипотезу. Расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
,то нет оснований отвергнуть нулевую гипотезу. Расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
8. Найдем доверительный интервал для оценки неизвестного математического ожидания, полагая, что Х имеет нормальное распределение, среднее квадратическое отклонение 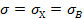 = 8,2437и доверительную вероятность
= 8,2437и доверительную вероятность 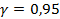 .
.
Известен объем выборки: n=40, выборочная средняя 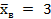 3,8.
3,8.
Из соотношения 2 
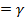 получим
получим 
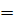 0,475. По таблице находим параметр t=1,96.
0,475. По таблице находим параметр t=1,96.
Найдем точность оценки
 = 2,55
= 2,55
Доверительный интервал таков:
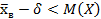 <
< 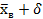 или
или 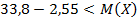 <
< 
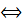 или
или 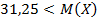 <
< 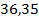 .
.
Надежность 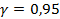 указывает, что если произведено достаточно большое число выборок, то 95 % из них определяет такие доверительные интервалы, в которых параметр действительно заключен.
указывает, что если произведено достаточно большое число выборок, то 95 % из них определяет такие доверительные интервалы, в которых параметр действительно заключен.
Интервальная оценка для среднего квадратического отклонения:
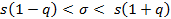 .
. 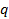 находим по таблице по заданным n и
находим по таблице по заданным n и 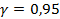 .
.
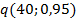 = 0,24
= 0,24

Тема 2
Статистическое исследование зависимостей (корреляционно- регрессионный анализ)
Рассмотрим выборку двумерной случайной величины (Х, Y). Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним 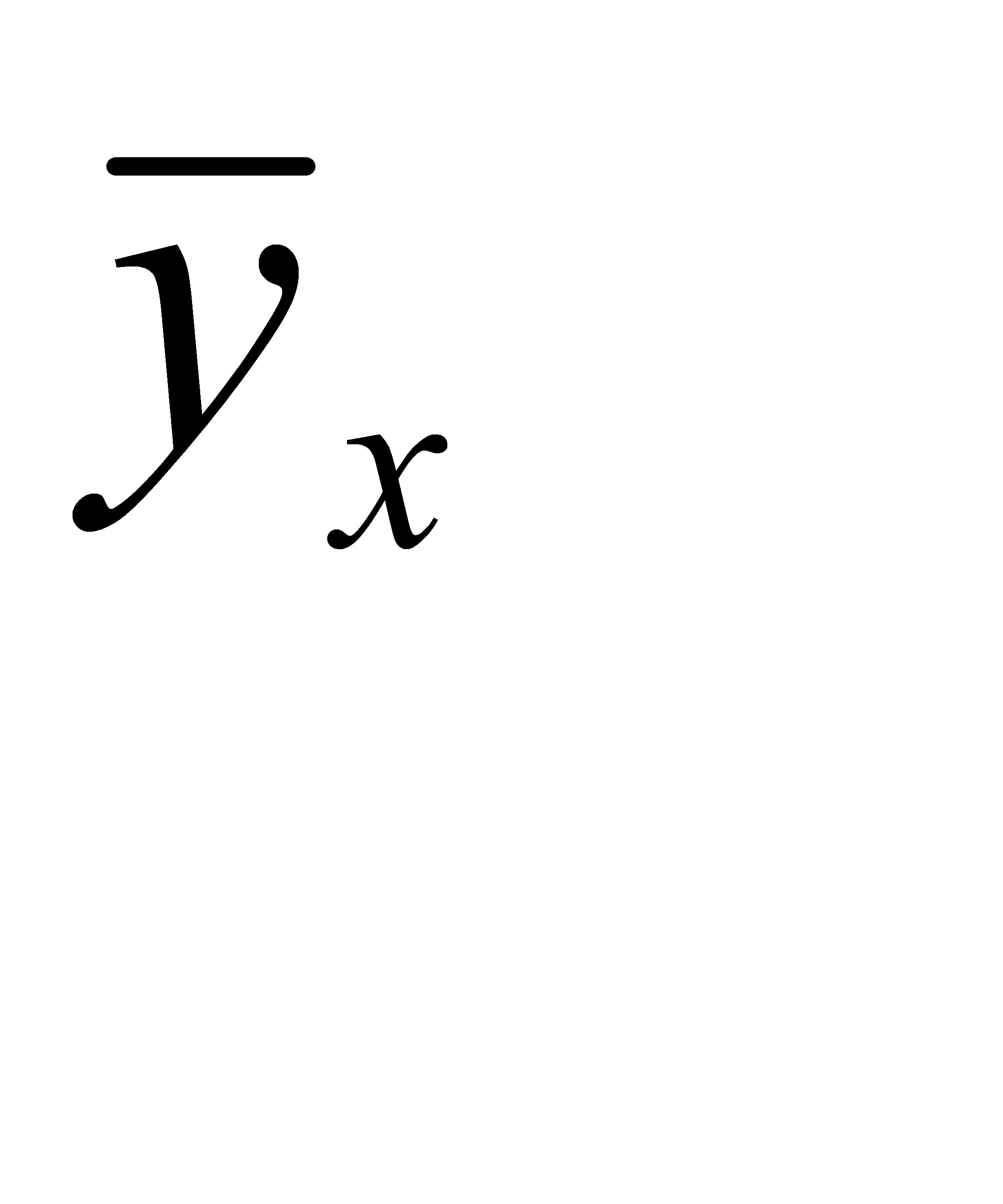 назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее
назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее 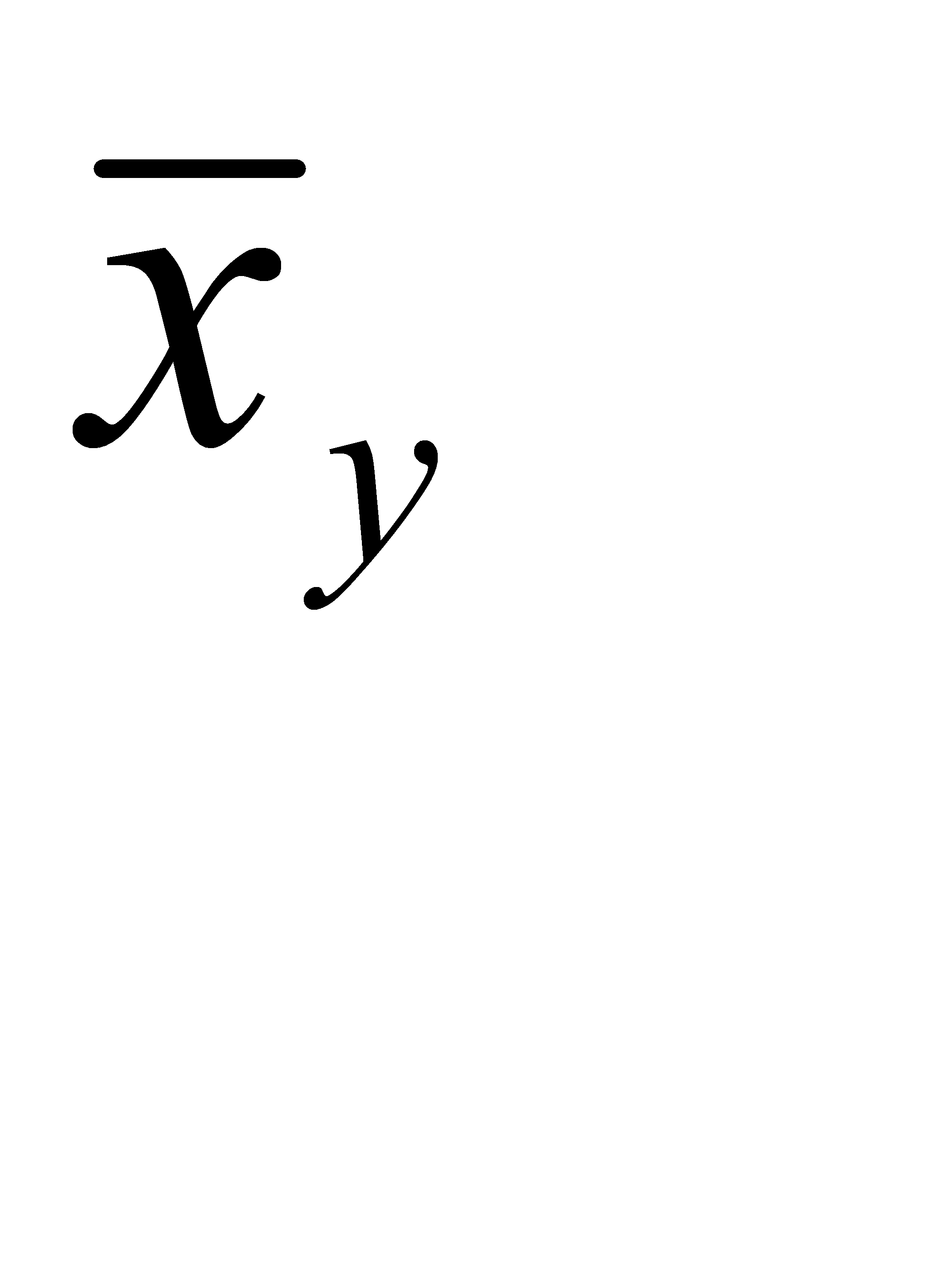 - среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. Уравнения регрессии Y на Х и Х на Y
- среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. Уравнения регрессии Y на Х и Х на Y
имеют вид:
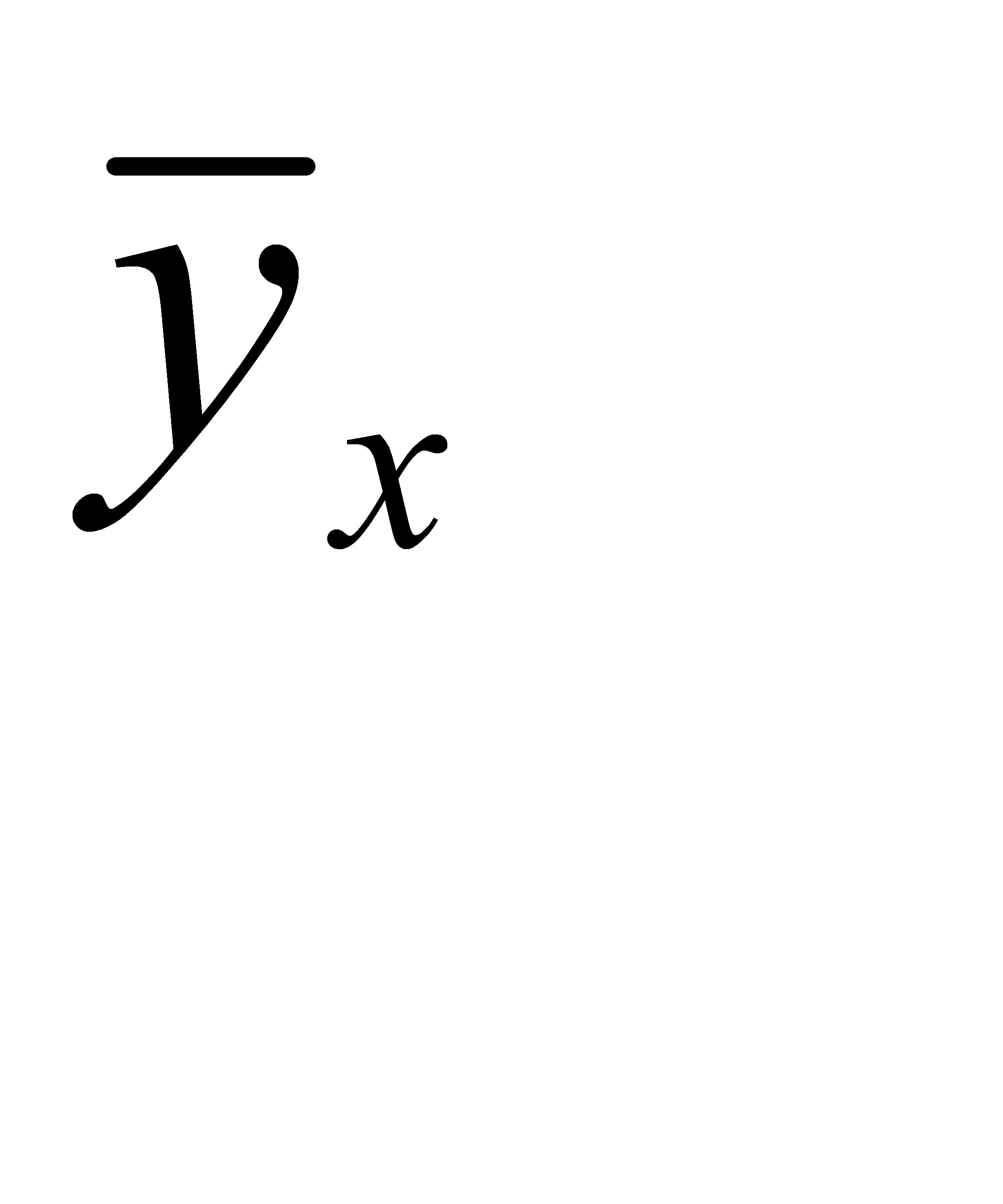 = f* (x) -
= f* (x) -
- выборочное уравнение регрессии Y на Х,
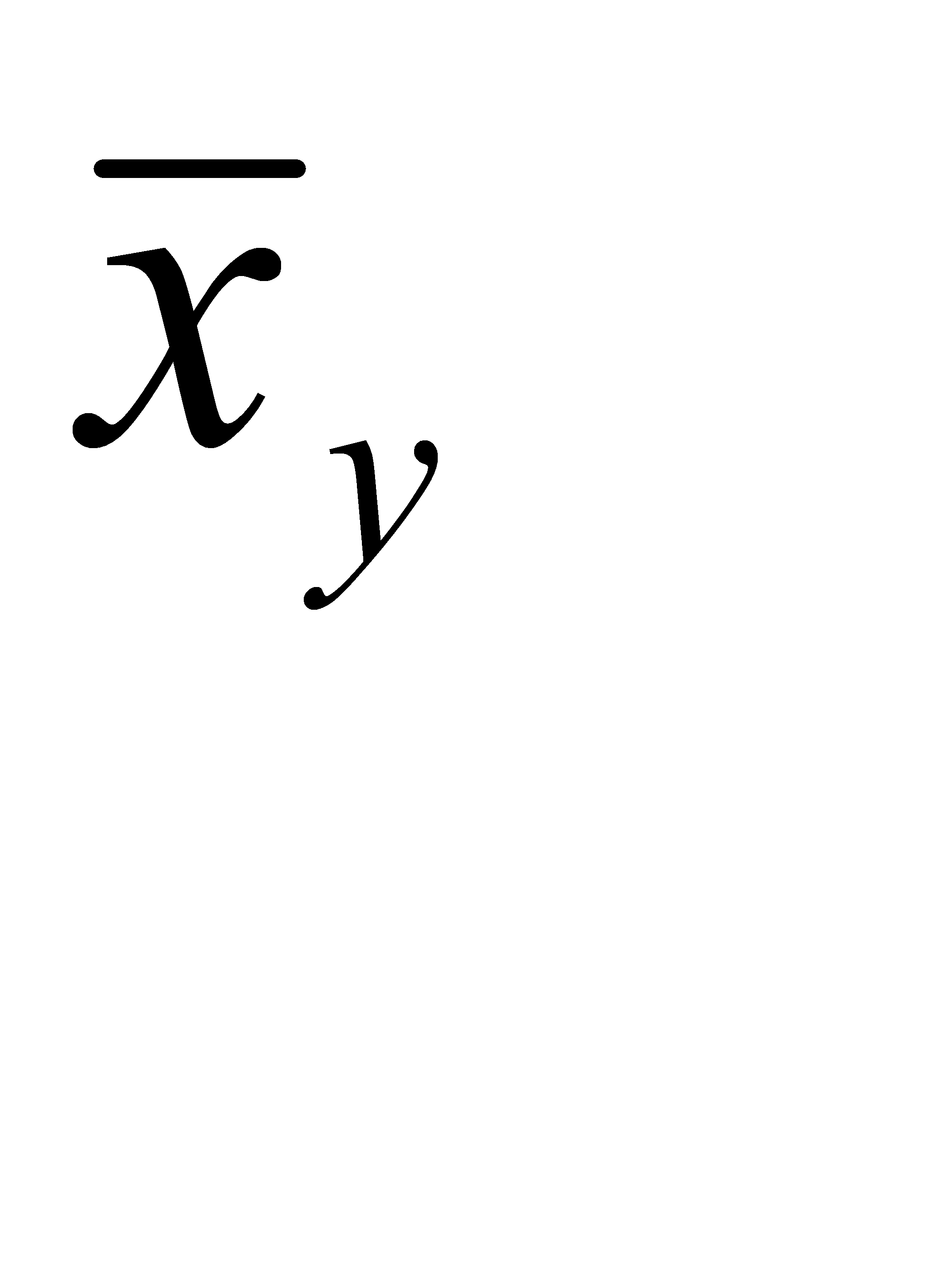 = φ * (у) -
= φ * (у) -
- выборочное уравнение регрессии Х на Y.
Соответственно функции f* (x) и φ* (у) называются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если сам вид этих уравнений известен.
Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х 1, у 1), (х 2, у 2),…, (хп, уп). Будем искать параметры прямой линии регрессии Y на Х вида
Y = ρyxx + b,
подбирая параметры ρух и b так, чтобы точки на плоскости с координатами (х 1, у 1), (х 2, у 2), …, (хп, уп) лежали как можно ближе к прямой. Используем для этого метод наименьших квадратов и найдем минимум функции
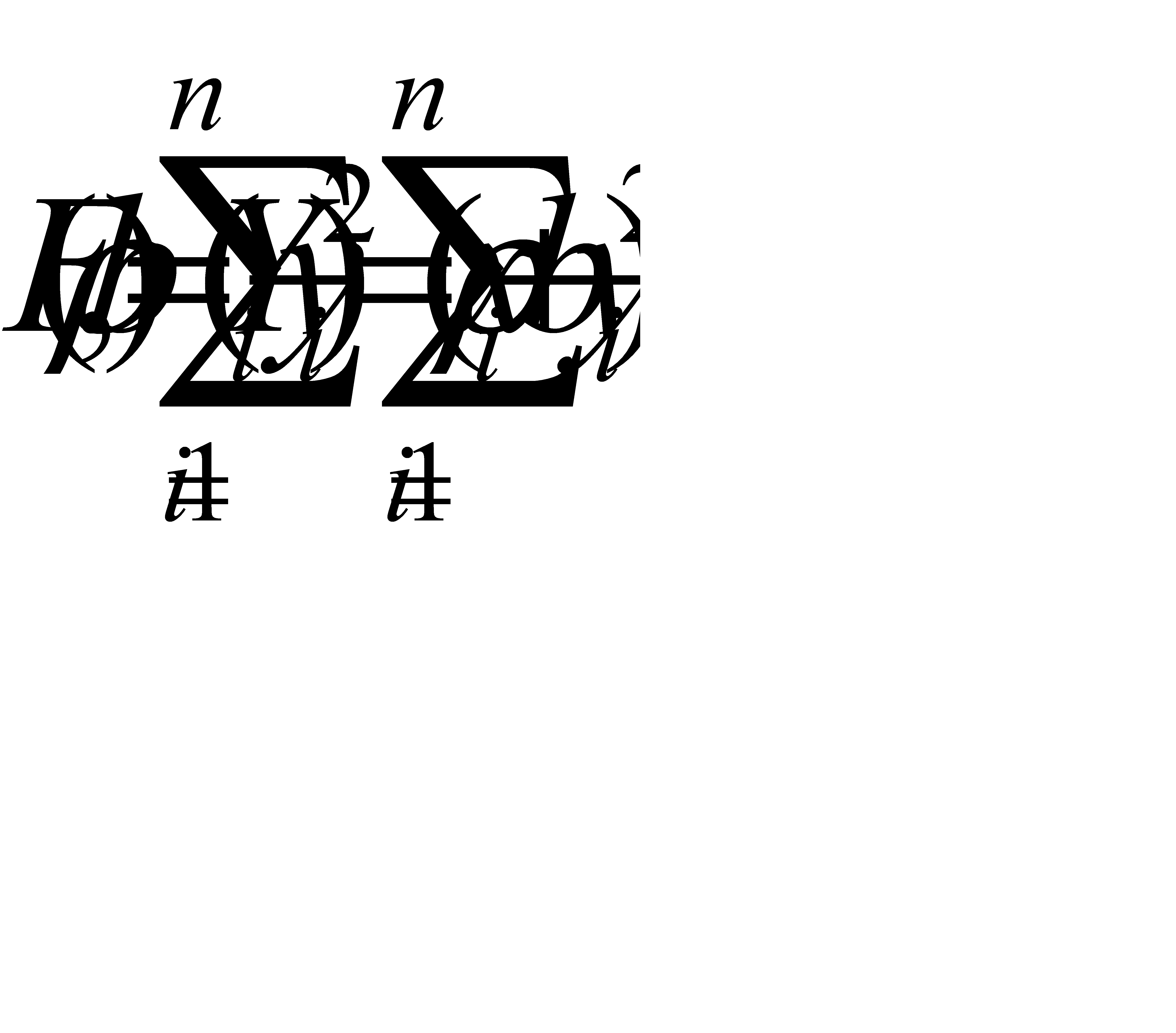 .
.
Приравняем нулю соответствующие частные производные:
 .
.
В результате получим систему двух линейных уравнений относительно ρ и b:

Ее решение позволяет найти искомые параметры в виде:
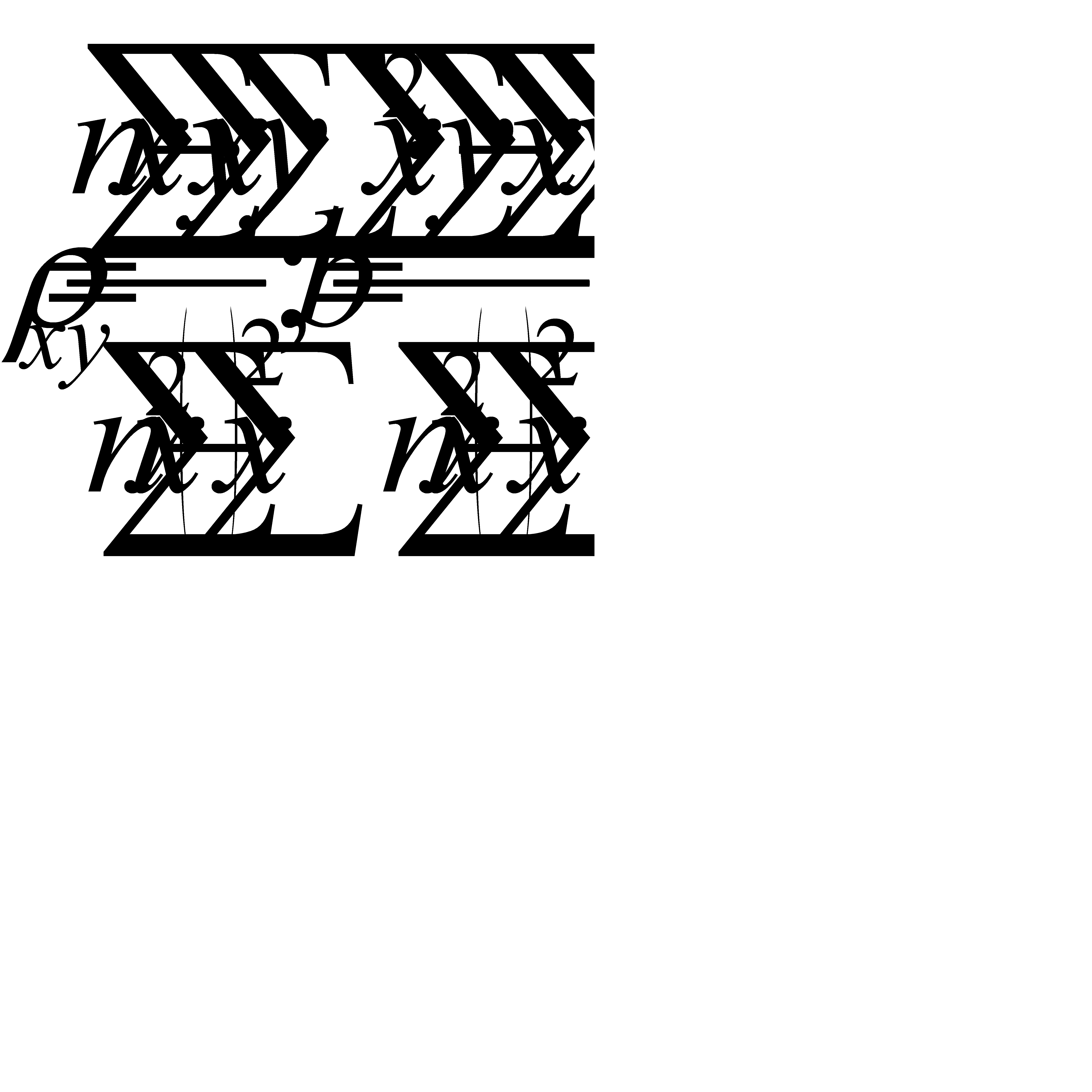 .
.
При этом предполагалось, что все значения Х и Y наблюдались по одному разу.
Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы:
| Y | X | ||||
| x 1 | x 2 | … | xk | ny | |
| y1 y 2 … ym | n 11 n 12 … n 1 m | n 21 n 22 … n 2 m | … … … … | nk 1 nk 2 … nkm | n 11+ n 21+…+ nk 1 n 12+ n 22+…+ nk 2 n 1 m +n 2 m +…+ nkm |
| nx | n 11+ n 12+…+ n 1 m | n 21+ n 22+…+ n 2 m | … | nk 1+ nk 2+…+ nkm | n= ∑ nx = ∑ ny |
Здесь nij – число появлений в выборке пары чисел (xi, yj).
Поскольку 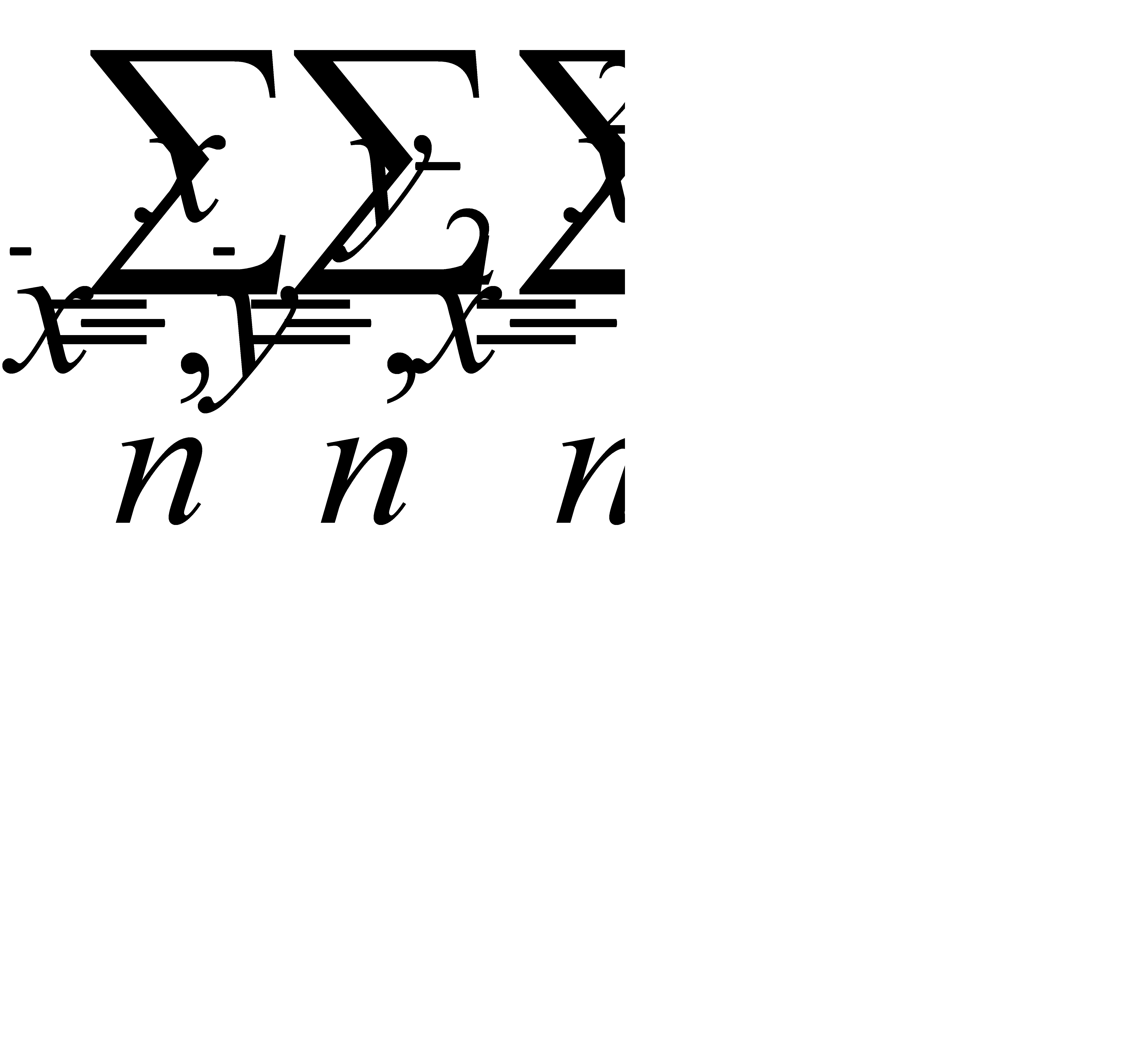 , заменим в системе (10.3)
, заменим в системе (10.3) 
 , где пху – число появлений пары чисел (х, у). Тогда система примет вид:
, где пху – число появлений пары чисел (х, у). Тогда система примет вид:
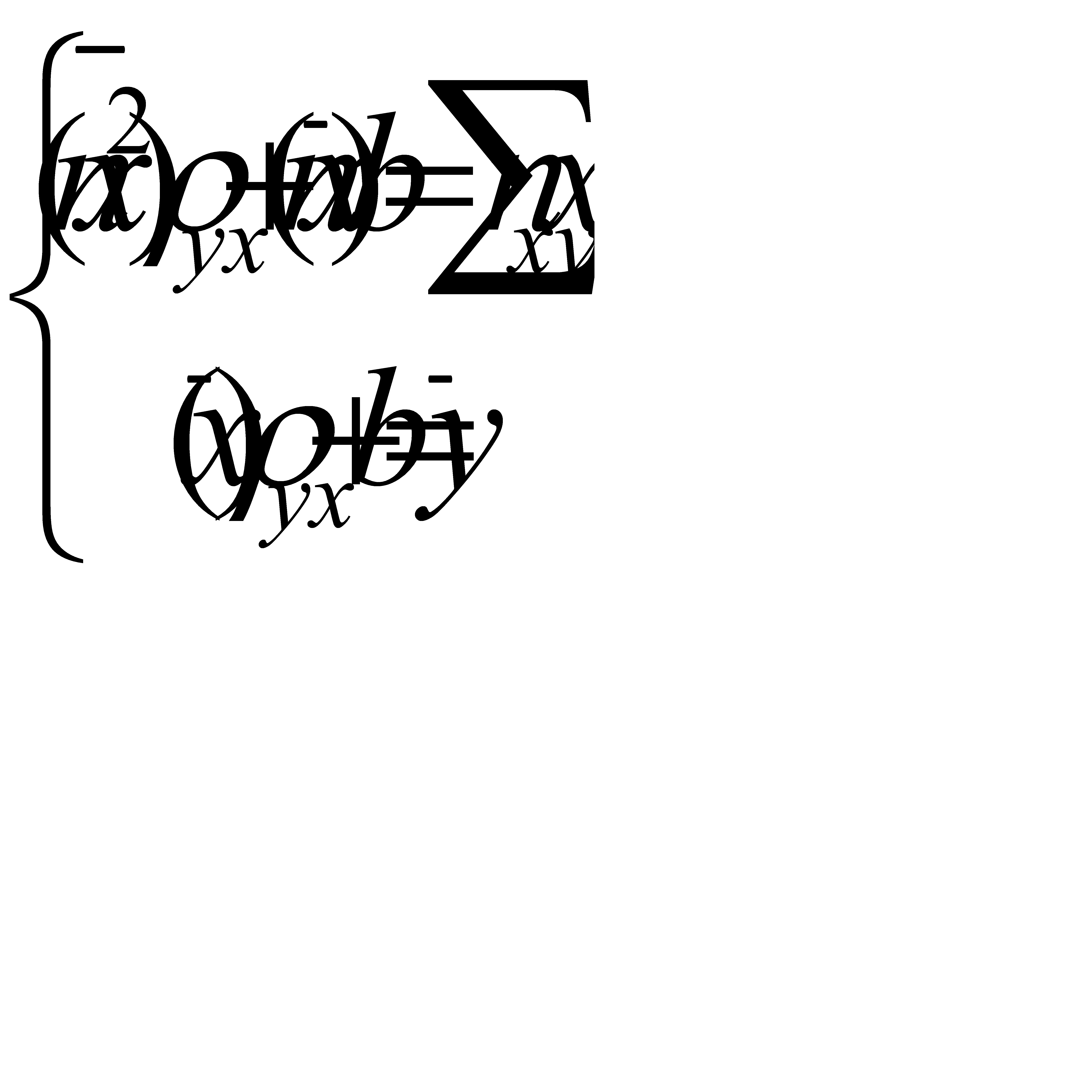
Можно решить эту систему и найти параметры ρух и b, определяющие выборочное уравнение прямой линии регрессии:
 .
.
Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы:
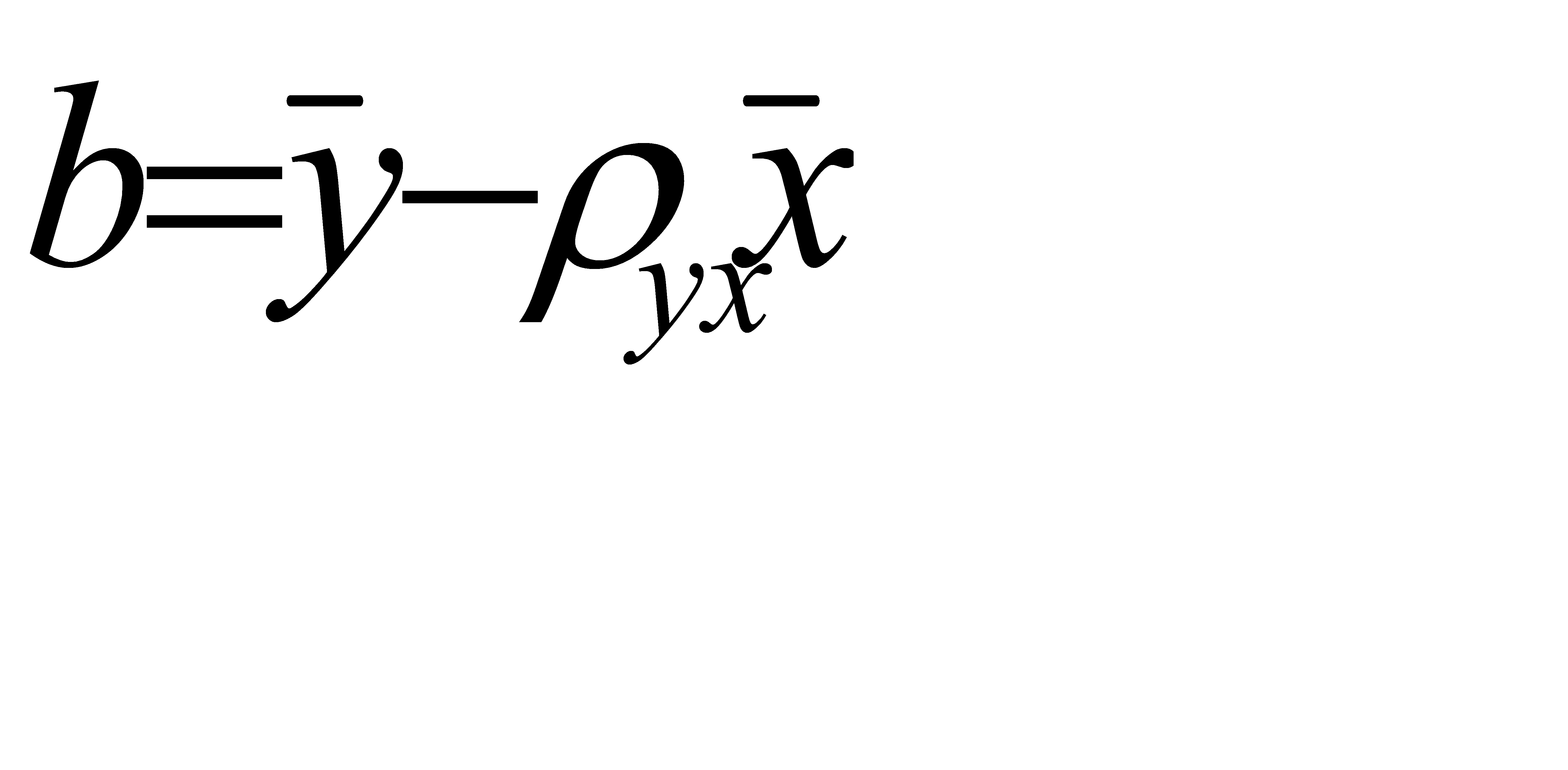 .
.
Подставим это выражение в уравнение регрессии:
 .
.
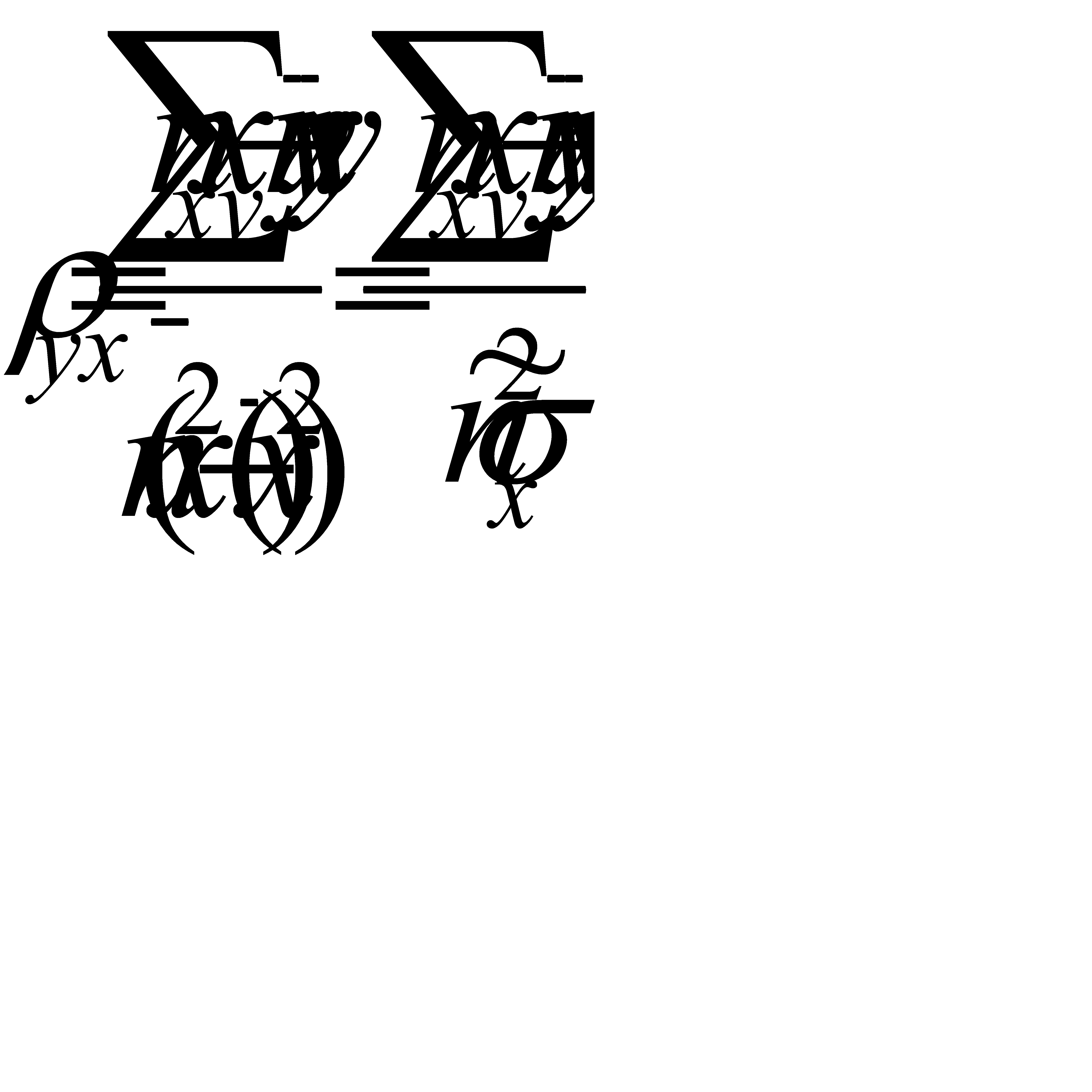 ,
,
где 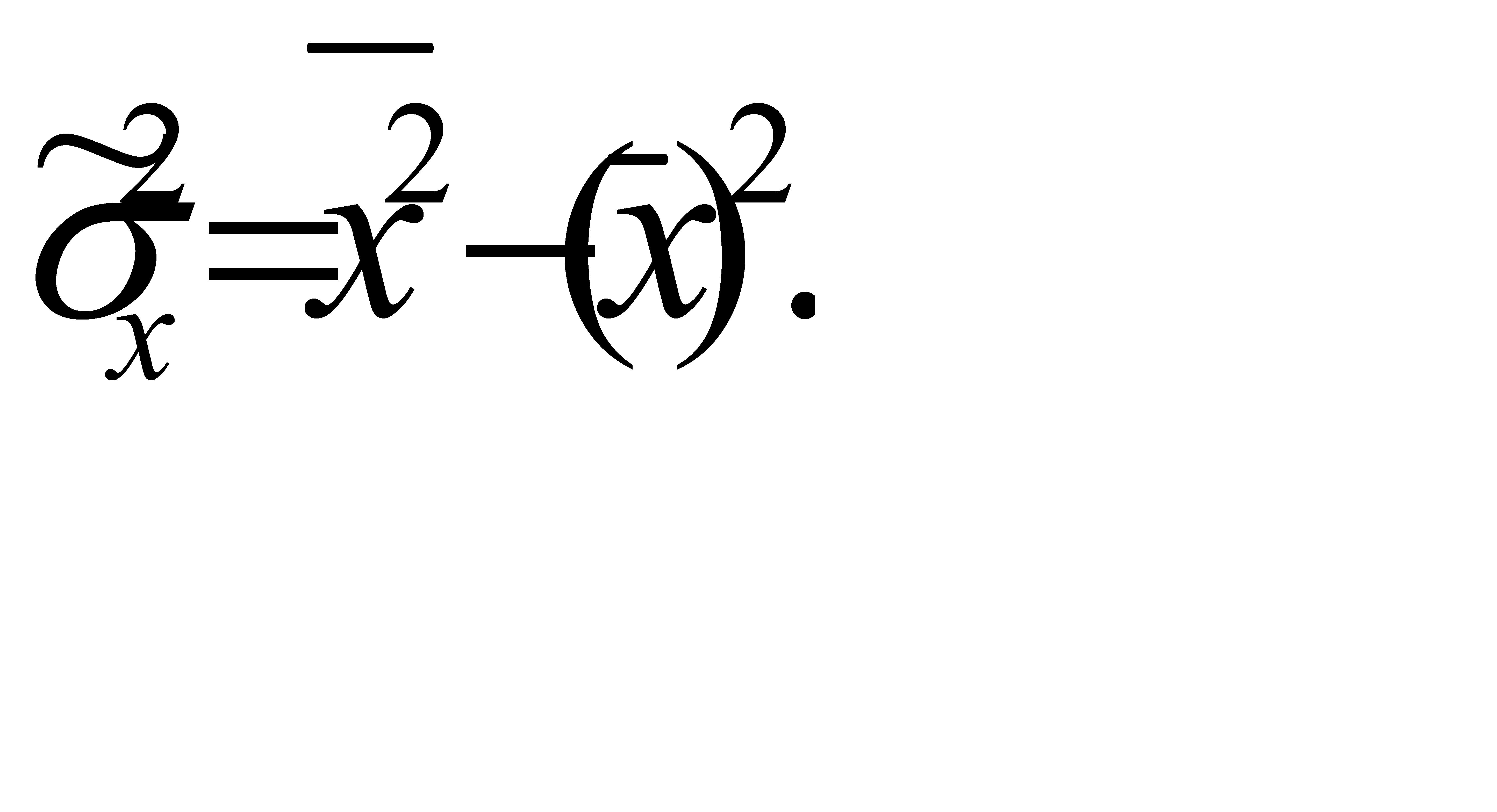
Введем понятие выборочного коэффициента корреляции

и умножим равенство на 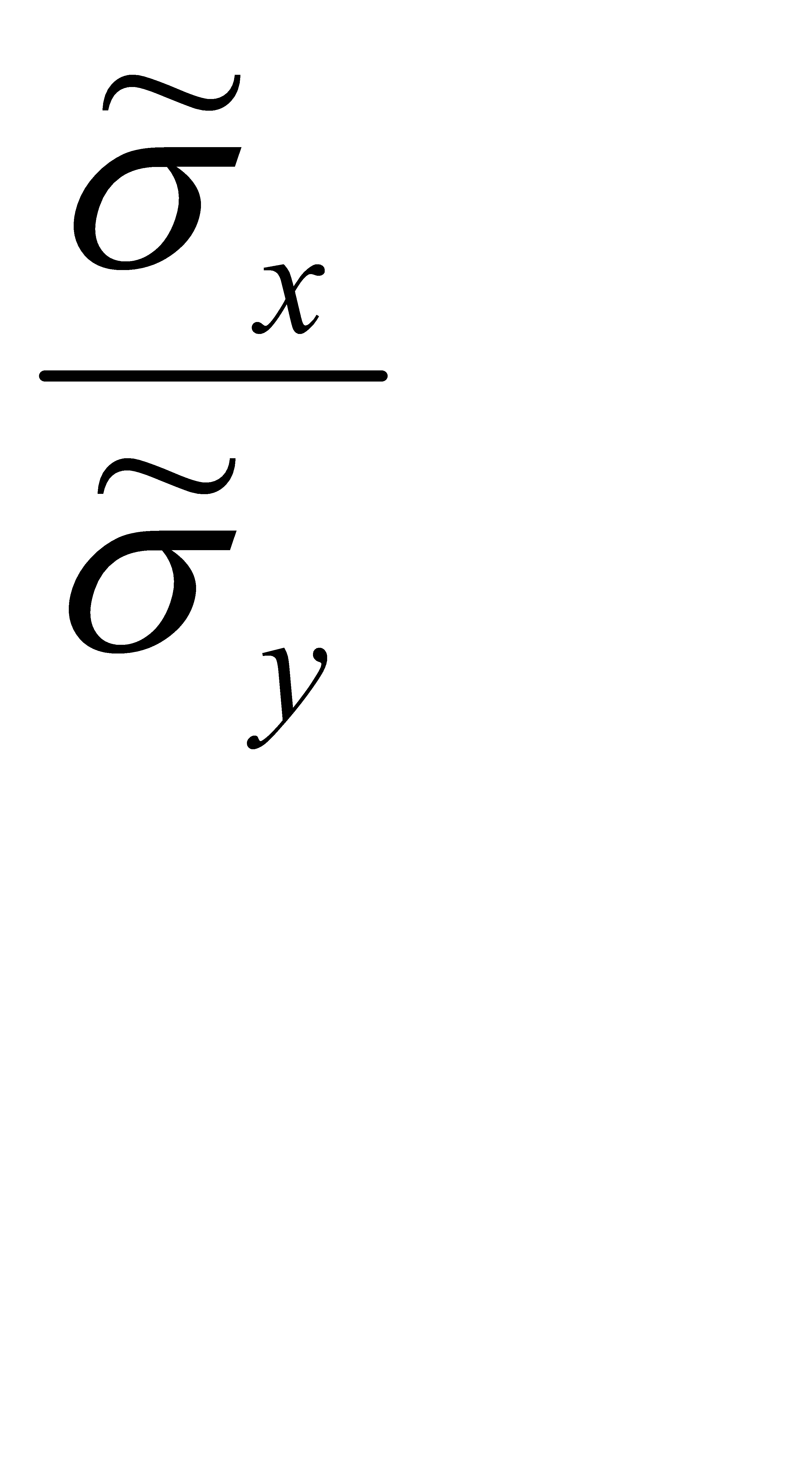 :
: 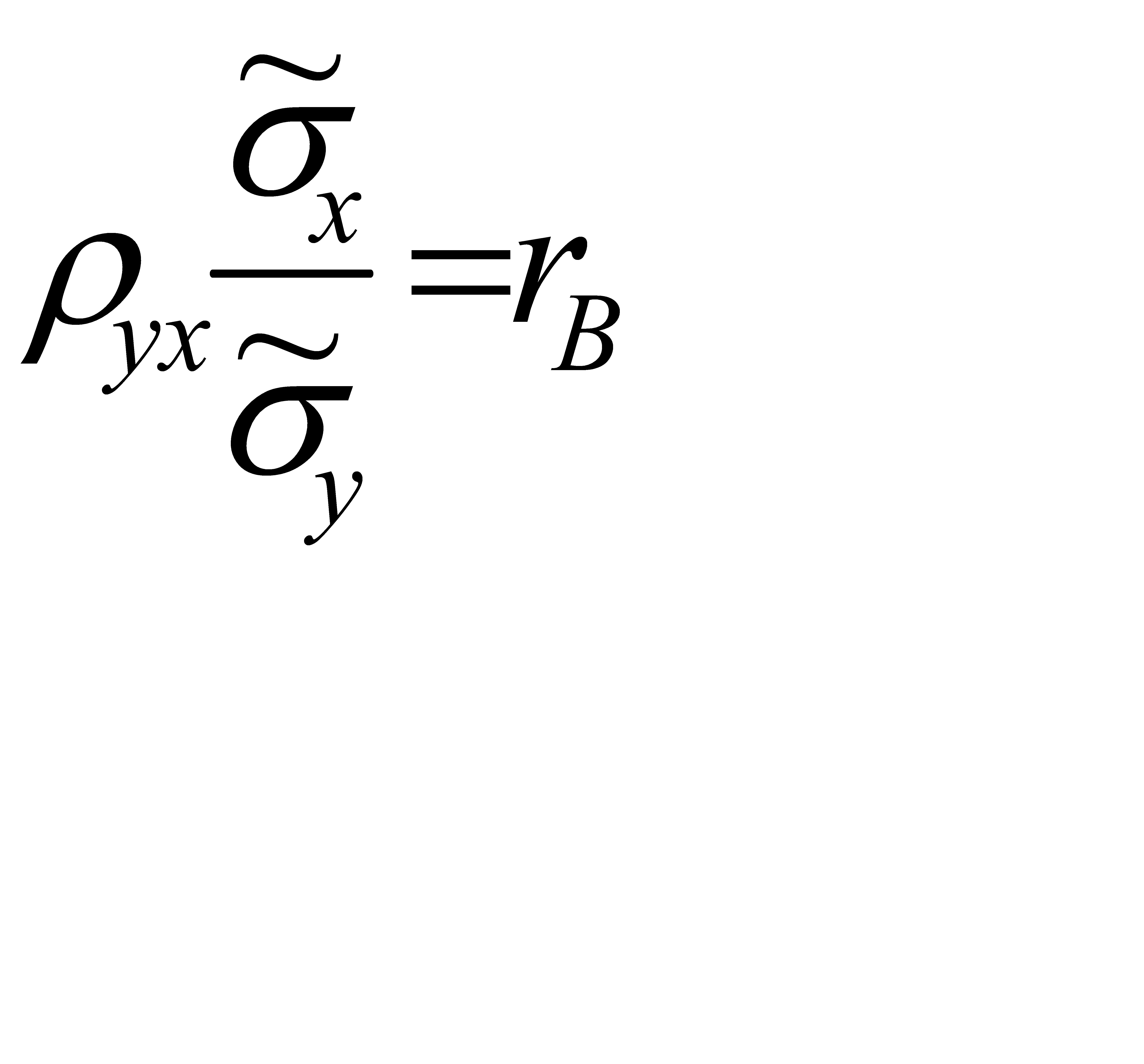 , откуда
, откуда  .
.
Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида
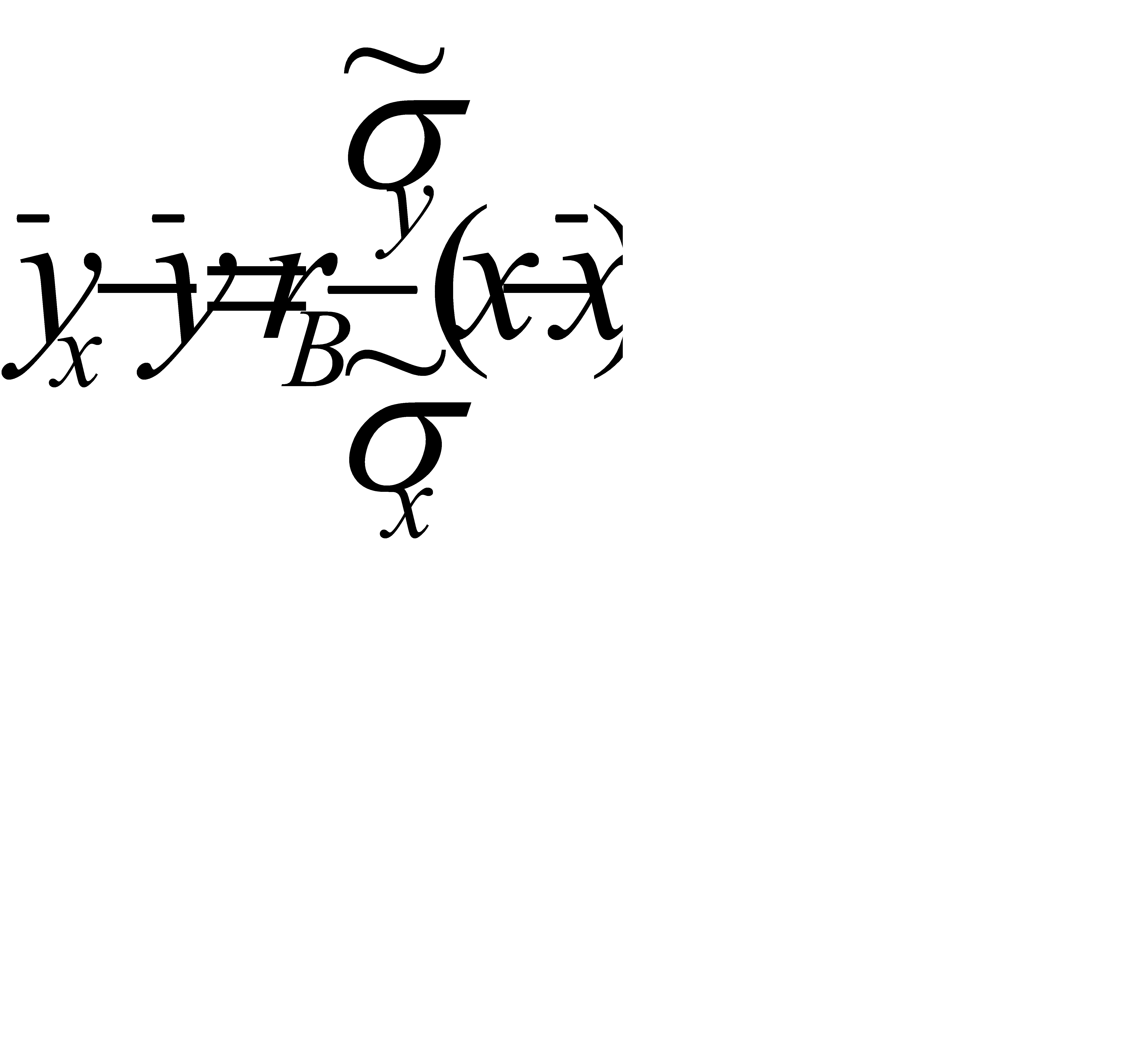 .
.
Типовая задача 2
Для 10 петушков леггорнов 15-дневного возраста были получены следующие данные о весе их тела 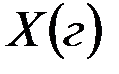 и весе гребня
и весе гребня 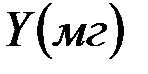 :
:
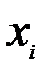
| ||||||||||
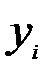
|
Требуется:
1) найти коэффициент корреляции и сделать вывод о тесноте и направлении линейной корреляционной связи между признаками;
2) составить уравнение прямой регрессии;
3) нанести на чертеже исходные данные и построить полученную прямую регрессии.
Дата публикования: 2015-10-09; Прочитано: 669 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
