Простейшие квадратурные формулы

Задача численного интегрирования возникает в прикладных исследованиях, когда значение определенного интеграла

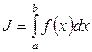(8)

не может быть вычислено аналитически, в частности, когда функция 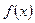задана таблицей своих значений.

Численное интегрирование выполняется с использованием так называемых квадратурных формул – приближенных равенств вида

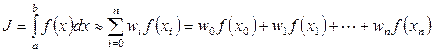, (9)

где - узлы квадратурной формулы; 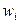- числовые коэффициенты, называемые весами квадратурной формулы; сумма 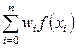, принимаемая за приближенное значение интеграла, называется квадратурной суммой; величина

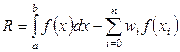(10)

называется погрешностью квадратурной формулы.

Распространенный способ построения квадратурных формул состоит в следующем. Интеграл (8) представляют в виде суммы интегралов по элементарным отрезкам :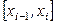

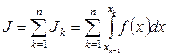. (11)

На каждом из элементарных отрезков функцию 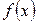аппроксимируют интерполяционным многочленом определенной степени и выполняют интегрирование (аналитически). Получаемые при этом формулы (для равноотстоящих узлов) называются формулами Ньютона – Котеса.

Если на элементарном отрезке 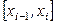длины 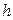использовать интерполяционный многочлен первой степени (3), то получим простейшую формулу Ньютона – Котеса – формулу трапеций:

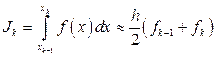. (12)

Для многочленов второй (4) и третьей (5) степени получим соответственно элементарные квадратурные формулы Симпсона

,

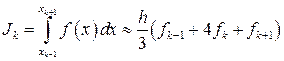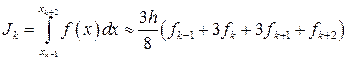, (13)

для интерполяционного многочлена четвертой степени - элементарную квадратурную формулу Буля

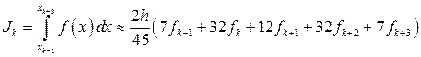. (14)

Если отрезок 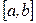разбит на 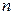элементарных интервалов 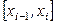длины 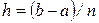равноотстоящими узлами, то, используя (11), (12), можно вывести составную формулу трапеций

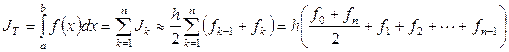. (15)

При записи составной формулы Симпсона следует брать четное число узлов; роль элементарного интервала играет интервал 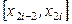, длины 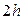, содержащий три узла. При 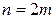эта формула имеет вид:

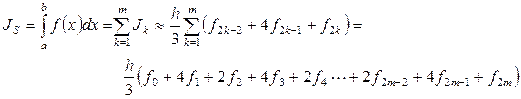(16)

Для составных квадратурных формул трапеций и Симпсона справедливы следующие оценки погрешностей:

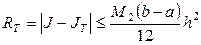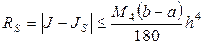, . (17)

Формула трапеций имеет второй порядок точности относительно 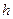, а формула Симпсона – четвертый; формула трапеций дает точный результат для многочленов первой степени, а формула Симпсона – для многочленов третьей степени.

Порядок выполнения задания

1. Задайте порядок интерполяционного многочлена; вычислите шаг, координаты узлов интерполяции и значения указанной в задании функции в узлах.

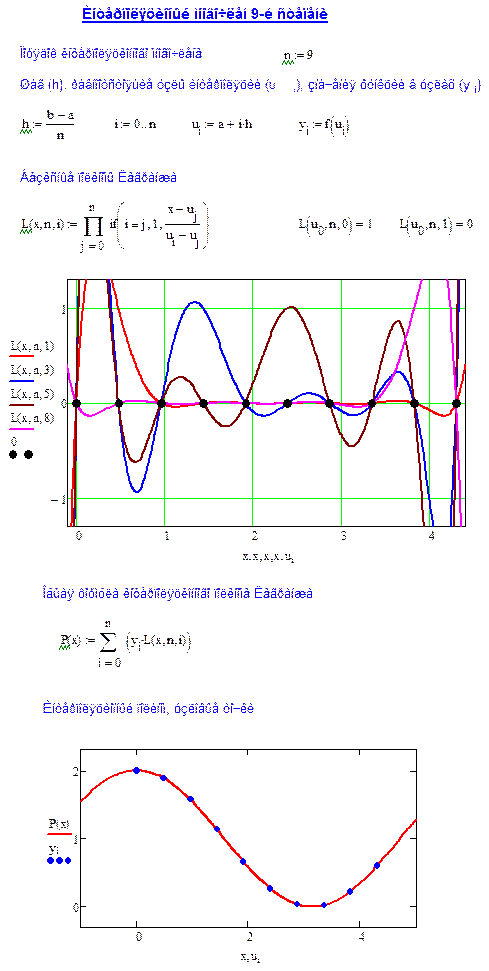
2. Запишите выражения для базисных полиномов, и постройте общую формулу интерполяционного многочлена Лагранжа.

3. Постройте график интерполяционного многочлена.

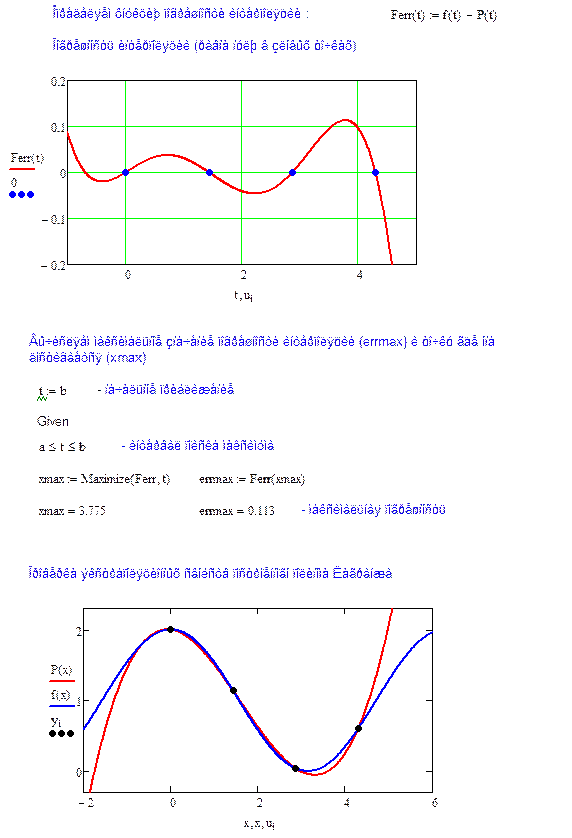
4. Определите функцию погрешности интерполяции и постройте ее график.

5. Вычислите максимальное значение погрешности интерполяции и определите точку, где это значение достигается.

6. Проверьте (визуально) экстраполяционные возможности многочлена Лагранжа, построив соответствующий график.

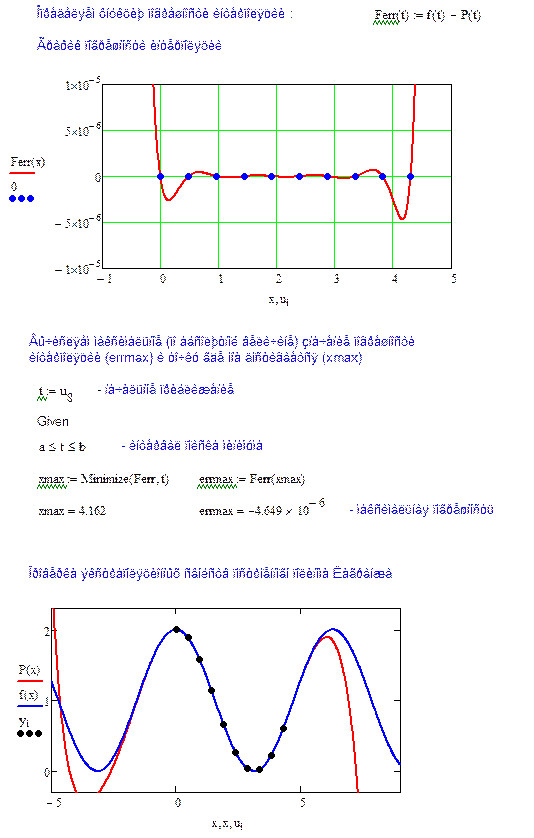
7. Увеличьте число интерполяционных узлов в три раза и повторите все предыдущие вычисления. Сравните результаты.

8. Выбрав определенное число интервалов интегрирования (в диапазоне от 4 до 10), вычислите координаты узловых точек и значения функции в этих точках.

9. Используя составную формулу трапеций, выполните численное интегрирование.

10. Выполните численное интегрирование с использованием составной формулы Симпсона. Сравните результаты.

11. Используя встроенные функции системы Mathcad, вычислите «точное» значение определенного интеграла и с его помощью погрешности формул трапеций и Симпсона.

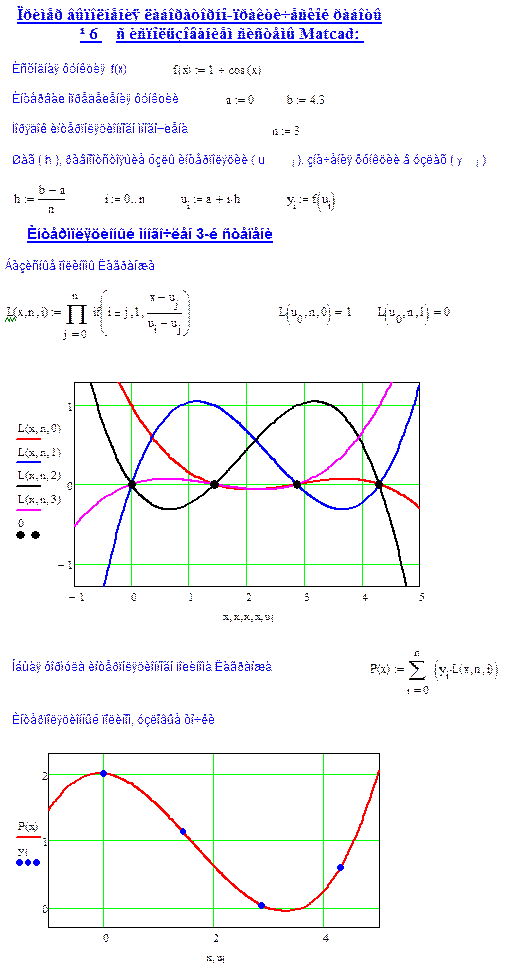
12. Повторите пункты 8 – 11 увеличивая всякий раз число интервалов интегрирования в 2 раза. На основе этих расчетов составьте таблицу погрешностей (5 – 10 строк). Анализируя табличные данные, сделайте определенный вывод о порядке точности формул Симпсона и трапеций.

13. Приведите оценку погрешности численного интегрирования, использую правило Рунге. Сравните эту оценку с теоретической оценкой.

14. Сделайте выводы по проделанной работе.

15. Сохраните рабочий документ.

При выполнении п.12 – 13 полезно построить графики, отражающие изменение погрешности (теоретической и полученной по правилу Рунге) численного интегрирования при последовательном удвоении количества узлов интегрирования.

При численном интегрировании по формуле трапеций можно воспользоваться одной из Mathcad-программ (объясните, в чем их отличие друг от друга):

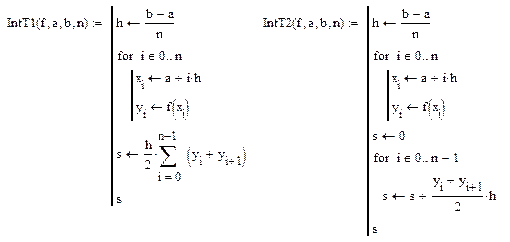
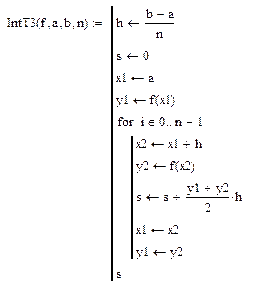
Далее можно использовать программу (J – точное значение определенного интеграла, вычисленное аналитически):

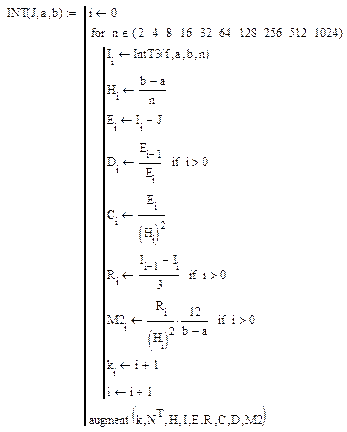
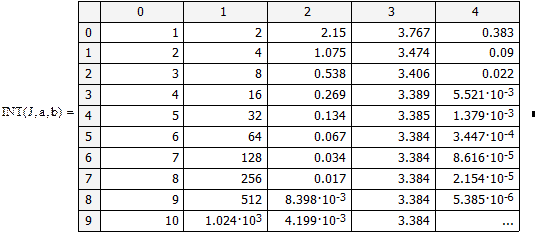
Аналогичные Mathcad-программы можно составить и для метода Симпсона.