 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интерполяционный полином Лагранжа
|
|
В наиболее общем виде задача интерполяции состоит в том, чтобы по значения функции в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, в столь общей постановке задача имеет не единственное решение. Задача становится более определенной, если в качестве интерполирующей функции рассматривать алгебраические многочлены.
Типичная практическая задача, приводящая к необходимости построения интерполяционного многочлена, состоит в следующем. В определенных точках (узлах) 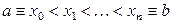 заданы экспериментально измеренные значения функции
заданы экспериментально измеренные значения функции  ; требуется вычислить значение этой функции в некоторой «промежуточной» точке
; требуется вычислить значение этой функции в некоторой «промежуточной» точке  , не совпадающей ни с одним из узлов
, не совпадающей ни с одним из узлов 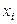 ; в частности, это может быть точка, где постановка эксперимента затруднена или вообще невозможна.
; в частности, это может быть точка, где постановка эксперимента затруднена или вообще невозможна.
Задача интерполяции состоит в построении функции  , график которой проходит через заданные точки
, график которой проходит через заданные точки 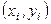 , т. е. выполняются условия
, т. е. выполняются условия
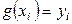 ,
, 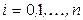 . (1)
. (1)
Располагая непрерывной функцией  , заданной аналитически, мы можем приближенно вычислить значение
, заданной аналитически, мы можем приближенно вычислить значение 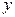 в любой точке
в любой точке  . Если
. Если  , то говорят об интерполяции, если же точка
, то говорят об интерполяции, если же точка  не принадлежит отрезку наблюдения
не принадлежит отрезку наблюдения 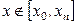 , то говорят об экстраполяции (прогнозе).
, то говорят об экстраполяции (прогнозе).
В качестве интерполирующей функции  обычно используются алгебраические многочлены. Доказано, что существует единственный интерполяционный многочлен степени
обычно используются алгебраические многочлены. Доказано, что существует единственный интерполяционный многочлен степени 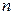 , удовлетворяющий условиям (1). Среди различных форм записи интерполяционного многочлена чаще всего используются запись в форме Лагранжа и в форме Ньютона. Подчеркнем, что они представляют собой различную запись одного и того же многочлена, удовлетворяющего условиям интерполяции (1).
, удовлетворяющий условиям (1). Среди различных форм записи интерполяционного многочлена чаще всего используются запись в форме Лагранжа и в форме Ньютона. Подчеркнем, что они представляют собой различную запись одного и того же многочлена, удовлетворяющего условиям интерполяции (1).
Интерполяционную формулу Ньютона можно рассматривать как разностный аналог формулы Тейлора. Ее удобнее применять в том случае, когда интерполируется одна и та же функция, но число узлов интерполяции постепенно увеличивается. Если же узлы интерполяции фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться формулой Лагранжа.
Рассмотрим полином Лагранжа, проходящий через 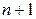 точку
точку 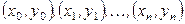 . Он имеет вид:
. Он имеет вид:
 , (2)
, (2)
где 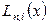 - базисные полиномы
- базисные полиномы
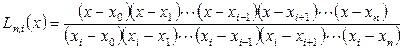 .
.
При каждом фиксированном значении 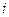 коэффициенты
коэффициенты 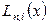 представляют собой многочлены степени
представляют собой многочлены степени 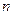 , обладающие свойством
, обладающие свойством
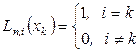 .
.
В силу этого свойства, в сумме (2) при 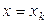 обращаются в нуль все слагаемые, кроме слагаемого с номером
обращаются в нуль все слагаемые, кроме слагаемого с номером 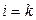 , равного значению
, равного значению  , и график полинома (2) проходит через все заданные точки
, и график полинома (2) проходит через все заданные точки 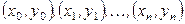 .
.
Приведем развернутые формулы для линейного, квадратичного и кубического полиномов Лагранжа:
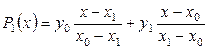 , (3)
, (3)
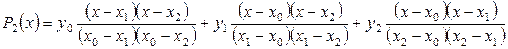 , (4)
, (4)
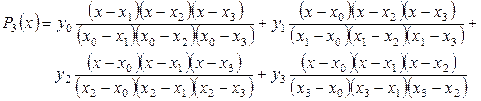 . (5)
. (5)
Для погрешности интерполяции 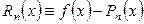 в общем случае справедливо утверждение: если функция
в общем случае справедливо утверждение: если функция 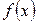 дифференцируема
дифференцируема 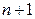 раз на отрезке интерполяции
раз на отрезке интерполяции 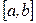 , то для погрешности в точке
, то для погрешности в точке 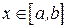 справедливо равенство
справедливо равенство
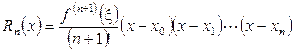 ,
, 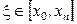 ,
,
где 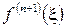 -
- 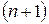 - я производная интерполируемой функции
- я производная интерполируемой функции 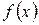 , вычисленная в некоторой точке
, вычисленная в некоторой точке 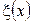 отрезка
отрезка 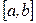 . Так как точка
. Так как точка 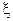 априори не известна, то обычно используют мажорантную оценку (оценку сверху)
априори не известна, то обычно используют мажорантную оценку (оценку сверху)
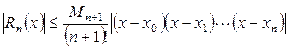 ,
, 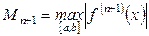 ,
,
и оценку максимума модуля погрешности
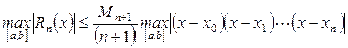 , (6)
, (6)
или более грубую оценку
 ,
, 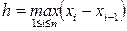 . (7)
. (7)
Приведенные оценки погрешности, что интерполяция многочленом степени 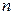 имеет
имеет 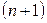 - й порядок точности относительно максимального шага таблицы
- й порядок точности относительно максимального шага таблицы 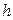 . В частности, формулы (3) - (5) имеют второй, третий и четвертый порядки точности соответственно.
. В частности, формулы (3) - (5) имеют второй, третий и четвертый порядки точности соответственно.
Важно помнить, что интерполяция полностью сохраняет или даже усиливает «шум» эксперимента. Поэтому операция интерполирования применяется только в тех задачах, где ошибки эксперимента малы, и ими можно пренебречь.
Дата публикования: 2015-10-09; Прочитано: 404 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
