Признаки косого параллелограмма

Теорема. (Первый признак косого параллелограмма) Для того, чтобы косой четырехугольник был косым параллелограммом, необходимо и достаточно, чтобы каждая из его диагоналей образовала со сторонами четырехугольника пару равновеликих треугольников.

Рисунок 2.4

Доказательство:

Пусть АВСD- косой параллелограмм, АС,BD – его диагонали (рис 2.4). Проведем высоты ВВ₁ и DD₁ треугольников АВС и ACD. Из середины N диагонали BD опустим на АС перпендикуляр NN₁. Поскольку BN=ND, то B₁N₁=N₁D₁. Следовательно, BN₁=N₁D и поэтому NN₁ ^ BD. Таким образом, NN₁-общий перпендикуляр диагоналей АС и BD. Если из середины М диагонали АС опустим перпендикуляр ММ1 на BD, то аналогичным образом рассматривая пару равновеликих треугольников, доказываем, что ММ1- общий перпендикуляр этих диагоналей. Но две скрещивающиеся прямые имеют только один общий перпендикуляр, поэтому ММ₁=NN₁. Другими словами, общий перпендикуляр проходит через середины диагоналей и служит для косого четырехугольника осью симметрии. Это значит, что ABCD-косой параллелограмм.

Теорема. (Второй признак косого параллелограмма) Для того, чтобы косой четырехугольник был косым параллелограммом, необходимо и достаточно, чтобы прямая, проходящая через центр сферы, описанной около тетраэдра (вершины которого совпадают с вершинами четырехугольника), и через центр сферы, вписанной в этот тетраэдр, пересекала диагонали четырехугольника.

Доказательство:

Пусть прямая, проходящая через центр J сферы, вписанной в тетраэдр ABCD, пересекает диагонали AC и BD соответственно в точках P и Q, принадлежащим соответственно отрезкам AC и BD. Докажем, что если на прямой PQ лежит центр О сферы, описанной около тетраэдра ABCD, то ABCD- косой параллелограмм.

В самом деле, плоскость, проходящая через AC и Q, является биссектрисой для двугранного угла тетраедра при ребре AC. Следовательно, каждая ее точка, в том числе и О, одинаково удалена от граней АВС и ACD. Поэтому окружности, описанные около треугольников ABC и ACD, равны. Отсюда уже следует, что ÐАВС=Ð ADC или ÐАВС+ÐADC=p. Если центр О сферы лежит внутри отрезка PQ или на его продолжении за точку Q, то центры окружностей, описанных около треугольников АВС и АСD, лежат соответственно с вершинами B и D по одну сторону от АС и ÐАВС=ÐADC. Если же центр О лежит на продолжении отрезка PQ за точку Р, то центры окружностей, описанных около треугольников АВС и ACD, находятся с вершинами B и D этих треугольников по разные стороны от АС и снова ÐАВС=ÐADC. Следовательно, случай, когда ÐАВС+ÐADC=p, отпадает. Аналогичным образом доказываем, что ÐBCD=ÐBAD. Но согласно теореме из пункта 2.3 четырехугольник ABCD –косой параллелограмм.

3.КОСОЙ ЧЕТЫРЕХУГОЛЬНИК В ПРИМЕРАХ И ЗАДАЧАХ

Задача 1

Даны четыре прямые, никакие три из которых не компланарны, тогда существует косой четырехугольник, стороны которого параллельны этим прямым.

Доказательство:

Пусть - векторы, параллельные данным прямым. Так как любые три прямые из данных не компланарны, то их направляющие векторы так же не компланарны, таким образом они образуют базис. Тогда четвертый направляющий вектор может быть представлен как их линейная комбинация, то есть разложен по векторам базиса.

Возьмем в качестве базисных векторов , тогда

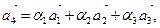
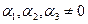
или

.

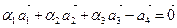Легко видеть, что на векторах 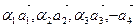можно построить косой четырехугольник.

Задача 2

а) Сколько существует попарно не равных пространственных четырехугольников с одним и тем же набором векторов?

б) Докажите, что объем всех тетраэдров, заданных этими пространственными четырехугольниками, равны.

Решение:

а) Если заданы стороны пространственного четырехугольника в виде векторов 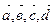, то сумма всех этих векторов должна быть равной нулю. Если от А отложить 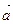, то В является концом 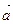,от которого можно отложить три вектора 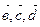. Значит существуют три варианта выбора второго вектора. Если второй вектор выбран, то третий можно выбрать двумя способами. То есть вариантов выбора трех векторов существует 3×2=6. Последний вектор можно выбрать только одним способом.

Значит всего 6 попарно не равных пространственных четырехугольников с одним и тем же набором векторов.

б) Пусть а,b,c и d – данные векторы сторон. Рассмотрим параллелепипед, задаваемый векторами а,b и c (рис. 3.1); его диагональю служит вектор d. Несложный перебор показывает, что все шесть различных четырехугольников содержатся среди четырехугольников, сторонами которого являются ребра этого параллелепипеда и его диагональ d (фиксировать при переборе удобно вектор d). Объем каждого соответствующего тетраэдра составляет 1/6 часть объема параллелепипеда.

Рисунок 3.1

Задача 3

Пусть в пространстве задан тетраэдр А₁А₂А₃А₄.

а) Доказать, что любая точка Х имеет некоторые барицентрические координаты относительно него.

б) Доказать, что при условии m ₁+ m ₂+ m ₃+ m ₄=1 барицентрические координаты точки Х определены однозначно.

Решение:

Рисунок 3.2

а) Введем следующие обозначения:

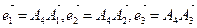и .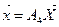

Точка Х является центром масс вершин тетраэдра А₁А₂А₃А₄ (рис.3.2) с массами m₁,m₂,m₃,m₄ тогда и только тогда, когда

то есть

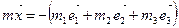, (3.1)

где m=m ₁ +m ₂ +m ₃ +m ₄.

Будем считать, что m =1 в (3.1).

б) Докажем однозначность барицентрических координат. Любой вектор 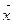можно представить в виде

,

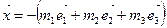причем числа m ₁, m ₂, m ₃ определены однозначно. Число m ₄ находится по формуле:

m ₄ = 1 -m ₁ - m₂ -m ₃,

то есть определена также однозначно.

Задача 4

В системе барицентрических координат, связанных с тетраэдром А₁А₂А₃А₄.

Найти уравнение:

а) прямой А₁А₂;

б) плоскости А₁А₂А₃;

в) плоскости, проходящие через А₃А₄ параллельно А₁А₂.

Решение:

а) Пусть точка О - полюс системы барицентрических координат, точка М(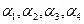) – произвольная точка (А₁А₂), тогда

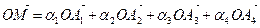
(из определения барицентрических координат).

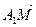êê , = ,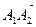

, ,

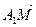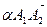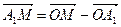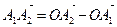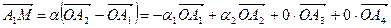
или

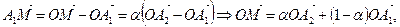
то есть , , .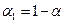

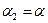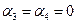Точка с барицентрическими координатами 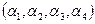лежит на прямой 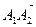, если 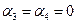. Таким образом векторное уравнение (А₁А₂) имеет вид

.

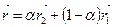б) Пусть точка М принадлежит (А₁А₂ А₃), тогда

.

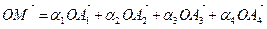Воспользуемся геометрическим смыслом барицентрических координат. Получаем

.

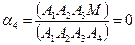Точка М лежит в плоскости (А₁А₂А₃ ), если 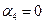. Таким образом векторное уравнение плоскости имеет вид

.

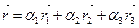в) Пусть:

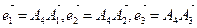- базис.

Для точки 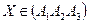, такой что 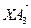çç 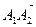, можно записать

.

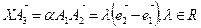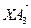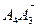и образуют базис плоскости (А₄ХА₃), тогда для любой точки этой плоскости

, .

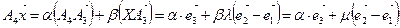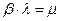Решим задачу при помощи барицентрических координат.

Вводим базис 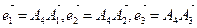. Тогда

.

, ,

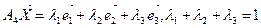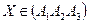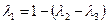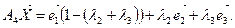
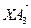çç ,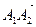

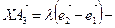с одной стороны.

С другой стороны

.

В силу единственности разложения вектора, получаем

,

.

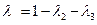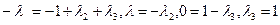Задача 5

Доказать, что если точка с барицентрическими координатам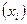и и принадлежат некоторой прямой, то той же прямой принадлежит точка с координатами .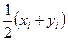

Решение:

Пусть точки А (х₁,х₂,х₃,х₄) и В (y₁y₂y₃y₄) заданы барицентрическими координатами. Тогда 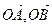(О-полюс) имеют те же координаты.

Отсюда

.

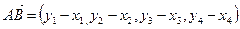Условие 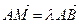является условием принадлежности точки М(z₁,z₂,z₃,z₄) прямой АВ. Приравнивая координаты получим:

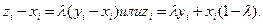
При 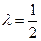получаем интересующее равенство.

Задача 6

Пусть 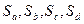- площади граней DCD, ACD, ABD и ABC тетраэдра ABCD. Найти координаты центра вписанной сферы.

Решение:

Пусть точка Р- центр сферы с барицентрическими координатами (l₁,l₂,l₃,l₄), тогда используя метрический смысл барицентрических координат, получим:

,

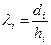причем, d_i =R (радиус сферы). С другой стороны

,

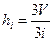то есть

,

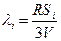тогда

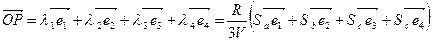
Точка Р имеет координаты .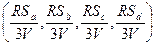

Задача 7

Поставим задачу определить расстояние между точками М и Р если известны барицентрические координаты l_i точки Р и расстояния 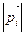точки М от вершин А_i данного тетраэдра.

Решение:

Пусть l_i- барицентрические координаты точки Р относительно тетраэдра А₁А₂А₃А₄. Тогда для любого вектора 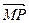имеет место равенство:

,где 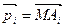. (3.2)

При любом выборе точки О в качестве полюса

.

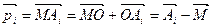Поэтому

,

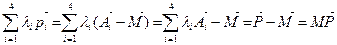
так как l₁+l₂+l₃+l₄=1.

Вычислим скалярный квадрат вектора 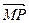. Воспользовавшись равенством (3.2), будем иметь:

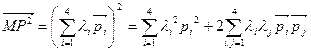, i<j.

Но

,

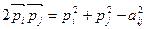поэтому

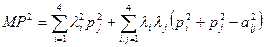, i<j

После несложных преобразований находим, что

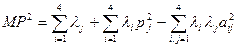, i<j

и окончательно

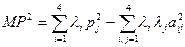, i<j. (3.3)

Задача 8

Используя решение предыдущей задачи определим расстояние между некоторыми замечательными точками тетраэдра.

Решение:

1) Пусть точка М совпадает с центром О описанной около тетраэдра сферы. Если R-радиус сферы, то все 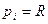. Точку Р поместим в центроид G тетраэдра. Для нее 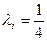. Согласно (3.3) будем иметь:

, i<j (3.4)

Из (3) следует, что для всякого тетраэдра имеет место неравенство:

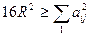, i<j,

причем знак неравенства следует писать тогда и только тогда, когда центроид и центр описанной сферы совпадают.

2) Если точка G- центроид тетраэдра, а точка М совпадает с одной из вершин тетраэдра, например, с вершиной А₄, то 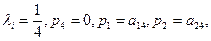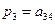и равенство (3.3) в этом случае принимает вид:

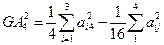,i<j,

или

.

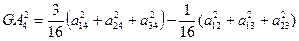Учитывая, что где G_i – центроид грани 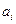, отсюда получаем формулу для вычисления длины медианы тетраэдра через длины его ребер:

.

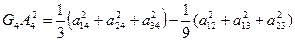Задача 9

Пусть точка Р- точка, не лежащая на сторонах косого четырехугольника А₁А₂А₃А₄, через которую проведены две прямые, пересекающие попарно различные его противоположные стороны, соответственно в точках Р₁₂, Р₃₄ и Р₂₃, Р₄₁ (рис. 3.3), а так же заданы отношения, в которых они делят соответствующие стороны

.

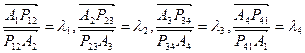По теореме Менелая для А₁А₂А₃А₄ 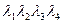=1.

Найти в каком отношении делит точка Р отрезки Р₁₂Р₃₄ и Р₂₃Р₄₁, то есть

.

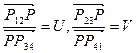Рисунок 3.3

Решение:

1) Рассмотрим косой четырехугольник Р₁₂А₂А₃Р₃₄ и плоскость А₁Р₁₄А₄Р₂₃ (рис.3.3). По теореме Менелая:

,

,

, ,

, ,

,

,

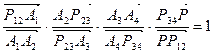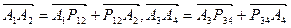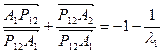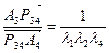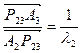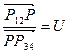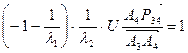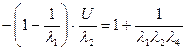, умножим на l₁l₂,

,

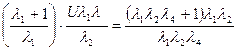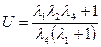(3.5)

2) Рассмотрим косой четырехугольник Р₁₄А₁А₂Р₂₃ и плоскость А₃Р₃₄А₄Р₁₂. По теореме Менелая:

,

, ,

,

,

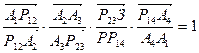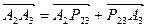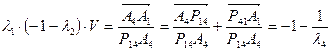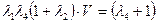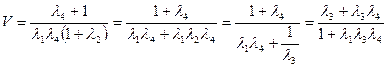. (3.6)

Замечание: Легко видно, что для определения U или V достаточно знать только три из l₁,l₂,l₃,l₄ (четвертое всегда находится из 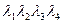=1).

Если сделать замену в (3.5) и (3.6) соответственно:

l₁=l, l₂=y, 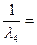х;

, , ,

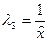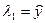то получим:

U= 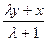, V= .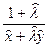

Задача 10

Для любых косых параллелограммов, стороны которых попарно параллельны, отношения соответствующих сторон равны.

Доказательство:

Пусть А₁А₂А₃А₄, В₁В₂В₃В₄- косые параллелограммы, удовлетворяющие условию задачи. ↑↑ .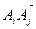

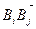Для В₁В₂В₃В₄

.

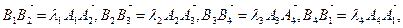
Из определения косого параллелограмма следует, что 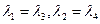. Разделив на 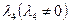получаем

, .

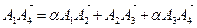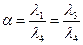Для А₁А₂А₃А₄

.

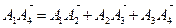Получаем, что 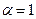в силу единственности разложения вектора по базису.

Значит .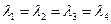

ВЫВОДЫ

В квалификационной работе, на основе проведенного анализа теоретического и практического материала по теме «Метрические свойства косого четырехугольника», в трех разделах изложен с единой точки зрения систематизированный материал. В первых двух разделах изложен теоретический материал и в третьем разделе приведены задачи с решениями.

Формулировки большинства задач взяты из сборников [3,17,20], а остальные сформулированы автором. Основная часть приведенных решений и доказательств задач также принадлежит автору.

Цель квалификационной работы достигнута.

Материалы квалификационной работы могут быть использованы как составная часть факультативного курса по геометрии для учащихся 10-11 классов, а также как спецкурс для студентов математических специальностей.