Перемножим эти равенства

,

.

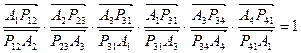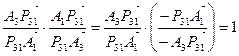Получили доказываемое соотношение (1.11).

Достаточность. Пусть равенство (1.11) выполняется. Тогда по теореме Менелая для косого четырехугольника А₁А₂А₃А₄, точки Р₁₂,Р₂₃,Р₃₄, Р₄₁ лежат в одной плоскости. Это значит, что прямые Р₁₂Р₃₄ и Р₂₃Р₄₁ пересекаются в некоторой точке Р. Следовательно, плоскости А₁Р₂₃А₄, Р₁₂А₃А₄, А₁А₂Р₃₄, А₂А₃Р₄₁ проходят через точку Р.

Следствие. если точки Р₁₂,Р₂₃,Р₃₄, Р₄₁, взятые на прямых A₁A₂, А₂А₃, А₃А₄, А₄А₁, лежат в одной плоскости, то плоскости Р₁₂А₃А₄, Р₂₃А₄А₁, Р₃₄А₁А₂, Р₄₁А₂А₃ пересекаются в одной точке, и обратно.

Теорема Гаусса. Пусть плоскость, не проходящая через вершины косого четырехугольника А₁А₂А₃А₄, пересекает его стороны соответственно в точках Р₁₂,Р₂₃,Р₃₄, Р₄₁. Тогда центроиды треугольников Р₁₂А₃А₄, Р₂₃А₄А₁, Р₃₄А₁А₂, Р₄₁А₂А₃ принадлежат одной плоскости.

Рисунок 1.6

Доказательство:

Пусть А₁А₂А₃А₄- косой четырехугольник. Обозначим центроиды треугольников Р₁₂А₃А₄, Р₂₃А₄А₁, Р₃₄А₁А₂, Р₄₁А₂А₃ через G_ij (соответственно точкам P_ij), а отношения 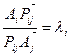(рис.1.6). Договоримся радиус-векторы точек обозначать одной буквой. Тогда радиус-векторы точек G_ij определяются

, ,

, .

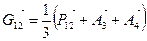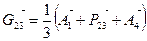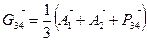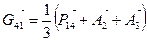Пользуясь (1.10), имеем

.

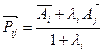Тогда

, ,

,

.

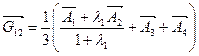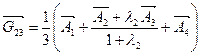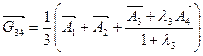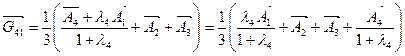Матрица нормированных барицентрических координат точек G_ij относительно тетраэдра А₁А₂А₃А₄ (после сокращения на 1/3) имеет вид:

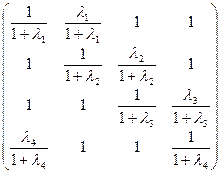
Для нахождения ранга этой матрицы, после преобразований ее столбцов приходим к матрице вида

.

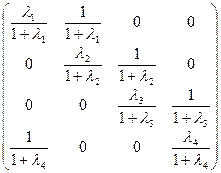Эта матрица сходна с матрицей 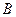(из доказательства теоремы Менелая) и тем же путем, что и 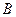приводится к виду 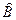. Но так как точки Р_ij лежат по условию в одной плоскости, то по теореме Менелая 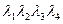=1 и поэтому ранг нашей матрицы равен трем, что и доказывает теорему.

2 ЗАВИСИМОСТЬ МЕЖДУ УГЛАМИ, СТОРОНАМИ И ДИАГОНАЛЯМИ КОСОГО ЧЕТЫРЕХУГОЛЬНИКА.

КОСОЙ ПАРАЛЛЕЛОГРАММ