Прямые и плоскости разного числа измерений

Параллельные прямые определяются в многомерном пространстве так же, как в трехмерном, и так же доказываются теоремы:

1.Через точку, не лежащую на данной прямой, проходит прямая, ей параллельная, и притом только одна.

2.Две прямые, параллельные одной и той же прямой, параллельны друг другу.

Для определения параллельности воспользуемся понятием о параллельном переносе. Он определяется буквально так же, как на плоскости или трехмерном пространстве. Это отображение, при котором точки X переходят в такие точки Y, что все векторы 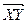равны.

Теперь даем определение. Прямые и плоскости параллельны, если одна переводится в другую переносом. Прямая параллельна плоскости, если она не лежит в этой плоскости, но ее можно отобразить в эту плоскость переносом.

Общее понятие плоскости. Если пространство более чем трехмерное (не выполняется аксиома пересечения плоскостей), то в нем наряду с обычными двумерными плоскостями есть другие фигуры, также называемые плоскостями.

Определение. Плоскостью, вообще, называется такая фигура, которая содержит по крайней мере три точки, не лежащие на одной прямой, и вместе с каждыми двумя своими точками содержит всю содержащую их прямую, но при этом не является всем пространством. Обычная двумерная плоскость, очевидно, подпадает под это определение.

Теорема. Всякая недвумерная плоскость представляет собой евклидово пространство, т. е в ней выполняются аксиомы, определяющие евклидово пространство, с теми же двумерными плоскостями, какие имеются в объемлющем пространстве.

Через всякие три точки любой данной плоскости проходит содержащаяся в ней двумерная плоскость.

Доказательство. Пусть P – данная плоскость в каком-либо евклидовом пространстве и А, В, С – какие-либо три ее точки. По определению плоскости она содержит прямую АВ, но не сводится к ней. Поэтому если точка С оказалась на этой прямой, то можно взять точку D, не лежащую на прямой АВ. Если С не лежит на АВ, то D и есть С.

Плоскость P, по ее определению, содержит прямые АВ и AD. Через эти прямые проходит двумерная плоскость Q, образованная пересекающими их прямыми. Все эти прямые будут содержаться в плоскости Р (в силу определения плоскости). Следовательно, в Р содержится двумерная плоскость Q, проходящая через данные точки А, В, С, что и требовалось доказать.

Итак, первая аксиома евклидова пространства выполнена. Вторая выполняется очевидно, поскольку она выполняется в объемлющем пространстве для любых двух плоскостей с двумя общими точками.

Число измерений плоскости можно определить, как в пространстве, числом взаимно перпендикулярных прямых. Прямую можно считать одномерной плоскостью.

Плоскость Р можно назвать параллельной плоскости Q, если существует перенос, перемещающий ее в плоскость Q, т. е. такой перенос t, что 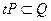. Мы пишем: 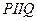(но это значит, что 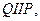только если 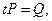так что перемещается в Р обратным переносом ).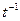

В четырехмерном пространстве есть трехмерные плоскости: каждая из них – это трехмерное евклидово пространство. Если две такие плоскости имеют общую точку, то их пересечение представляет двумерную плоскость.