Приближенное вычисление определенного интеграла

В настоящем пункте рассматриваются способы приближенного вычисления определенных интегралов

Введем на [а, в] равномерную сетку с шагом h, т.е. множества точек

и представим интеграл в виде суммы интегралов по частным отрезкам:

Для построения формулы численного интегрирования на всем отрезке [а, в] достаточно построить квадратичную формулу для на частном отрезке [х_i-1, х_i].

2.1. Формула прямоугольников. Заменим интеграл S_i выражением Геометрический такая замена означает, что площадь криволинейной трапеции АВСД заменяется площадью прямоугольника АВС₁Д₁ (см. рис. 3).

Рис. 3

Тогда получим формулу

(26)

которая называется формулой прямоугольников на частичном отрезке [х_i-1, х_i].

Погрешность метода (26) определяется величиной

которую легко оценить с помощью формулы Тейлора. Действительно, запишем ψ_i в виде

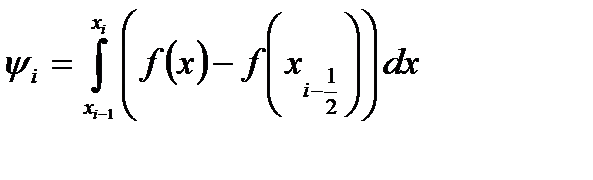
и воспользуемся разложением

Обозначая оценим ψ_i следующим образом:

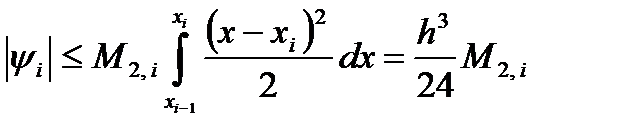
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива формула

т.е. формула имеет погрешность О(h³) при h→0.

Суммируя равенства (26) по I от 1 до N, получим составную формулу прямоугольников

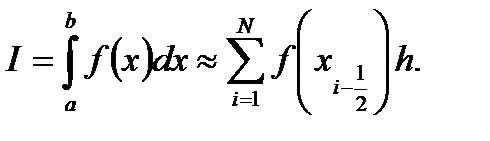
Погрешность этой формулы

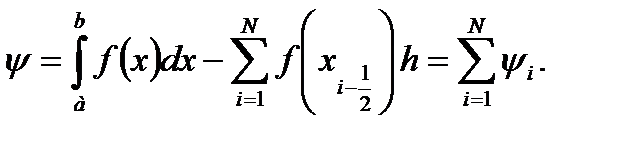
Отсюда, обозначая получим

т.е. погрешность формулы прямоугольников на всем отрезке есть величина О(h²). В этом случае говорят, что квадратурная формула имеет второй порядок точности.

Определение. Приближенное равенство

.

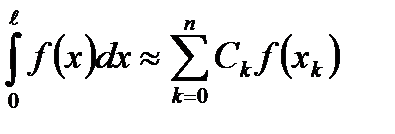Называется квадратурной формулой.

2.2. Формула трапеции. На частичном отрезке (х_i-1, x_i) площадь криволинейной трапеции АВСД заменяется площадью прямоугольной трапеции АВСД (рис. 4).

Рис. 4

Тогда

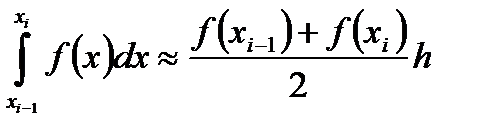
Для оценки погрешности

Представим его в виде

Отсюда получим

Составная формула трапеции имеет вид

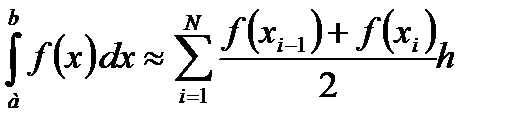
Погрешность этой формулы оценивается следующим образом:

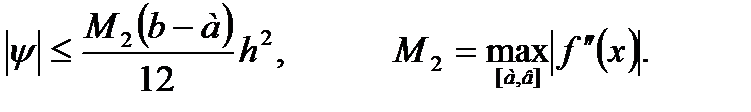
Таким образом, формула трапеции имеет вид, так же как и формула прямоугольников, второй порядок точности, 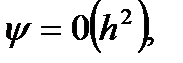но ее погрешность оценивается величиной в два раза большей.

Применение формулы трапеции или прямоугольников требует оценки второй производной 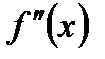на отрезке [а, в]. Если такая оценка затруднительна (или вообще невозможно, например, в случае функции определяемых опытным путем), то в предположений малого изменения (или монотонности) второй производной можно во всех полученных оценках заменить множителя М₂h² наибольшей величиной

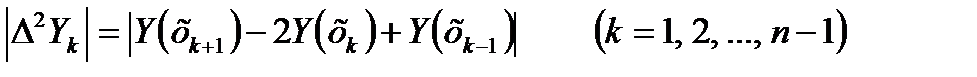
Отсюда видно, что формула прямоугольников и трапеции дает достаточную точность только при достаточно малых разностях второго порядка ∆²У_k (а именно, когда произведения не превосходят допустимой погрешности расчета).

Для уточнения величины интеграла можно использовать, то обстоятельство, что с уменьшением шага h в два раза погрешность формулы трапеций уменьшается примерно в четыре раза. Отсюда следует, что совпадающие знаки в значениях интеграла, вычисленных с шагом h и 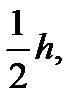можно считать верным. Действительно, если погрешность значения интеграла, вычисленного с шагом обозначить через ε, то погрешность значения интеграла, вычисленного с шагом h, будет приближенно равна 4ε, и значить, разность указанных значений интеграла будет не менее чем 3ε. Поэтому из совпадения m десятичных знаков у рассматриваемых значений интеграла можно заключить, что погрешность 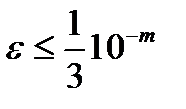, а это означает, что в значений интеграла вычисленном с шагом , все m десятичных знаков верны (здесь предполагается, что погрешность исходных данных пренебрежимо мало).

2.3. Формула Симпсона. При аппроксимации интеграла заменяем функцию f(x) параболой, проходящей через точки (x_I, f(x_I)), I = i-1, i-0,5, i, т.е. представим приближенно f(x) в виде

Тогда

(27)

Вычислим

Из (27) получим, что

Таким образом, приходим к приближенному равенству

которое называется формулой Симпсона.

Погрешность этой формулы ψ_i оценивается так [1]:

На всем отрезке [a, в] формула Симпсона имеет вид

Погрешность этой формулы оценивается неравенством:

Из этой оценки видно, что с уменьшением шага h в два раза погрешность формулы Симпсона уменьшается примерно в 16 раз; поэтому значение интеграла, вычисленное с шагом 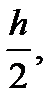содержащий на один верный знак больше, чем значение интеграла, вычисленное с шагом h. Это правило на практике очень удобно при оценке точности интеграла.

Задача 2.1. Между двумя параллельными сбросами и 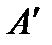находится нефтяная залежь В (рис.5) за пределами которой расположены бесконечно простирающая водоносная область. Стрелками показан приток воды из законтурной области. Ширина залежи в = 1000м, толщина пласта h =15м, проницаемость водоносной области k = 0,2·10^-12м², вязкость законтурной воды Упругоемкости β как нефтяной, так и водоносной частей одинаковы, причем β = 2,5·10^-10 Па^-1, вязкость нефти μ_н = 2мПа·С.

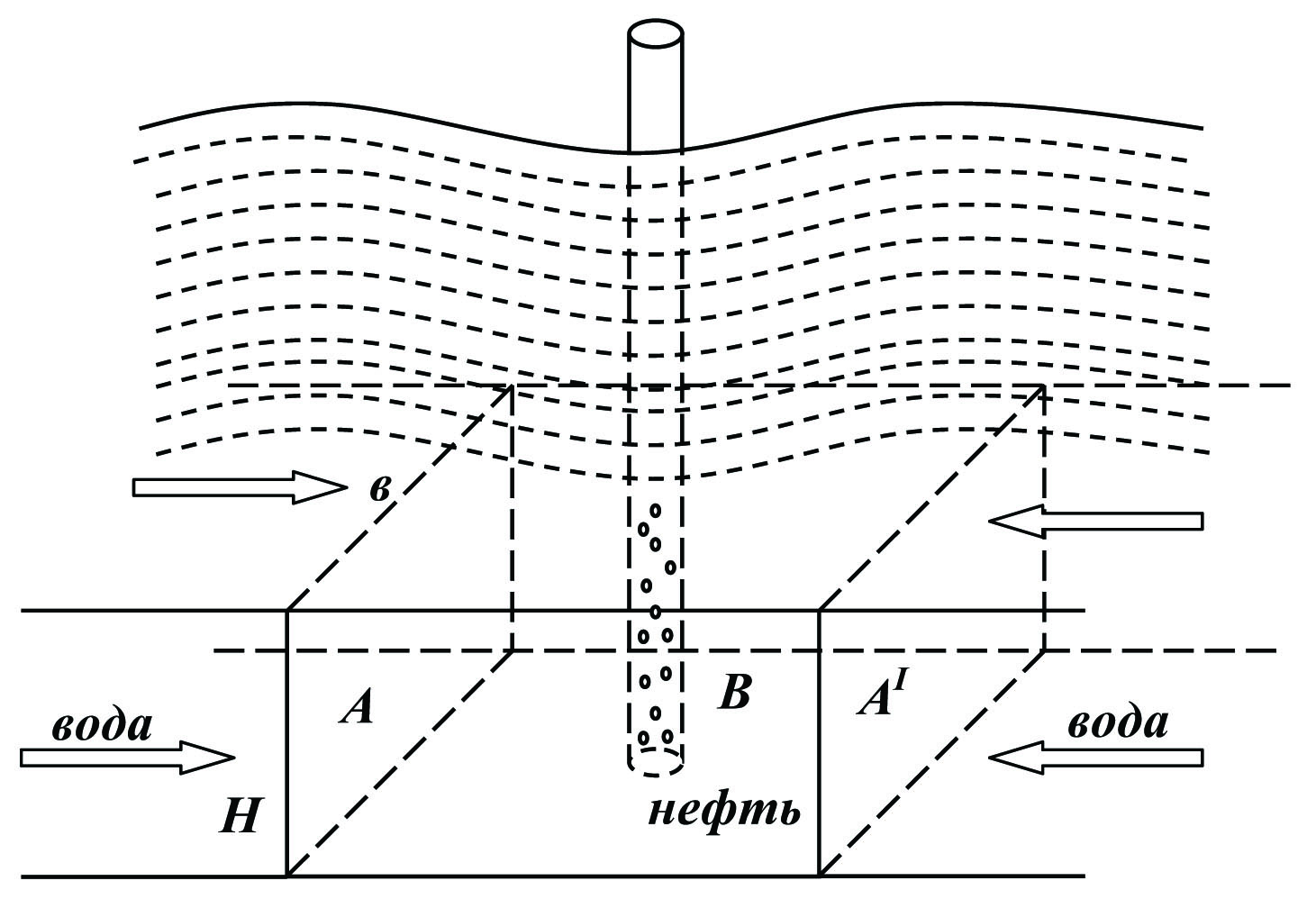
Рис. 5

Отбор жидкости из залежи изменяется во времени следующим образом

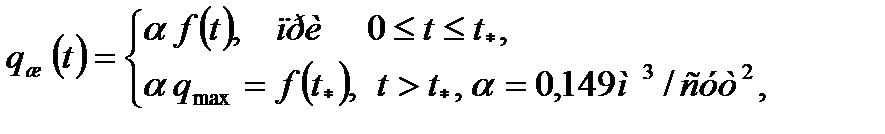
где – время ввода месторождения в разработку. Требуется определить изменение давления на контуре нефтеносности 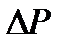, т.е. по сравнению с начальным давлением после начала разработки залежи.

Решение. В начале определим пьезопроводность пласта по формуле

Для расчета изменения во времени давления на контуре нефтяной залежи используя аппроксимацию Карслоу и Егеря [2] имеем:

Данный интеграл вычисления одним из методов: метод прямоугольников, трапеции или Симпсона.