Смешанные двойственные задачи

Этот тип задач появляется тогда, когда модель исходной задачи имеет условия симметричных и несимметричных задач. При составлении смешанной двойственной задачи нужно соблюдать правила симметричных и несимметричных задач.

Теперь сформулируем основные свойства двойственных задач:

1) если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для них выполняется равенство ;

2) если одна из двойственных задач неразрешима, то и другая задача не имеет допустимых решений;

3) если в оптимальном решении одной из двойственных задач какая-либо переменная строго больше нуля, то соответствующее ей ограничение в другой двойственной задаче выполняется как строгое равенство;

4) если при оптимальном решении одной из двойственных задач какое-либо ограничение выполняется как строгое равенство, то соответствующая ему переменная в оптимальном решении другой задачи равна нулю;

5) формулы пересчета решений двойственных задач имеют вид: 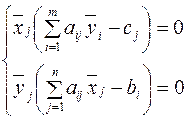, где , ¾ соответствующие оптимальные решения прямой и двойственной задачи.

Пример 2.3. Составить математическую модель двойственных задач, решив одну из них, найти оптимальное решение другой.

Исходная задача: при ограничениях .

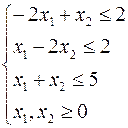Решение. В данном примере имеем симметричную двойственную задачу.

Целевая функция двойственной задачи будет иметь вид . Это выражение получено следующим образом: количество y равно трем, так как в системе ограничений три основных неравенства (неравенства положительности не учитываются); коэффициенты перед y ¾ это свободные коэффициенты неравенств системы ограничений; функция , потому что исходная функция .

Ограничения двойственной задачи имеют вид . Они получены следующим образом:

1) количество основных неравенств равно двум, так как в исходной задаче было две переменных ;

2) коэффициенты первого неравенства ¾ это соответствующие коэффициенты при 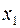в исходной системе ограничений;

3) коэффициенты второго неравенства ¾ это соответствующие коэффициенты при в исходной системе ограничений;

4) свободные коэффициенты ¾ это соответствующие коэффициенты исходной функции ;

5) знаки неравенств изменились на противоположные.

Теперь решим исходную задачу графическим методом и получим оптимальные значения , при которых .

Отсюда на основании теоремы двойственности, получаем, что .

Теперь нужно найти оптимальные значения . Так как , то систему ограничений можно записать в виде равенств .

Подставляем найденные оптимальные значения в систему ограничений исходной задачи , получаем , следовательно .

Тогда система ограничений двойственной задачи примет вид . Решаем ее и получаем оптимальные значения .