Непрерывность функции. Определение непрерывной функции в точке. Односторонняя непрерывность. Кусочно-непрерывные функции, классификация точек разрыва

Ф-ция f(x) называется непрерывной в точке х0, если для любого ε>0 cуществует δ>0, такое,что для всех х ≠ х0 и удовлетворяющих неравенству /x-x0/<δ выполняется неравенство/f(x)-f(x0)/<ε

Другими словами ф-ция непрерывна в точке х0, если существует предел и он равен значению функции в этой точке, то есть lim_x->x0f(x)=f(x0). число А1 называется пределом функции f(x) слева в точке x0, если для любого числа ε>0, существует число b>0, такое что при x принадлежит (х0-δ;х0), выполняется неравенство /f(x)-A1/ε.

Аналогично определяется предел функции справа: lim_x->x0⁺f(x)=A2. Пределы функции слева и справа называются односторонними пределами. Если существует lim_x->x0f(x)=A, то существует и оба односторонних предела, причем А=А1=А2. Если же А1≠А2, то lim_x->x0f(x) не существует и функция не является непрерывной.Точка х0 называется точкой разрыва ф-ции f(x), если f(x) в точке х0 не является непрерывной. Разрывы функций можно классифицировать:

1. Точка х0 называется точкой разрыва, если в этой точке функция f(x) имеет конечные,но не равные друг другу левый и правый пределы, т.е lim_x->x0⁺f(x)=A1, lim_x->x0⁺f(x)=A2, A1≠A2.

2. Точка х0 называется точкой разрыва второго рода, если в этой точке функция f(x) не имеет, по крайней мере, одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.

Алгебраические операции над непрерывными в точке функциями. Непрерывность сложной функции. Существование и непрерывность обратной функции. Свойства непрерывных на отрезке функций (ограниченность, экстремумы и промежуточные значения).

Пусть y=f(x), но x, в свою очередь, является функцией некоторого аргумента t: x=j(t). Тогда комбинация y=f(j(t)) называется сложной функцией, или суперпозицией функции j(t).н-р: а) y=sin(x), x=e^t => y=sin(e^t). Пусть функция j(t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=j(t₀). Тогда функция f(j(t)) непрерывна в точкеt₀. Непрерывность обратной функции

Пусть 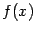-- функция, непрерывная на отрезке 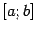. Предположим, что 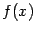монотонна на 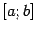; пусть, для

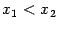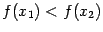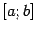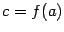определённости, она монотонно возрастает: из следует, что . Тогда образом отрезка будет отрезок , где и 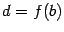(действительно, непрерывная функция принимает любое промежуточное между 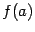и значение, причём ровно один раз, что следует из монотонности). Поэтому существует обратная к 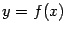функция функция, действующая из в 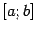. Очевидно, что монотонно возрастает. (Если бы функция 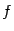была монотонно убывающей, то и обратная к ней функция тоже была бы монотонно убывающей.)

Свойства функций непрерывных на отрезке:

1. Ограниченность функций

А)Функция y=f (x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция f ограничена сверху, если существует такая постоянная М, что для каждого 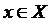выполняется неравенство .

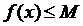Б) Функция y=f (x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждого 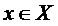выполняется неравенство 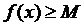. Например, таковыми являются показательные функции, функции y=x²ⁿ, y=Öx.

В) Функция f (x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу. Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x,y=cos x, y=arccos x, y=arcsin x, y=arctg x, y=arcctg x.

При решении уравнений и неравенств свойство ограниченности функций часто играет определяющую роль. Например,

а) если для всех х из некоторого множества Х справедливы неравенства f(x)>M и g(x)<M, где М – некоторое число, то на множестве Х уравнение f(x)=g(x) и неравенство f(x)<g(x) решений не имеют;

б) если для всех х из некоторого множества Х справедливы неравенства f(x) M и g(x)M, где М – некоторое число, то на множестве Х уравнение f(x)=g(x) равносильно системе

2.Экстремум максимальное или минимальное значение функции на заданноммножестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум). Пусть дана функция 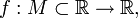и 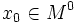— внутренняя точка области определения 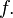Тогда

· называется точкой локального максимума функции если существует проколотая окрестность 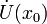такая, что

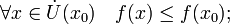
· называется точкой локального минимума функции если существует проколотая окрестность 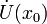такая, что

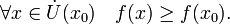
Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.

· называется точкой абсолютного (глобального) максимума, если

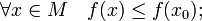
· называется точкой абсолютного минимума, если

Значение функции 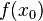называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

3.промежуточные значения.

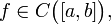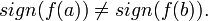· (Теорема о нуле непрерывной функции.) Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой она равна нулю. Формально: пусть и Тогда 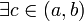такое, что

· В частности любой многочлен нечётной степени имеет по меньшей мере один нуль.

Производная. Определение производной функции в точке. Односторонние производные. Геометрический смысл производной. Производная как чувствительность. Связь между непрерывностью и дифференцируемостью, кусочно-дифференцируемые функции.

Производной от функции y=f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е y’=limΔx->0Δy/Δx=limΔx->0 f(x+Δx)-f(x)/ Δx.

Процесс нахождения производной называется дифференцированием. .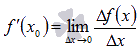

Правой производной 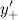функции 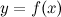в данной точке 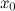называется величина:

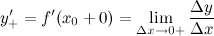
а левой производной - величина:

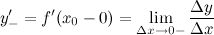
если эти пределы существуют.

Теорема

Для того чтобы в точке существовала производная 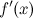, необходимо и достаточно, чтобы в точке функция 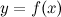имела правую и левую производные, и эти производные были равны между собой: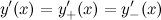

Геометрический смысл производной состоит в том, что численно она равна тангенсу угла между касательной, проведенной к кривой в точке x, и осью абсцисс OX

Связь дифференцируемости с непрерывностью функции в точке.
Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке.
Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции. Обратное утверждение не верно. Например, функция y=|x| непрерывна в точкеx=0, но не дифференцируема в этой точке. Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непр.