 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение устойчивости линейных многомерных систем
|
|
Аналогично одномерным системам рассмотрим качественное поведение многомерных систем, описываемых уравнениями состояния.
ПОСТАНОВКА ЗАДАЧИ
Рассматривается линейная многомерная стационарная система, описываемая уравнением состояния:
х(t) = A x(t) + В g(t), х(0) = х0 (9)
где х - n-мерный вектор состояния; g — r -мерный вектор входных воздействий; t - время; начальный момент времени t0 = 0; х0 - начальное состояние; А, В - матрицы размера (n х n), (n х г) соответственно.
Система называется асимптотически устойчивой, если ее свободное движение xc (t) при g(t) = 0 ограничено при ограниченных начальных состояниях x0 и выполняется условие

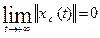 (10)
(10)
КРИТЕРИИ УСТОЙЧИВОСТИ
1. Для асимптотической устойчивости системы (9) необходимо и достаточно, чтобы корни li - характеристического уравнения
det (A - lE) = 0 (11)
имели отрицательные действительные части: Reli < 0, i = 1,..., n, т.е. располагались в левой полуплоскости комплексной плоскости.
2. Для проверки отрицательности действительных частей корней характеристического уравнения (11), можно использовать критерий Рауса-Гурвица.
Необходимое условие устойчивости. Если система (11) асимптотически устойчива, то все коэффициенты характеристического уравнения (11) имеют одинаковые знаки.
Пример 1. Исследовать устойчивость системы, описываемой дифференциальными уравнениями
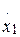 = xl +2х2,
= xl +2х2,
 = 4x1 + 3x2 + g1
= 4x1 + 3x2 + g1
Здесь A = 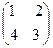 . Характеристическое уравнение
. Характеристическое уравнение 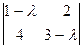 = 0, или
= 0, или
l2 - 4l - 5 = 0
имеет действительные корни разных знаков: l1 =5>0, l2 = -1 < 0. Согласно первому критерию система не является устойчивой.
Пример 2. Исследовать устойчивость системы, описываемой дифференциальными уравнениями
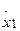 = x2
= x2
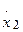 = -xl -2x2 +gl.
= -xl -2x2 +gl.
Здесь А = 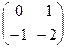 . Характеристическое уравнение
. Характеристическое уравнение 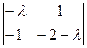 = 0 или
= 0 или
l2 + l +1 = 0
имеет отрицательный корень (кратности 2): l1,2 = - 1. Согласно первому критерию система является устойчивой.
Пример 3. Исследовать устойчивость системы, описываемой дифференциальными уравнениями
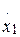 = -x2+g1,
= -x2+g1,
 = x1 + g2.
= x1 + g2.
Перепишем уравнения системы в матричной форме:
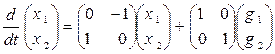
A B
Найдем корни характеристического уравнения. Получим
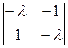 = 0 Þ l2 + 1 = 0
= 0 Þ l2 + 1 = 0
Отсюда l1 =i, l2=-i. Действительная часть корней равна нулю. Согласно первому критерию система не является устойчивой.
Пример 4. При каких положительных значениях параметра а, система, описываемая дифференциальными уравнениями
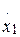 = - axl + g1,
= - axl + g1,
 = (a-2)x3+gl+g2,
= (a-2)x3+gl+g2,
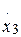 = - x2 – 2a x3 – g2
= - x2 – 2a x3 – g2
будет устойчивой?
Составляем характеристическое уравнение:
det (A - lE) = 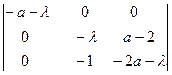 = - (l + а)(l2 + 2аl + а – 2) =
= - (l + а)(l2 + 2аl + а – 2) =
= -l3 – 3аl2 + (- 2а2 – а + 2)l - а2 + 2а = 0.
Его корни: l1 = -а, l2 = - a - 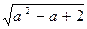 , l3 = - а +
, l3 = - а + 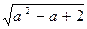 действительные.
действительные.
При а > 0 корни l1 и l2 отрицательны. Из неравенства l3 < 0 находим, что а > 2. Следовательно, рассматриваемая система устойчива при а > 2.
Проверим этот вывод при а = 3, используя критерий Рауса-Гурвица. Характеристическое уравнение имеет вид - l3 - 9l2 -19l - 3 = 0. Умножая его на (-1), получаем коэффициенты: а3=1, а2=9, а1 = 19, а0 = 3. Составляем матрицу: 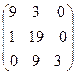 Затем вычисляем ее угловые миноры: ∆1 = 9 > 0, ∆2 = 168 > 0, ∆3 = 504 > 0. Согласно второму критерию система устойчива.
Затем вычисляем ее угловые миноры: ∆1 = 9 > 0, ∆2 = 168 > 0, ∆3 = 504 > 0. Согласно второму критерию система устойчива.
Проверим результат при а = 1. Характеристическое уравнение имеет вид -l3 - 3l2 - l + 1 = 0. Так как коэффициенты этого уравнения имеют разные знаки, то согласно необходимому условию система не является устойчивой.
Отсюда 0 < k < 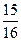 . Кроме того, порядок (m = 0) правой части уравнения меньше порядка (n = 4) левой части. Согласно второму и третьему критериям система устойчива при 0 < k <
. Кроме того, порядок (m = 0) правой части уравнения меньше порядка (n = 4) левой части. Согласно второму и третьему критериям система устойчива при 0 < k < 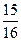 .
.
Варианты заданий
1. Определить устойчивость одномерных систем согласно Вашего варианта с использованием:
а) критерия Рауса-Гурвица. Решите задачу определения устойчивости без использования компьютера;
б) создайте LTI-объект с именем w и определите расположение корней системы, используя команду pzmap (w), сделайте вывод об устойчивости по расположению корней. Определите устойчивость систем с использованием критерия Рауса-Гурвица с использованием компьютера;
в) используя команды step(w) и impulse(w) постройте соответствующие графики и на их основе сделайте выводы об устойчивости систем.
| № варианта | САУ 3-го порядка | САУ 4-го порядка |
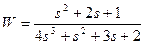
| 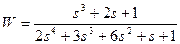
| |
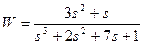
| 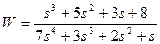
| |
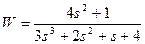
| 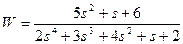
| |
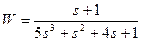
| 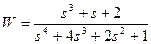
| |
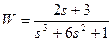
| 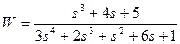
| |
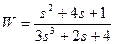
| 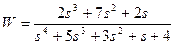
| |
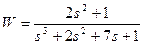
| 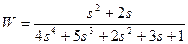
| |
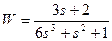
| 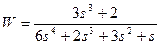
| |
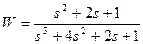
| 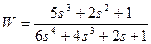
| |

| 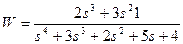
| |
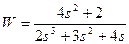
| 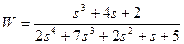
| |
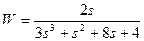
| 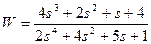
| |
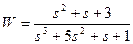
| 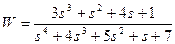
| |
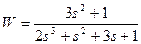
| 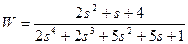
| |
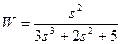
| 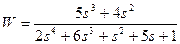
| |
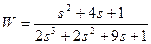
| 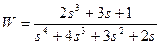
| |
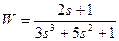
| 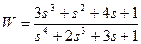
| |
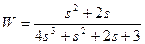
| 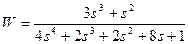
| |
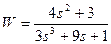
| 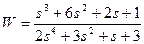
| |

| 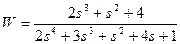
| |
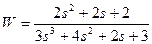
| 
| |
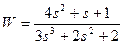
| 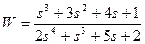
| |
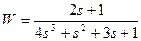
| 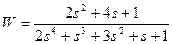
| |
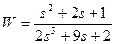
| 
| |
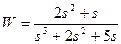
| 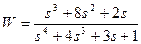
| |
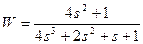
| 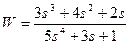
| |
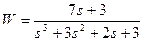
| 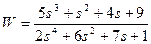
| |
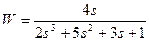
| 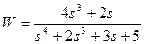
| |
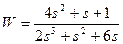
| 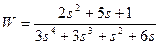
| |
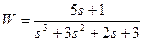
| 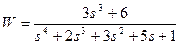
|
2. Исследовать устойчивость многомерных систем, описываемых дифференциальными уравнениями:
1. 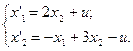 2.
2. 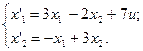 3.
3. 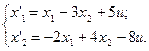
4. 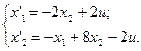 5.
5. 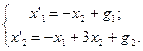 6.
6. 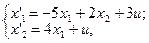
7. 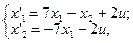 8.
8. 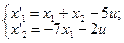 9.
9. 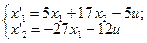
10. 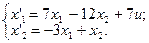 11.
11. 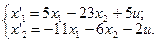 12.
12. 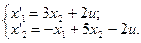
Дата публикования: 2015-10-09; Прочитано: 299 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
