 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Критерий Гурвица
|
|
Стараясь занять наиболее уравновешенную позицию, Гурвиц предположил оценочную функцию, которая находится где-то между точкой зрения крайнего оптимизма и крайнего пессимизма:
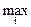 eir = { C
eir = { C 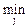 eij + (1- C)
eij + (1- C) 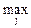 eij },
eij },
где С – весовой множитель.
Правило выбора согласно критерию Гурвица, формируется следующим образом:
матрица решений 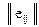 дополняется столбцом, содержащим среднее взвешенное наименьшего и наибольшего результатов для каждой строки. Выбираются только те варианты, в строках которых стоят наибольшие элементы eir этого столбца.
дополняется столбцом, содержащим среднее взвешенное наименьшего и наибольшего результатов для каждой строки. Выбираются только те варианты, в строках которых стоят наибольшие элементы eir этого столбца.
При С =1 критерий Гурвица превращается в ММ-критерий. При С = 0 он превращается в критерий “азартного игрока”
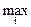 eir =
eir = 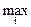
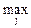 eij,
eij,
т.е. мы становимся на точку зрения азартного игрока, делающего ставку на то, что «выпадет» наивыгоднейший случай.
В технических приложениях сложно выбрать весовой множитель С, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего С:= 1/2.
Критерий Гурвица применяется в случае, когда:
1) о вероятностях появления состояния Fj ничего не известно;
2) с появлением состояния Fj необходимо считаться;
3) реализуется только малое количество решений;
4) допускается некоторый риск.
Сведение матричной игры к задаче линейного программирования
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Итак, пусть дана матричная игра с матрицей А порядка m хn. Согласно свойству 7 оптимальные смешанные стратегии х = (х1,..., хm), y = (y1,..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.
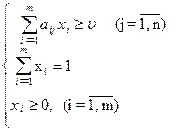
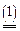
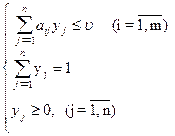
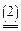
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения:
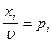
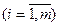 ,
, 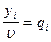
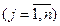 ,
,
Тогда (1) и (2) перепишется в виде:
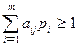 ,
, 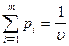 ,
, 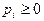 ,
, 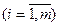 ,
,
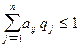 ,
, 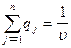 ,
, 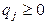 ,
, 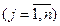 .
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi, чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi 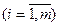 , при которых
, при которых
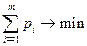 ,
, 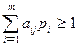 .
. 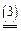
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj,  , при которых
, при которых
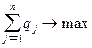 ,
, 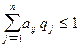 .
. 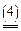
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi  , qj
, qj 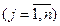 и u. Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
и u. Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
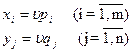
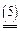
Пример. Найти решение игры, определяемой матрицей.
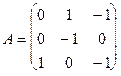
Решение. При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу
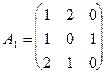
Составим теперь пару взаимно-двойственных задач:
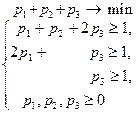
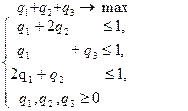
Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
| -1 | -1 | -1 | -3 | ||||||
| q4 | — | ||||||||
| q5 | 
| ||||||||
| q6 | — |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
| -1 | |||||||||
| q4 | 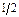
| ||||||||
| q3 | — | ||||||||
| q6 | 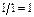
|
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |

| 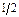
| 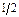
| 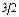
| 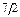
| |||||
| q2 | 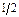
| 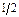
| 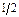
| 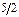
| |||||
| q3 | |||||||||
| q6 | 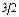
| 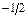
| 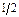
| 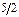
|
Из оптимальной симплекс-таблицы следует, что 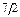
(q1, q2, q3) = (0; 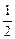 ; 1),
; 1),
а из соотношений двойственности следует, что
(p1, p2, p3) = (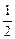 ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
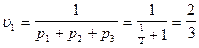 .
. 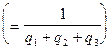 ,
,
а игры с платёжной матрицей А:
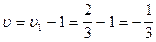 .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = 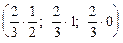 =
= 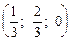
Y = (y1, y2, y3) = (uq1; uq2; uq3) = 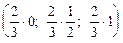 =
= 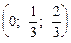 .
.
Дата публикования: 2015-10-09; Прочитано: 380 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
