 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные теоремы о пределах
|
|
Теорема 1. Если существует
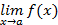
, то он единственный.
Теорема 2.
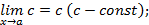
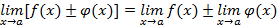
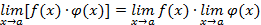
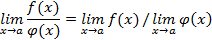
, если
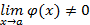
.
Теорема 3. Если функция 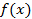 при
при 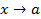 имеет конечный предел
имеет конечный предел 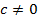 и существует предел функции
и существует предел функции 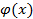 , то
, то
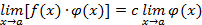
.
Теорема 4. Если в некоторой окрестности точки 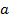
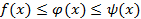 и
и
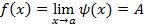
то и
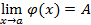
.
Теорема 5. Если при некотором 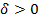 функция
функция 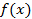 возрастает на
возрастает на 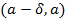 (убывает на
(убывает на 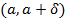 ) и ограничена сверху (снизу), то существует
) и ограничена сверху (снизу), то существует 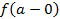 (
( 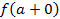 ).
).
Теорема 6. Если для любого 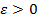 существует
существует 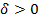 такое, что для произвольных
такое, что для произвольных 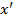 и
и 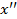 из интервала
из интервала 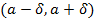 , отличных от
, отличных от 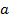 ,
, 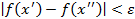 то существует
то существует
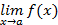
.
Теорема 7. Для существования предела

необходимо и достаточно, чтобы всякой последовательности  , сходящейся к
, сходящейся к 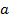 , отвечала последовательность
, отвечала последовательность 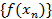 , сходящаяся к
, сходящаяся к 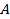 .
.
Теорема 8. Если в некоторой окрестности точки 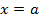 , кроме, может быть, самой этой точки,
, кроме, может быть, самой этой точки, 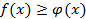 , то и
, то и
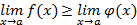
если эти пределы существуют и конечны.
Замечание. Эти теоремы верны и в том случае, когда 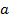 не есть конечное число (иногда с очевидными изменениями формулировок.
не есть конечное число (иногда с очевидными изменениями формулировок.
Пример 17. Вычислить
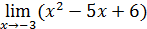
.
Решение. По теореме 2
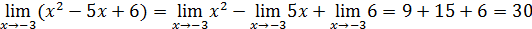
.
Пример 18. Доказать, что последовательность 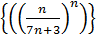 имеет предел, равный нулю.
имеет предел, равный нулю.
Решение. Заметим, что 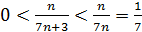 , отсюда
, отсюда
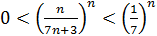 .
.
По теореме 4 о переходе к переделу в неравенствах получаем

а так как 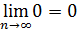 и
и
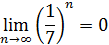
, то
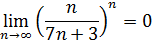
.
Пример 19. Доказать, что
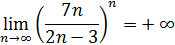
Решение. Заметим, что 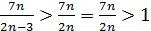 , отсюда
, отсюда 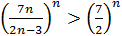 , и по теореме 8 о переходе к пределу в неравенствах
, и по теореме 8 о переходе к пределу в неравенствах
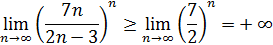
, отсюда
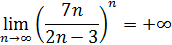
.
Пример 20. Вычислить
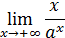
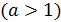 .
.
Решение. Функция, стоящая под знаком предела, по своей конструкции напоминает общий член последовательности из примера 16, и при любом 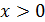 всегда можно указать такое натуральное число
всегда можно указать такое натуральное число 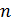 , что
, что 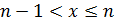 , а следовательно, и
, а следовательно, и  .
.
Теперь, если воспользоваться результатом решения примера 16, то
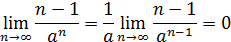
и
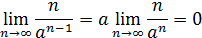
(если

, то  по свойству бесконечно малых и бесконечно больших), а тогда по теореме 4
по свойству бесконечно малых и бесконечно больших), а тогда по теореме 4
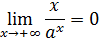
.
Замечание. Более короткий и эффективный способ решения этого примера без использования результата решения примера 16 дает правило Лопиталя (см. §4):

.
1. Исходя из определения предела функции, доказать, что:
1) 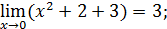 3)
3) 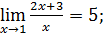 5)
5) 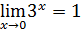 ;
7) ;
7) 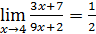 ;
9) ;
9) 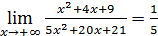 ;
11) ;
11) 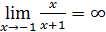 ; ;
| 2) 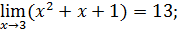 4)
4) 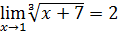 ;
6) ;
6) 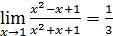 ;
8) ;
8) 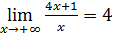 ;
10) ;
10) 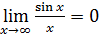 ;
12) ;
12) 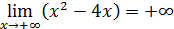 . .
|
2. Исходя из определения предела числовой последовательности, доказать, что:
1) 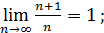 3)
3) 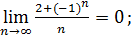 5)
5) 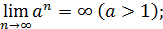 7)
7) 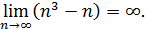
| 2) 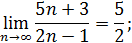 4)
4) 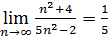 ;
6) ;
6) 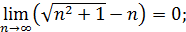
|
3. Используя основные теоремы, вычислить следующие пределы:
1) 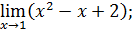 3)
3) 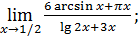 5)
5) 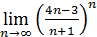 ;
7) ;
7) 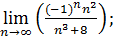
| 2) 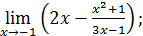 4)
4) 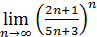 ;
6) ;
6) 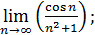
|
4. Вычислить пределы следующих последовательностей, заданных рекуррентными формулами:
1) 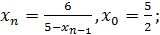 3)
3) 
| 2) 
|
5. Доказать, что следующие переделы не существуют:
Дата публикования: 2015-10-09; Прочитано: 267 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
