 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 4. 3 страница
|
|
:
для x ∈(a– 𝛿, a+ 𝛿) график размещается внутри полосы, ограниченной прямыми y= A± ε.
Следует иметь в виду, что существует бесконечное множество значений 𝛿, отвечающих заданному ε, среди которых есть наибольшее. Однако если речь идет о проверке равенства
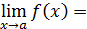
A, то достаточно найти одно значение 𝛿(или доказать его существование), соответствующее произвольному ε>0, заменив неравенство | f (x) –A| < ε более простым, к нему приводящим. При этом часто бывает удобной замена переменной x–a  t.
t.
Пример 1. Доказать, пользуясь определением предела функции, что  . Каким должно быть число 𝛿>0, чтобы для x ∈(– 2 – 𝛿, – 2+𝛿) значения функции 2 x+ 5 отличались от 1 меньше, чем на 0,1; 0,01; 0,001?
. Каким должно быть число 𝛿>0, чтобы для x ∈(– 2 – 𝛿, – 2+𝛿) значения функции 2 x+ 5 отличались от 1 меньше, чем на 0,1; 0,01; 0,001?
Решение: Рассмотрим произвольное число ε >0. Надо убедиться в существовании такого числа 𝛿(ε)>0, чтобы из неравенства | x +2| <𝛿, x≠ – 2, следовало неравенство  , т.е
, т.е 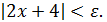 Последнее неравенство равносильно следующему:
Последнее неравенство равносильно следующему:  , так что можно взять 𝛿(ε)= ε/2 или любое положительное число меньше его. Значит,
, так что можно взять 𝛿(ε)= ε/2 или любое положительное число меньше его. Значит,  , ибо для любого числа ε >0 найдено 𝛿= ε/2 такое, что для всех x≠ – 2 и удовлетворяющих неравенству
, ибо для любого числа ε >0 найдено 𝛿= ε/2 такое, что для всех x≠ – 2 и удовлетворяющих неравенству  ,выполняется неравенство
,выполняется неравенство 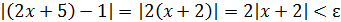 .
.
Полагая в формуле 𝛿(ε)= ε/2 ε=0,1; ε=0,01; ε=0,001, находим 𝛿(0,1)=0,05; 𝛿(0,01)=0,005; 𝛿(0,001)=0,0005.
Пример 2. Доказать, исходя из определения предела функции, что

Решение. Возьмем произвольное число ε >0 и выясним, существует ли такое число 𝛿>0, что из неравенства  , x ≠ 1, следует неравенство
, x ≠ 1, следует неравенство  . Если положить х– 1= t, то доказательство сводится к решению вопроса: найдется ли такое число 𝛿>0, чтобы из неравенства
. Если положить х– 1= t, то доказательство сводится к решению вопроса: найдется ли такое число 𝛿>0, чтобы из неравенства 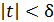 вытекало, что
вытекало, что 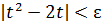 ?
?
С этого момента рассуждения можно вести по-разному. Используя известное неравенство  , получим
, получим 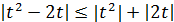 и потребуем, чтобы каждое слагаемое, стоящее в правой части, было меньше ε/2:
и потребуем, чтобы каждое слагаемое, стоящее в правой части, было меньше ε/2: 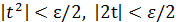 . Полученная система неравенств равносильна следующей:
. Полученная система неравенств равносильна следующей: 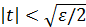 ,
, 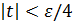 , и за 𝛿 можно взять любое число меньше
, и за 𝛿 можно взять любое число меньше 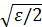 и
и 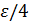 , например
, например 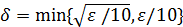 .
.
Или иначе, поскольку  , то при
, то при  ,
, 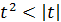 и
и 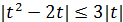 . Отсюда ясно, что если
. Отсюда ясно, что если 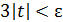 , т.е.
, т.е. 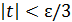 , то тем более
, то тем более 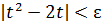 . Последнее неравенство есть результат одновременного выполнения условий
. Последнее неравенство есть результат одновременного выполнения условий  и
и 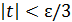 . Поэтому, взяв
. Поэтому, взяв 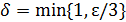 , для
, для 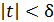 , т.е. для
, т.е. для  , будем иметь одновременно и
, будем иметь одновременно и  , и
, и 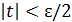 , из чего следует, что
, из чего следует, что 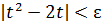 , т.е.
, т.е. 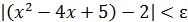 . Значит,
. Значит,

Пример 3. Проверить равенство

Решение. Задавшись некоторым числом ε >0, составим неравенство 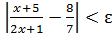 . Элементарными преобразованиями он приводится к равносильному
. Элементарными преобразованиями он приводится к равносильному  . Если неравенство верно, то существует 𝛿>0 такое, что множество значений x, определяемых условием
. Если неравенство верно, то существует 𝛿>0 такое, что множество значений x, определяемых условием  , удовлетворяет этому неравенству. Сделав замену переменной
, удовлетворяет этому неравенству. Сделав замену переменной  , получим два неравенства:
, получим два неравенства:  и
и 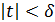 , из которых первое должно быть следствием второго. Пусть
, из которых первое должно быть следствием второго. Пусть  , т.е.
, т.е. 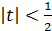 , тогда
, тогда 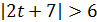 и
и 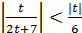 . Поэтому если
. Поэтому если  , то тем более
, то тем более 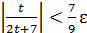 . Приняв
. Приняв 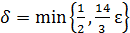 , нетрудно проверить, что для любого ε >0 найдено 𝛿>0 зависящее от ε, а именно
, нетрудно проверить, что для любого ε >0 найдено 𝛿>0 зависящее от ε, а именно 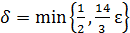 такое, что для любых x≠ 3 из области определения функции, удовлетворяющих неравенству
такое, что для любых x≠ 3 из области определения функции, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  , следовательно,
, следовательно,

Пример 4. Доказать, что
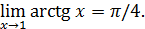
Решение. Возьмем некоторое число ε >0. Чтобы убедиться в справедливости равенства, достаточно найти такое число 𝛿>0, для которого неравенство  приводит к неравенству
приводит к неравенству  < ε. Это неравенство верно при любом х, если
< ε. Это неравенство верно при любом х, если 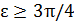 (ибо
(ибо  ). Для таких значений ε в качестве 𝛿 можно взять любое положительное число. Чтобы найти 𝛿 при ε
). Для таких значений ε в качестве 𝛿 можно взять любое положительное число. Чтобы найти 𝛿 при ε 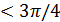 , заметим, что условие
, заметим, что условие  < ε равносильно такому
< ε равносильно такому 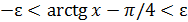 , т.е.
, т.е. 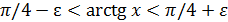 . Если ε
. Если ε  , то
, то 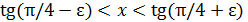 и
и 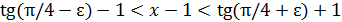 .
.
Если же 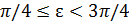 , то двойное неравенство можно заменить одним, а именно неравенством
, то двойное неравенство можно заменить одним, а именно неравенством 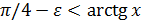 (ибо
(ибо  при всех х) или неравенством
при всех х) или неравенством 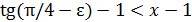 . В этом последнем случае, очевидно, можно взять
. В этом последнем случае, очевидно, можно взять  . При ε
. При ε  из двух чисел
из двух чисел 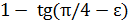 и
и  первое будет меньше (это видно из формул
первое будет меньше (это видно из формул 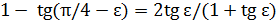 ;
; 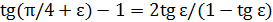 ), так что для 𝛿 можно принять то же выражение. Учитывая, что при
), так что для 𝛿 можно принять то же выражение. Учитывая, что при 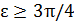 в качестве 𝛿 можно взять любое положительное число, получаем окончательно
в качестве 𝛿 можно взять любое положительное число, получаем окончательно
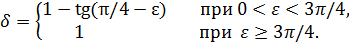
Тогда при таких 𝛿 для любого ε >0 из неравенства  выполняется неравенство
выполняется неравенство  < ε, следовательно,
< ε, следовательно,
2.Односторонние пределы.
Число А называется левосторонним пределом функции f (x), или пределом слева, в точке х=a, если функция f (x) определена в некоторой левосторонней окрестности точки х=a, исключая, может быть, саму эту точку, и если для любого числа ε >0 существует такое число 𝛿(ε)>0, что из неравенства a – 𝛿< x < a следует неравенство | f (x) –A |< ε.
Для предела слева применяются обозначения  , или f (a– 0), так что приведенное определение можно записать, например, в виде равенства
, или f (a– 0), так что приведенное определение можно записать, например, в виде равенства 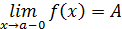 равосторонний предел функции, или предел справа, определяется аналогично и обозначается
равосторонний предел функции, или предел справа, определяется аналогично и обозначается
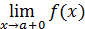
или f (a+ 0).
При a= 0 применяются обозначения 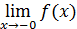 , или f (– 0) для предела слева и
, или f (– 0) для предела слева и 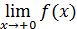 , или f (+ 0) для предела справа.
, или f (+ 0) для предела справа.
Формально понятие предела слева(справа) получается из определения предела функции при условии  и может быть изложено так: равенство
и может быть изложено так: равенство
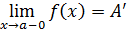
(или f (a– 0) = 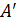 ) означает, что произвольной ε-окрестности точки y=
) означает, что произвольной ε-окрестности точки y= 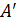 можно поставить в соответствие левостороннюю δ-окрестность точки х=a, для всех точек которой, кроме, может быть, самой точки х=a, значения функции f (x) попадают в ε-окрестность точки
можно поставить в соответствие левостороннюю δ-окрестность точки х=a, для всех точек которой, кроме, может быть, самой точки х=a, значения функции f (x) попадают в ε-окрестность точки 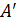 . Аналогичный смысл имеет равенство
. Аналогичный смысл имеет равенство
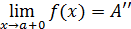
(или f (a+ 0) = 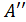 ).
).
Вообще говоря, f (a– 0) ≠ f (a+ 0). Такая ситуация и представлена на рис.2, где (a – δ′, a) есть левосторонняя δ′-окрестность точки х=a, отвечающая ε-окрестности точки y= 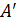 , а (a, a+ δ″) есть правосторонняя δ″-окрестность точки х=a, соответствующая ε-окрестности точки
, а (a, a+ δ″) есть правосторонняя δ″-окрестность точки х=a, соответствующая ε-окрестности точки  .
.
Условие f (a– 0) = f (a+ 0) является необходимым и достаточным условием существования 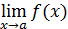 . (Тогда
. (Тогда
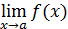
= f (a– 0) = f (a+ 0).)
| Рис.3 |
| Рис.2 |
| a |
| a– δ″ |
| a+ δ″ |
| A′′ |
| A′′ – ε |
| A′′ + ε |
| A + ε |
| A′ |
| A′– ε |
| A′+ ε |
| –b |
| b |
| A |
| A – ε |
| Y |
| Y |
| X |
| X |
 I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AFkjOTrBAAAA3AAAAA8AAABkcnMvZG93bnJldi54bWxET01rg0AQvRf6H5Yp9NasCk3FZpUQEXIL SUrPgztdpe6suFs1/75bCPQ2j/c5u2q1g5hp8r1jBekmAUHcOt2zUfBxbV5yED4gaxwck4IbeajK x4cdFtotfKb5EoyIIewLVNCFMBZS+rYji37jRuLIfbnJYohwMlJPuMRwO8gsSbbSYs+xocORDh21 35cfq2Bv/TZbXjNTfyZv6elwqpsmvyr1/LTu30EEWsO/+O4+6jg/T+HvmXiBLH8BAAD//wMAUEsB Ai0AFAAGAAgAAAAhAASrOV4AAQAA5gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEACMMYpNQAAACTAQAACwAAAAAAAAAAAAAAAAAxAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEgAAAAAAAAAAAAAAAAAuAgAAZHJzL3Bp Y3R1cmV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAFkjOTrBAAAA3AAAAA8AAAAAAAAAAAAAAAAAnwIA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPcAAACNAwAAAAA= ">
I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AFkjOTrBAAAA3AAAAA8AAABkcnMvZG93bnJldi54bWxET01rg0AQvRf6H5Yp9NasCk3FZpUQEXIL SUrPgztdpe6suFs1/75bCPQ2j/c5u2q1g5hp8r1jBekmAUHcOt2zUfBxbV5yED4gaxwck4IbeajK x4cdFtotfKb5EoyIIewLVNCFMBZS+rYji37jRuLIfbnJYohwMlJPuMRwO8gsSbbSYs+xocORDh21 35cfq2Bv/TZbXjNTfyZv6elwqpsmvyr1/LTu30EEWsO/+O4+6jg/T+HvmXiBLH8BAAD//wMAUEsB Ai0AFAAGAAgAAAAhAASrOV4AAQAA5gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEACMMYpNQAAACTAQAACwAAAAAAAAAAAAAAAAAxAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEgAAAAAAAAAAAAAAAAAuAgAAZHJzL3Bp Y3R1cmV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAFkjOTrBAAAA3AAAAA8AAAAAAAAAAAAAAAAAnwIA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPcAAACNAwAAAAA= "> 
Пример 5. Доказать, что

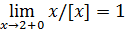
. (Символ [ x ] означает целую часть от числа x, т.е. наибольшее целое число, не превосходящее x.)
Решение. Для x ∈[1,2) [ x ]=1 и x/ [ x ]= x. При произвольном ε >0 неравенство 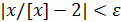 можно записать так:
можно записать так: 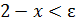 . Следовательно, если принять
. Следовательно, если принять 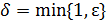 , то из неравенства
, то из неравенства  , с одной стороны, следует, что x ∈(1,2) (ибо 𝛿>0), а с другой стороны
, с одной стороны, следует, что x ∈(1,2) (ибо 𝛿>0), а с другой стороны 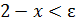 , что формально можно записать и так:
, что формально можно записать и так: 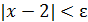 или
или 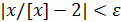 , следовательно,
, следовательно, 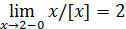 .
.
Чтобы доказать второе равенство, заметим, что для x ∈(2,3) неравенство  переходит в неравенство
переходит в неравенство 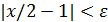 или
или 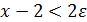 . Поэтому, взяв
. Поэтому, взяв 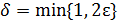 для
для  , т.е. для x ∈(2,3), получим
, т.е. для x ∈(2,3), получим 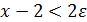 , или
, или 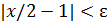 . Поскольку [ x ]=2, то x/ 2 = x/ [ x ], и условие
. Поскольку [ x ]=2, то x/ 2 = x/ [ x ], и условие  есть следствие неравенства
есть следствие неравенства  . Значит,
. Значит, 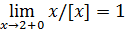 .
.
3.Предел функции в бесконечно удаленной точке.
Понятие предела функции, естественно, обобщается на тот случай, когда a не есть конечное число, если ввести понятие окрестности бесконечно удаленной точки как множества всех значений х, для которых | x | > b, где b> 0 — произвольное число. Тогда равенство 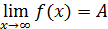 по определению означает, что всякому числу
по определению означает, что всякому числу 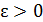 можно поставить в соответствие число b (ε) > 0, такое, что при | x |> b выполняется неравенство | f (x)– A |< ε.
можно поставить в соответствие число b (ε) > 0, такое, что при | x |> b выполняется неравенство | f (x)– A |< ε.
Число b (ε), зависящее от выбранного ε, играет в этом определении ту же роль, что число 𝛿(ε) в определении предела
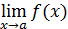
. Каждому значению ε отвечает бесконечное множество значений b, среди которых есть наименьшее, соответствующее наибольшей окрестности бесконечно удаленной точки.
Геометрический смысл записи
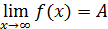
виден на рис.3 произвольной ε-окрестности точки y=A можно сопоставить окрестность бесконечно удаленной точки, т.е. множество x таких, что | x |> b, для всех точек которой A – ε < f (x)< A + ε, т.е. график функции размещается в полосе, ограниченной прямыми у=А± ε.
В частности, если x→+∞ или x→ –∞, определение предела функции выглядит следующим образом:
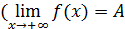
), если для любого положительного числа ε существует число b, такое, что как только x > b, выполняется неравенство | f (x)– A |< ε (рис.4);
число А называется пределом функции f (x) при x→ –∞

), если для любого положительного числа ε существует число b, такое, что как только x < b, выполняется неравенство | f (x)– A |< ε (рис.5).
Понятия, определяемые равенствами
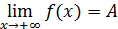
,
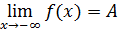
обобщают понятия односторонних пределов функции. Рис.4 и 5 дают их геометрическую интерпретацию.
Пример 6. Доказать, что
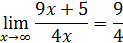
. Каким должно быть число b, чтобы для | x| > b значения функции отличались от 9/4 меньше, чем на 0,1; 0,002; 0,000005?
Решение. Пусть ε >0 — произвольное число. Доказываемое утверждение верно, если существует b> 0 такое, что при | x| > b выполняется неравенство | f (x)–9/4|< ε, т.е.  , или
, или 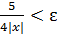 . Последнее неравенство равносильно следующему: | x| > 5/(4ε), так что положив b= 5/(4ε), при | x| > b получим как следствие
. Последнее неравенство равносильно следующему: | x| > 5/(4ε), так что положив b= 5/(4ε), при | x| > b получим как следствие 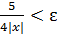 , или
, или  . Следовательно,
. Следовательно, 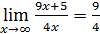 .
.
На остальные вопросы получаем ответ простым вычислением значений b (ε) = = 5/(4ε) при ε, равном 0,1, 0,002 и 0,000005, который можно оформить так:
| ε | 0,1 | 0,002 | 0,000005 |
| b | 12,5 |
Пример 7. Доказать, что 
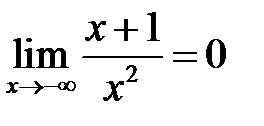
Решение. Исходя из определения предела функции, для любого ε >0 надо найти такое b, что для всех x<b выполняется неравенство  ε.
ε.
Преобразуем последнее неравенство:
 и потребуем, чтобы каждое из слагаемых было меньше ε/2, тогда их сумма будет меньше ε: 1/| x|< ε/2, 1/ x2< ε/2, или | x|> 2/ ε, | x|>
и потребуем, чтобы каждое из слагаемых было меньше ε/2, тогда их сумма будет меньше ε: 1/| x|< ε/2, 1/ x2< ε/2, или | x|> 2/ ε, | x|> 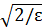 .
.
Так как x→ – ∞, то можно считать x< 0 и тогда | x|= –x, и система неравенств будет равносильной следующей: –x >2/ε, –x> 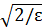 или x < – 2/ε, x<–
или x < – 2/ε, x<– 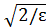 . Вместо b можно взять, например, min{ –
. Вместо b можно взять, например, min{ –  , –
, – 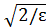 }. Итак, для всех x < min{ –
}. Итак, для всех x < min{ –  , –
, – 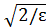 } при любом ε >0 выполняется неравенство
} при любом ε >0 выполняется неравенство  ε, следовательно,
ε, следовательно,  .
.
Дата публикования: 2015-10-09; Прочитано: 407 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
