Численные методы решения задач нестационарной теплопроводности

Температурное поле в стенке при ее нагревании можно определить экспериментально, однако это не всегда возможно из-за того, что необходимо создавать специальные экспериментальные установки и оснащать их измерительным оборудованием.

На сегодня существует много численных методов приближенного решения задач нестационарной теплопроводности, которые разрешают получить результаты, удовлетворительно согласующиеся с результатами экспериментов. Широкое распространение имеет приближенный метод расчета температурного поля – метод конечных разностей. Его основная идея состоит в том, что решение непрерывной задачи, которое связывает между собою температуру тела в бесконечном множестве точек в любой момент времени, можно заменить на нахождение температуры в конечном числе точек пространства в конечное число моментов времени, то есть бесконечно малые разности dx и d t между пространственными и временными координатами соседних точек заменяются на конечные разности D x и Dt соответственно. Тогда в одномерном случае мы имеем дело не с полем температур t (x, t), а с конечным количеством значений температуры.

Рассмотрим реализацию метода сеток на примере одномерной задачи о нагревании плоской стенки толщиной d на протяжении времени Γ при граничных условиях третьего и первого рода. Исходная задача состоит в отыскании функции t(x, t ), что удовлетворяет в области определения 0< x < d и 0 < t < Г уравнению

, (2.82)

с начальным условием

t (x, 0) = t ₀(х), (2.83)

(где t ₀(х) – заданное начальное распределение температуры), и с граничными условиями 3-го рода (при х = 0) и 1-го рода (при х = d)

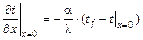; t (d, t) = t_w (t), (2.84)

где t_f (t), a и l – заданные температура среды, коэффициенты теплоотдачи и теплопроводности со стороны поверхности с х = 0, t_w (t) – заданная температура на поверхности с х = d.

Разобьем стенку на целое количество слоев шириной D х, а время на целое количество интервалов 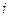продолжительностью Dt. Пронумеруем точки деления оси x целым параметром i =0, 1, 2,..., n-1, n. Координаты этих точек определяются по формуле x_i º i× D х. Аналогично пронумеруем точки деления временного интервала целым параметром k = 0, 1, 2, …, m– 1, m. Моменты времени, которые отвечают этим точкам, вычисляются по формуле t_k = k× Dt. Отметим, что ширина интервалов и количество участков разбивки связанные соотношениями:

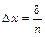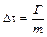; ,. (2.85)

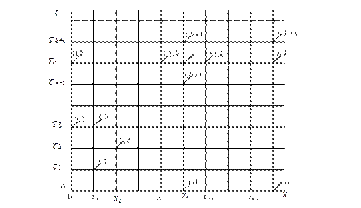
Таким образом, мы заменили непрерывный прямоугольник области определения поля температур сеткой точек (смотри рисунок 2.15).

Будем, прежде всего, интересоваться не всем полем температур (x, t ), а конечным множеством значений температуры в узлах сетки. Для сокращения записей введем отдельные пометки для значений температур в точках сетки:

t_i,k º t (x_i , t _k ), (2.86)

температура в точке x_i, в момент времени t _k.

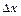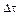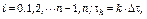Рисунок 2.15 – Пространственно-временная сетка с шагами в направлении оси х и в направлении оси времени ( где где )

Для определения множества сеточных значений температуры надо выяснить, какому уравнению они удовлетворяют. Понятно, что это должен быть какой-либо дискретный аналог нестационарного уравнения теплопроводности (2.82). Получим его. Первую частную производную от температуры по времени можно представить в виде конечных разностей

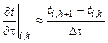, (2.87)

где пара индексов i,k означают, что соответствующая величина берется при x = x_i и t = t _k.

Первая частная производная от температуры по пространственной координате выражается аналогично

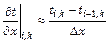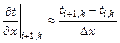; , (2.88)

Вторая производная по определению является первой производной от первой производной. В соответствии с этим ее запись в конечных разностях имеет вид:

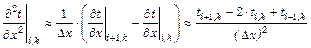, (2.89)

Подставляя полученные формулы (2.88), (2.89), в уравнение нестационарной теплопроводности (2.82), получим алгебраическое уравнение

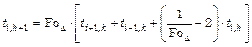, (2.90)

в котором в качестве параметра выступает критерий Фурье

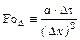. (2.91)

Оно называется сеточным уравнением или разностной схемой. Эта так называемая явная разностная схема. С ее помощью можно относительно просто вычислить значения температуры t_i,k+1 во всех точках x_i (i = 1, 2, 3,..., n -1) для момента времени t _{k +1} = (k +1)×Dt, если известные значения температур t_i,k во всех точках x_i (i = 0, 1, 2, 3,..., n) в момент времени t _k = k× Dt, который предшествует данному. Таким образом, задав значение температуры t_{i ,0} во всех точках x_i в начальный момент времени t₀ = 0, можно, последовательно используя формулу (2.90), рассчитывать температуры t_i,k во все следующие моменты: сначала t_i,1, дальше t_{i ,2}, дальше t_{i ,3} и так далее.

Исследования показывают, что рассмотренная вычислительная схема устойчивая, то есть точность расчетов поля температуры повышается с уменьшением величин D х и Dt, если выполняется условие

.

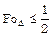Уравнение (2.90) значительно упрощается, если использовать шаги D х и Dt, для которых выполняется соотношение

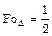, (2.92)

В этом случае разностная схема принимает вид

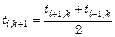. (2.93)

На последней формуле базируется графический метод решения задач теплопроводности, который довольно часто используется в инженерной практике.

t_{n,k× Dt} = t (n^. D x, k ^. Dt),

в точках с координатами x = n× D x:

t = k ^. Dt,

где n и k – целые числа.

Рисунок 2.16 это иллюстрирует.

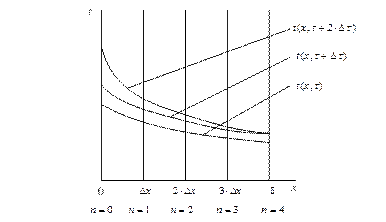
Рисунок 2.16 – Графики зависимости температуры точек плиты от

координаты x.

На нем приведены графики зависимости температуры точек плиты от координаты x (расстояния от горячей поверхности) для трех моментов времени: t, t + Dt и t + 2Dt, то есть графики функций t (x, t), t (x, t+Dt) и t (x, t+2×Dt).

В данном случае плиту, которая имеет толщину d, разбивают на четыре пласта толщиной D x. Температура определяется при x= n^. D x. Значениям n = 0 и n = 4 отвечают поверхности плиты, а значениям n = 1, 2, 3 – внутренние границы слоев. (Соответствующие точки приведены на графиках).

Уравнение (2.93) позволяет, зная все температуры (то есть при n = 0, 1, 2, 3, 4 на рисунке 2.16) в момент времени t, рассчитать температуры во внутренних точках плиты (при n = 1, 2, 3 на рисунке 2.16) в следующий момент – через интервал времени Dt. Оно выполняется при соблюдении условия:

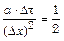. (2.94)

Содержание последней проясняется, если вспомнить, что параметр Фурье:

,

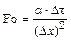это приведенное время распространения изменений температуры на расстоянии D x.

Связь температур на поверхностях плиты (n = 0, 4, рисунок 2.16) с другими температурами зависит от граничных условий.

В случае граничных условий первого рода температура на границе задается непосредственно. В случае граничных условий третьего рода эта температура ищется из приближенного равенства тепловых потоков по разные стороны поверхности раздела сред. В плите этот поток определяется по закону Фурье, а извне – по закону Ньютона–Рихмана.

Как результат температура на поверхности плиты t_w рассчитывается в соответствии с соотношением:

, (2.95)

где a – коэффициент теплоотдачи от среды к поверхности теплообмена, температура которой определяется, Вт/(м^2.К);

t_f – температура внешней среды, которая контактирует с данной поверхностью, ^оС;

t – температура плиты в плоскости соответствующих слоев (n = 1, или n = 3 – рисунок 2.16), ºС.