Центральная предельная теорема

Хорошо известно, что большинство встречающихся в природе случайных величин имеют распределение, по крайней мере очень близкое к нормальному. Теоретическое объяснение этому факту дает центральная предельная теорема Ляпунова.

Рассмотрим, как и в предыдущем случае, сумму независимых случайных величин 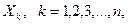, но не усредненную по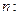

,

а нормированную:

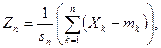
где

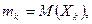
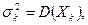
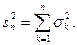
Правила нахождения математического ожидания и дисперсии суммы независимых случайных величин позволяют утверждать, что 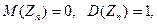а случайные величины с такими свойствами называются нормированными.

Определение 1. Будем говорить, что последовательность независимых случайных величин 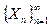удовлетворяет условию Ляпунова, если

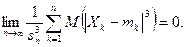
Поясним смысл условия Ляпунова. Для произвольного 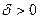рассмотрим случайные события

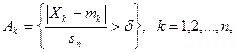
которые заключаются в том, что слагаемые нормированной суммы 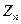по абсолютной величине превосходят 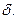Нетрудно видеть, что

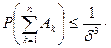
(2)

По условию Ляпунова выражение справа в (2) стремиться к нулю. Таким образом, все слагаемые нормированной суммы 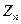равномерно малы в том смысле, что вероятность хотя бы одного из них превзойти по абсолютной величине 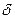стремится к нулю при возрастании числа слагаемых.

Условие Ляпунова будет выполнено, если независимые случайные величины

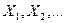имеют одно и тоже математическое ожидание, дисперсию и абсолютный центральный момент третьего порядка:

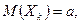
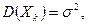
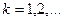
Действительно, в этом случае

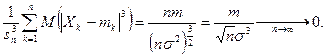
В частности, условие Ляпунова будет выполнено, если независимые случайные величины 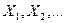имеют одно и тоже распределение.

Теорема 1(Центральная предельная или теорема Ляпунова). Пусть 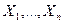- независимые случайные величины, имеющие какие угодно распределения, удовлетворяющие условию Ляпунова. Тогда функция распределения 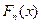случайной величины 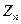при 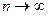поточечно сходится к функции распределения 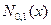случайной величины, распределенной по нормальному стандартному закону.

Центральной предельной теоремой пользуются для приближенного вычисления вероятностей, связанных с суммами большого числа независимых и одинаково распределенных случайных величин. При этом распределение нормированной суммы заменяют на стандартное нормальное распределение, а за распределение суммы 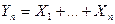берут нормальный закон распределения с параметрам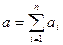и и Этим объясняется тот факт, что вся классическая математическая статистика строится только для нормально распределенных случайных величин, и при этом считается применимой всегда. Но насколько велика ошибка замены распределения случайной величины 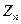на стандартное нормальное распределение? Следующая теорема позволяет оценить погрешность такой замены.

Теорема 2(Неравенство Бери-Эссеена).

Пусть независимые случайные величины 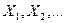имеют одно и тоже математическое ожидание, дисперсию и абсолютный центральный момент третьего порядка:

,

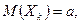
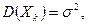
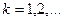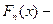функция распределения нормированной суммы 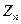. Тогда 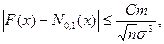где

Пример 1. В кассе учреждения имеется сумма 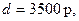в очереди стоит 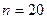человек, сумма 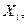которую нужно выплатить отдельному человеку, является случайной величиной, со средним значением 150 р. и 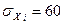р. Найти:

1. Вероятность того, что суммы 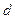не хватит для выплаты всем людям в очереди.

2. Какую сумму 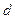надо иметь в кассе, чтобы с вероятностью 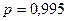ее хватило для всей очереди.

Решение. При 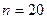уже можно считать, что случайная величина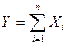

имеет нормальный закон распределения с параметрами

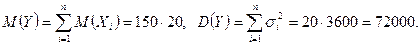
Тогда:

1.

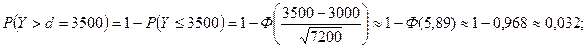
2. 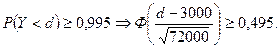По таблицам находим, что для этого должно выполняться неравенство , откуда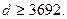

Рекомендуемая литература

1. Н.Ш. Кремер. Теория вероятностей и математическая

статистика. М.: ЮНИТИ-ДАНА, 2004.

2. В.Е. Гмурман. Теория вероятностей и математическая статистика. М.: Высшая школа, 2004.