Закон больших чисел

Лекция 8. Раздел 1. Теория вероятностей

Рассматриваемые вопросы

1) Закон больших чисел.

2) Центральная предельная теорема.

Закон больших чисел.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых при тех или иных условиях устанавливается возможность приближения средних характеристик большого числа испытаний

к некоторым определенным постоянным. При доказательстве теорем такого рода используются неравенства Маркова и Чебышева, представляющие также самостоятельный интерес.

Теорема 1(неравенство Маркова). Если случайная величина 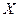принимает неотрицательные значения и имеет математическое ожидание, то для любого положительного числа 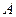справедливо неравенство

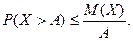
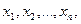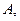Доказательство проведем для дискретной случайной величины. Будем считать, что она принимает значений из которых первые меньше или равны а все остальные- больше Тогда

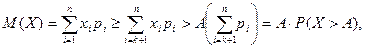
откуда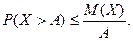

Пример 1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течении следующего часа число вызовов на коммутатор:

1) превысит 400;

2) будет не более 500.

Решение. 1) Пусть случайная величина 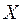есть число звонков, поступающих на коммутатор в течение часа. Среднее значение-это 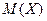. Значит 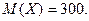Нам надо оценить . Согласно неравенству Маркова

2) 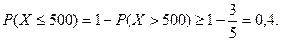Таким образом, вероятность того, что число вызовов будет не более 500, не менее 0,4.

Пример 2. Сумма всех вкладов в отделение банка составляет 2 млн. рублей, а вероятность того, что случайно взятый вклад не превышает 10 тыс. рублей, равна 0,6. Что можно сказать о числе вкладчиков?

Решение. Пусть случайно взятая величина 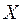есть размер случайно взятого вклада, а 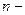число всех вкладов. Тогда 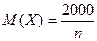(тыс.). Согласно неравенству Маркова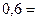 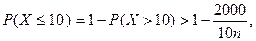откуда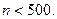

Пример 3. Пусть 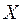-время опоздания студента на лекцию, причем известно, что в среднем он опаздывает на 1 минуту. Оцените вероятность того, что студент опоздает не менее чем на 5 минут.

Решение. По условию 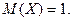Применяя неравенство Маркова, получаем, что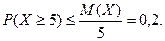

Таким образом, из каждых 5 студентов опоздает по крайней мере на 5 минут не более, чем 1 студент.

Теорема 2 (Неравенство Чебышева). .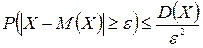

Доказательство. Пусть случайная величина Х задается рядом распределения

			…
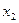
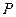
	р1	р2	…	рп

Согласно определению дисперсии 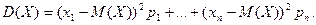Исключим из этой суммы те слагаемые, для которых 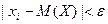. При этом, т.к. все слагаемые, неотрицательны, сумма может только уменьшится. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

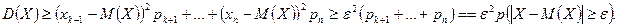
Следовательно, .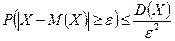

Неравенство Чебышева позволяет оценивать сверху вероятность отклонения случайной величины от ее математического ожидания на основе информации лишь о ее дисперсии. Оно широко используется, например, в теории оценивания.

Пример 4. Монета подбрасывается 10 000 раз. Оценить вероятность того, что частота выпадения герба отличается от на 0,01 или более.

Решение. Введем независимые случайные величины , где – случайная величина с рядом распределения

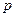
Тогда так как 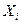распределена по биномиальному закону с 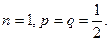Частота появления герба есть случайная величина 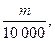где 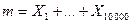. Поэтому дисперсия частоты появления герба есть 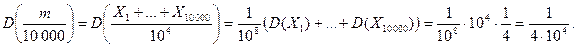Согласно неравенству Чебышева, .

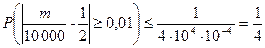Таким образом, в среднем не более чем в четверти случаев при 10 000 подбрасываниях монеты частота выпадения герба будет отличаться от на одну сотую или больше.

Теорема 3 (Чебышева). Если 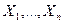– независимые случайные величины, дисперсии которых равномерно ограничены (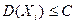), то

.

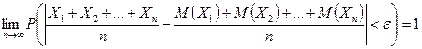Доказательство. Так как

,

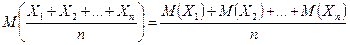то применяя неравенство Чебышева, получаем

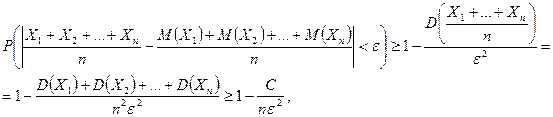
откуда

.

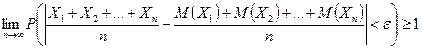Поскольку вероятность события не может быть больше 1, получаем требуемое.

Следствие 1. Если 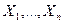– независимые случайные величины с равномерно ограниченными дисперсиями и одним и тем же математическим ожиданием, равным а, то

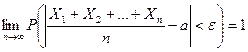. (1)

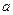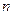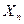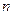Равенство (1) говорит о том, что случайные отклонения отдельных независимых случайных величин от их общего среднего значения при большом в своей массе взаимно погашаются. Поэтому, хотя сами величины случайны, их среднее при большом практически уже не случайно и близко к 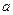. Это означает, что если 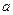заранее неизвестно, то его можно вычислить с помощью среднего арифметического 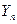. Это свойство последовательностей независимых случайных величин называется законом статистической устойчивости. Закон статистической устойчивости обосновывает возможность применения анализа статистик при принятии конкретных управленческих решений.

Теорема 4 (Бернулли). Если в каждом из п независимых опытов вероятность р появления события А постоянна, то

,

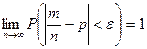где 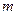– число появлений события А при этих п испытаниях.

Доказательство. Введем независимые случайные величины 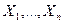, где Х _i – случайная величина с рядом распределения

Х i
р i	q=1–p	p

Тогда М(Х _i)=р, D(Х _i)=рq. Так как 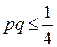, то D(Х _i) ограничены в совокупности. Из теоремы Чебышева следует, что

.

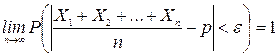Но Х₁+Х₂+…+Х _п есть число 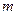появлений события А в серии из п испытаний.

Смысл теоремы Бернулли заключается в том, что при неограниченном увеличении числа одинаковых независимых опытов с практической достоверностью можно утверждать, что частота появления события будет сколь угодно мало отличаться от вероятности его появления в отдельном опыте (статистическая устойчивость вероятности события). Поэтому теорема Бернулли служит переходным мостиком от теории приложений к ее применениям.