 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формула интегрирования по частям
|
|
Теорема 1. Пусть функции 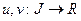 дифференцируемы на
дифференцируемы на 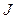 , и функция
, и функция 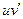 имеет примитивную на
имеет примитивную на 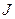 . Тогда функция
. Тогда функция  также имеет примитивную на
также имеет примитивную на 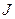 и справедливо равенство
и справедливо равенство
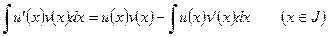 . (1)
. (1)
Коротко (1) записывается так:
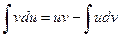 (1′)
(1′)
При этом точный смысл (1) заключается в следующем: если  − примитивная для
− примитивная для  , то
, то
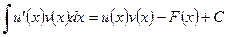 .
.
Пример 1. Найти 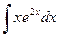 .
.
Решение. Положим 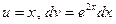 . Тогда
. Тогда 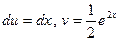 (в качестве
(в качестве 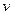 мы берём наиболее простую функцию, для которой
мы берём наиболее простую функцию, для которой 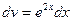 , т. е. не включаем в состав
, т. е. не включаем в состав 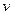 произвольную постоянную), и
произвольную постоянную), и 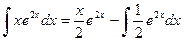 . Мы свели решение примера к вычислению такого интеграла, где первообразная очевидна:
. Мы свели решение примера к вычислению такого интеграла, где первообразная очевидна: 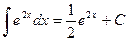 . Следовательно,
. Следовательно,
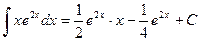 .
.
Пример 2. Найти 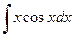 .
.
Решение. 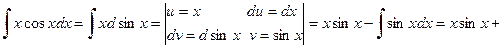
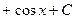 .
.
Пример 3. Найти 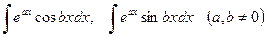 .
.
Решение. Пусть 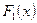 – примитивная функции
– примитивная функции 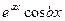 ,
, 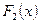 – примитивная функции
– примитивная функции  . Тогда имеем
. Тогда имеем
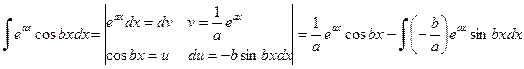 ,
,

Следовательно, найдутся постоянные  и
и 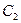 такие, что
такие, что
 , (2)
, (2)
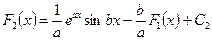 . (3)
. (3)
Подставляя (3) в (2), получаем
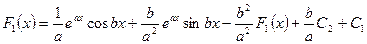 ,
,
откуда
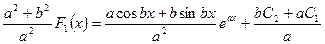 ,
,
или
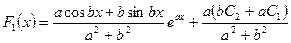 .
.
Значит,  также есть первообразная функции
также есть первообразная функции 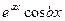 , поэтому
, поэтому
 . (4)
. (4)
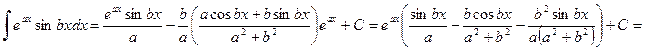
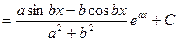 . (5)
. (5)
Пример 4. Найти 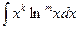 , где
, где 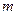 - натуральное число.
- натуральное число.
Решение. 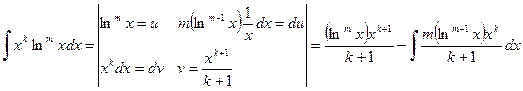 .
.
Пример 5. Найти 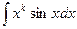 , где
, где 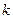 - натуральное число.
- натуральное число.
Решение. 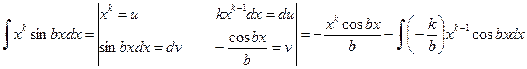 .
.
Пример 6. Найти 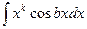 , где
, где 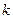 - натуральное число.
- натуральное число.
Решение. 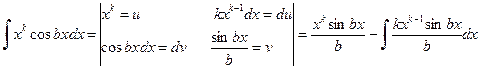 .
.
Пример 7. Найти 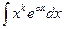 , где
, где 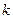 - натуральное число.
- натуральное число.
Решение. 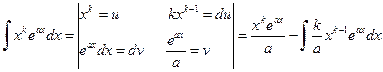 .
.
Примеры 4-7 показывают, что эти интегралы можно найти повторным применением формулы интегрирования по частям. Однако всегда при повторном применении этой формулы нужно следить, чтобы мы не проделали в обратном порядке те выкладки, которые встретились на первом шаге. В противном случае мы придём к ничего не дающему тождеству:
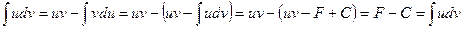 ,
,
где  −примитивная для
−примитивная для 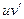 .
.
Дата публикования: 2015-09-18; Прочитано: 184 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
