Частные производные высших порядков

Пусть 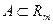- открытое множество, . Предположим, что на множестве 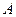(т.е. в каждой точке множества 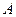) существует частная производная 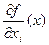. Может оказаться, что функция 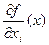в точке имеет частную производную по переменной 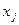. Тогда эта производная называется частной производной второго порядка функции в точке и обозначается одним из символов 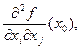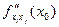. При выполнении соответствующих условий аналогично определяются частные производные порядка 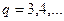. Частная производная, взятая сначала по 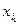, затем по 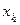и т.д. обозначается 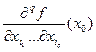. Если среди индексов 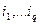имеются различные, то частная производная называется смешанной. Если , первые 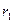индексов 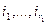совпадают с 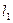, последующие индексов совпадают с 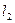и т.д., то 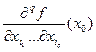обозначают .

Пример 1. Пусть 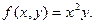Тогда:

В рассмотренном примере смешанные производные 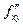и 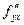, разнящиеся последовательностью дифференцирований, совпадают. Покажем на примере, что подобное совпадение не всегда имеет место.

Пример 2. Пусть

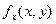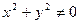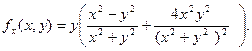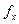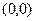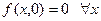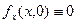Найдем . Если , то Для нахождения производной в точке надо, согласно определению, продифференцировать функцию по и затем положить равным нулю. Так как , то , и тем самым 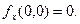Для определения 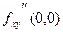мы должны продифференцировать по 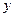функцию 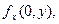а затем положить 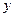равным нулю. Имеем

Таким образом, 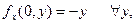откуда 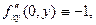и тем самым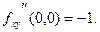

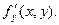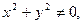Теперь найдем Если то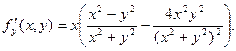

Для нахождения производной в точке 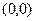надо, согласно определению, продифференцировать функцию 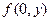по 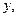а затем положить 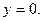Так как

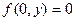
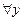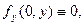, то и тем самым 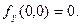Для определения 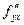в точке 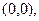мы должны продифференцировать функцию 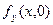по 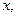а затем

положить Имеем

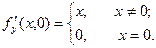
Таким образом, 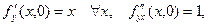и тем самым 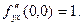Значит

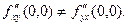
Возникает вопрос: каковы достаточные условия, при которых значения смешанных производных не зависят от последовательности дифференцирования?

Теорема 1. Пусть 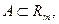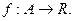Допустим, что функция имеет на 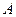всевозможные частные производные до порядка 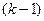включительно и смешанные производные -го порядка, причем все эти производные непрерывны. Тогда значение любой -той смешанной производной не зависит от порядка, в котором производятся последовательные дифференцирования.