 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторно-координационный способ нахождения угла прямой с плоскостью
|
|
Если прямая AB пересекает плоскость t и не перпендикулярна 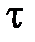 , то углом между прямой AB и плоскостью t называется угол между прямой AB и ее проекцией на плоскость t.
, то углом между прямой AB и плоскостью t называется угол между прямой AB и ее проекцией на плоскость t.
Решение такого рода задач по нахождению угла прямой с плоскостью состоит в следующем: используя особенности заданной фигуры, вводят в пространстве прямоугольную систему координат, находят координаты нужных точек, координаты какого-нибудь вектора 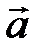 , коллинеарного прямой AB, и вектора
, коллинеарного прямой AB, и вектора 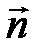 – нормального вектора плоскости t. Далее находят косинус угла между векторами
– нормального вектора плоскости t. Далее находят косинус угла между векторами 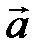 и
и 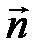 .
.
Так как y - это угол между двумя прямыми, то 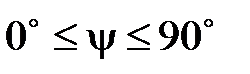 . Но угол между векторами может принимать значения от 0 ° до 180 °.
. Но угол между векторами может принимать значения от 0 ° до 180 °.
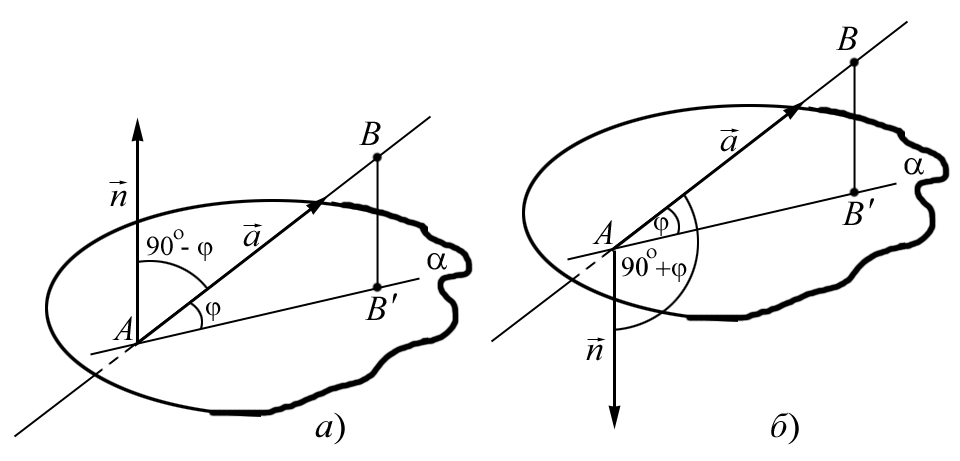
| Рис. 3.7 |
1. Если угол между векторами
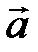 и
и 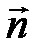 изменяется от
изменяется от 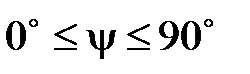
(рис. 3.7, а), то cos
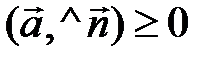 и
и 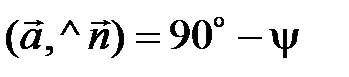 . Но
. Но 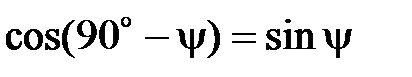 , то есть в этом случае
, то есть в этом случае
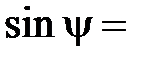 сos
сos 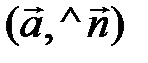 . (3.20)
. (3.20)
2. Если угол между векторами 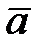 и
и 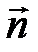 изменяется от
изменяется от 
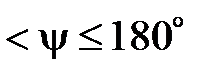
(рис. 3.7, б), то cos 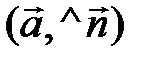
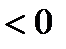 и
и 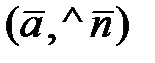 = 90 ° + y. Но
= 90 ° + y. Но 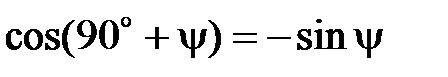 , т. е. в этом случае
, т. е. в этом случае
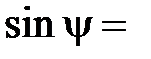 – сos
– сos 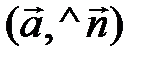 . (3.21)
. (3.21)
Объединяя результаты (3.20) и (3.21), получаем формулу
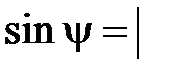 сos
сos 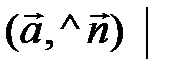 ,
,
которую мы будем применять при решении задач на нахождение угла между прямой и плоскостью векторно-координационным способом.
Координаты вектора 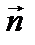 можно найти, не выходя за рамки школьной программы, например, следующим образом: если вектор
можно найти, не выходя за рамки школьной программы, например, следующим образом: если вектор 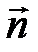
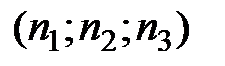 – нормальный вектор плоскости t, а векторы
– нормальный вектор плоскости t, а векторы 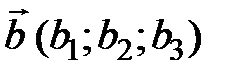 и
и 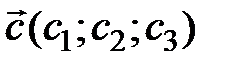 – векторы, параллельные плоскости t, то
– векторы, параллельные плоскости t, то 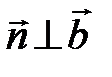 и
и 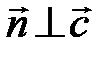 , т. е.
, т. е. 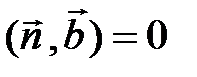 и
и 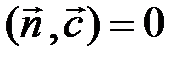 или
или
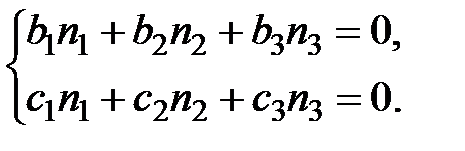
Из этой системы уравнений координаты 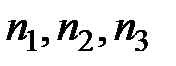 находятся с точностью до пропорциональности. Их можно принять за координаты нормального вектора плоскости t.
находятся с точностью до пропорциональности. Их можно принять за координаты нормального вектора плоскости t.
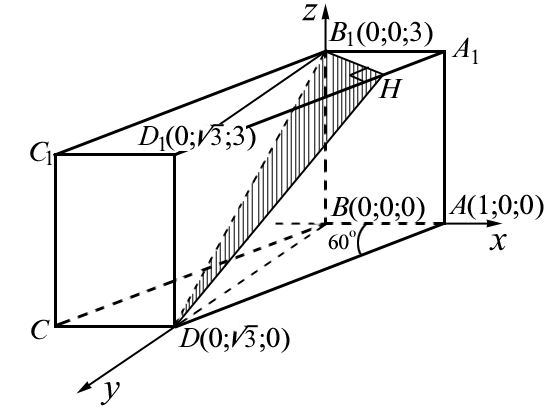
| Рис. 3.8 |
Решение. Зададим в пространстве прямоугольную систему координат Bxyz (рис. 3.8).
Воспользуемся для этого тем, что заданный параллелепипед прямой, т. е. BB 1 ^ BA и BB 1 ^ BD. Прямые BA и BB 1, таким образом, можно принять соответственно за оси Bx и Bz. Для задания оси By отметим, что в треугольнике ABD BD 2 = AB 2 + AD 2 – 2 AB × AD ×cos 60 °.
Положив AB = a, получаем, что тогда
AD = 2 a и BD 2 = a 2 + 4 a 2 – 2 a ×2 a ×cos 60 ° = 3 a 2.
Тогда в треугольнике ABD: AD 2 = AB 2 + BD 2, т. е. Ð ABD = 90 °.
Итак, прямую BD можно принять за ось By. Так как в заданном параллелепипеде AB: AA 1 = 1:3, и, как подсчитано выше, BD 2 = 3 a 2, т. е. BD = 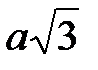 , то, принимая отрезок BA за единичный отрезок, координаты точек A, D и B 1 получим следующими: A (1; 0; 0),
, то, принимая отрезок BA за единичный отрезок, координаты точек A, D и B 1 получим следующими: A (1; 0; 0), 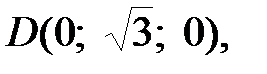 и B 1(0; 0; 3).
и B 1(0; 0; 3).
Определим в выбранной системе координат координаты точки D 1 и вектора 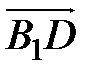 . Получим
. Получим 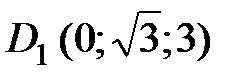 ,
, 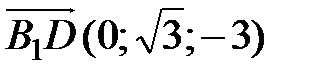 . Найдем далее координаты
. Найдем далее координаты 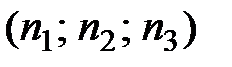 какого-нибудь вектора
какого-нибудь вектора 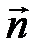 – нормального вектора плоскости
– нормального вектора плоскости 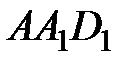 . Сделаем это исходя из следующих соображений: так как вектор
. Сделаем это исходя из следующих соображений: так как вектор 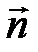 перпендикулярен плоскости AA 1 D 1, то
перпендикулярен плоскости AA 1 D 1, то 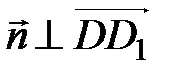 и
и 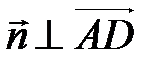 . Но
. Но 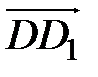 (0; 0; 3) и
(0; 0; 3) и 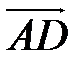
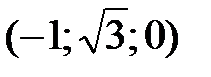 . Таким образом,
. Таким образом, 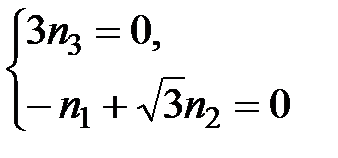 , откуда n 3 = 0 и, полагая, например,
, откуда n 3 = 0 и, полагая, например, 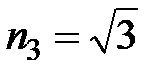 , находим n 1 = 3. Итак, в качестве нормального вектора плоскости AA 1 D 1 можно взять вектор
, находим n 1 = 3. Итак, в качестве нормального вектора плоскости AA 1 D 1 можно взять вектор 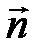
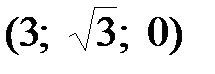 , тогда, обозначив искомый угол через y, получаем
, тогда, обозначив искомый угол через y, получаем
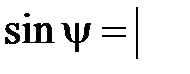
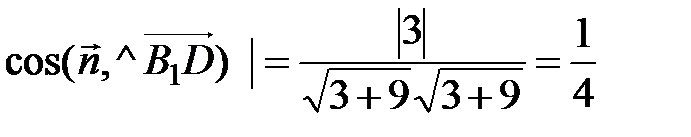 .
.
Это значит, что угол между прямой B 1 D и плоскостью грани AA 1 D 1 D равен 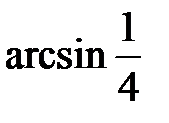 .
.
Ответ: угол между прямой B 1 D и плоскостью грани AA 1 D 1 D равен 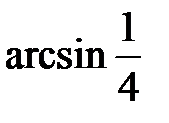 .
.
Векторно-координационный способ нахождения двугранного угла между плоскостями сводится к нахождению угла между их нормальными векторами.
Пример 15. На ребрах AC и SA правильного тетраэдра SABC взяты соответственно точки K и L – средины этих ребер. Через точки B, K и L проведена секущая плоскость. Найдем угол между плоскостями BKL и SAC.
Решение. Ведем систему координат Dxyz, как показано на рис. 3.9 (точка D – средина ребра AB).
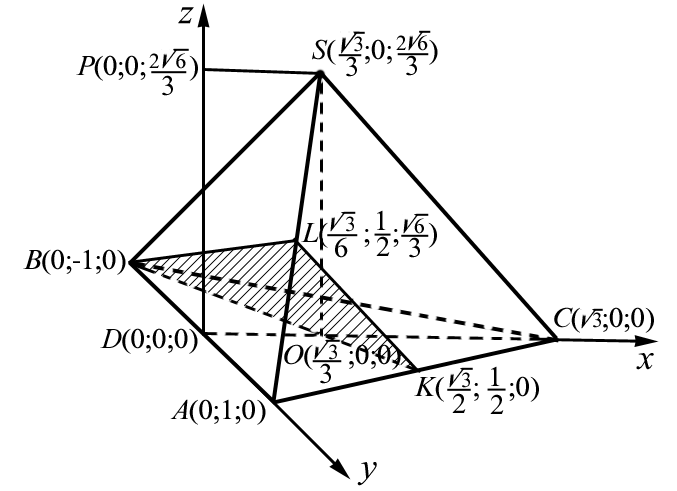
| Рис. 3.9 |
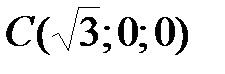 и
и 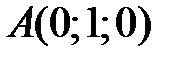 , затем точки
, затем точки 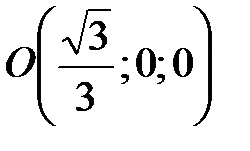 ,
, 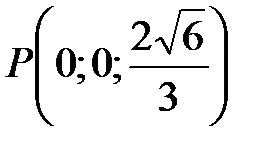 ,
, 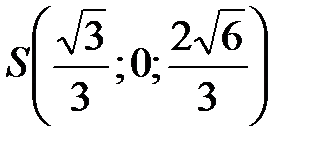 , далее
, далее 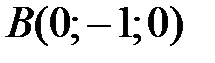 ,
, 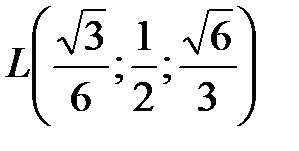 и
и 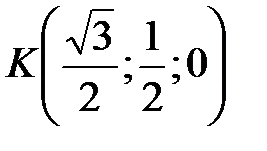 . Теперь найдем координаты векторов
. Теперь найдем координаты векторов 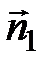 и
и 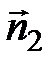 – нормальных векторов соответственно плоскостей BKL и SAC. Находим координаты
– нормальных векторов соответственно плоскостей BKL и SAC. Находим координаты 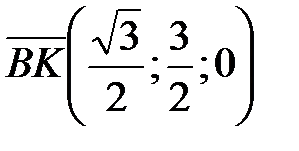 ,
, 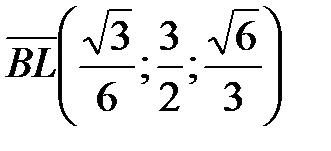 . Так как
. Так как 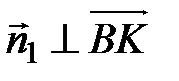 и
и 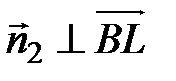 , то полагая
, то полагая 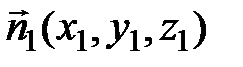 , получаем систему
, получаем систему 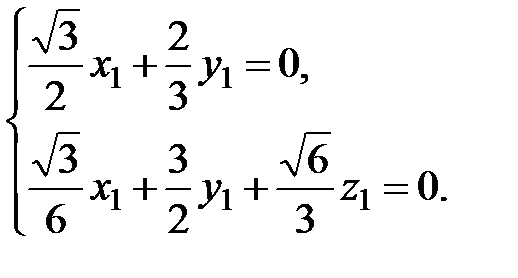
Из системы выражаем наши неизвестные координаты, например, через y 1, имеем 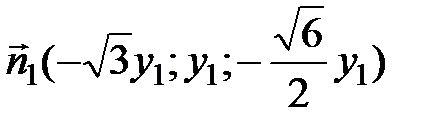 . Тогда с точностью до пропорциональности находим
. Тогда с точностью до пропорциональности находим 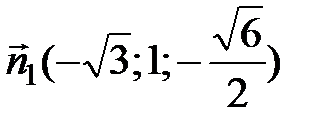 .
.
Аналогично находим и вектор 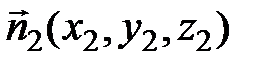 . Так как
. Так как 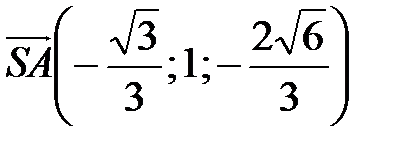 ,
, 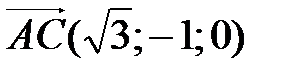 и
и 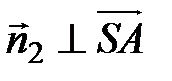 ,
, 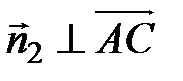 , то
, то
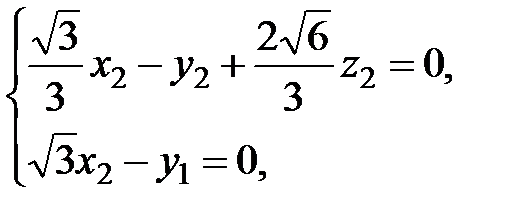
откуда 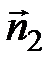
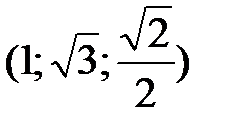 .
.
Обозначим для краткости угол между плоскостями BKL и SAC через j, находим
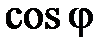 =
= 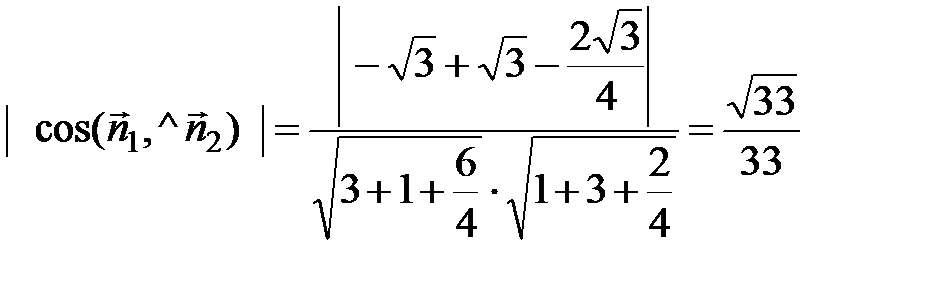 .
.
Таким образом, искомый угол равен 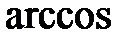
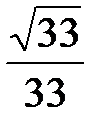 .
.
Ответ: 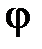 =
= 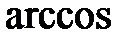
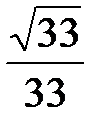 .
.
Вопросы и задания для самоподготовки
1. Какие векторы называются равными?
2. Сформулировать правило сложения любого числа векторов.
3. Какие векторы называются противоположными?
4. Какие векторы называются коллинеарными?
5. Назвать необходимое и достаточное условие коллинеарности векторов.
6. Назвать понятие прямоугольного базиса. Разложение вектора по базису 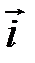 ,
, 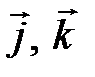 .
.
7. Назвать понятие координат вектора.
8. Как найти координаты вектора, заданного координатами точек – начала и конца этого вектора?
9. Чему равна длина (модуль) вектора, заданного своими координатами?
10. К чему сводятся линейные операции над векторами, заданными своими координатами?
11. Сформулировать условие коллинеарности двух векторов, заданными своими координатами.
12. Дать определение скалярного произведения двух векторов. Его свойства.
13. Когда скалярное произведение двух векторов больше нуля, меньше нуля?
14. Сформулировать условие перпендикулярности двух векторов.
15. Назвать выражение скалярного произведения через координаты векторов?
16. Назвать нахождение угла между двумя векторами.
3.4. Тесты по теме «Элементы векторной алгебры»
Дата публикования: 2015-09-17; Прочитано: 1230 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
