Коды Хэмминга

Коды Хэмминга позволяют исправлять одиночную ошибку в блоке. Для каждого числа проверочных символов 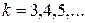существует классический код Хэмминга с маркировкой

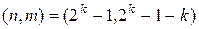, (8.57)

т.е. — (7,4), (15, 11), (31, 26)...

При других значениях числа информационных символов т получаются так называемые усеченные (или укороченные ) коды Хэмминга. Так, для международ­ного телеграфного кода МТК-2, имеющего 5 информационных символов, по­требуется использование корректирующего кода (9,5), являющегося усеченным от классического кода Хэмминга (15,11), так как число символов в этом коде уменьшается (укорачивается) на 6. Для примера рассмотрим код Хэмминга (7,4).

В простейшем варианте при заданных четырех (т= 4) информационных символах 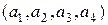будем полагать, что они сгруппированы в начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы тремя проверочными символами (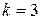), задавая их следующими равенствами проверки на четность, которые определяются соответствующими алгоритмами. Известно, что кодовое расстояние равно минимальному числу проверок, в которые входит информационный символ, плюс 1. В рассматриваемом коде . Следовательно, каждый информационный символ должен входить минимум в две проверки. Определим правило формирования проверочных символов следующим образом:

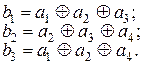(8.58)

В соответствии с этим алгоритмом определения значений проверочных символов 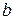в табл. 8.13 приведены все возможные 16 кодовых слов кода Хэмминга (7,4).

Таблица 8.13. Кодовые комбинации кода Хэмминга (7,4)

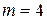
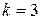
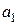
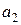
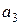
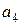
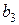
Составим производящую матрицу 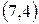в канонической форме

или 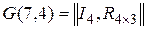(табл.8.14).

Таблица 8.14. Производящая матрица 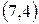в канонической форме

,

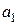
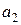
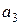
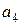
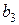
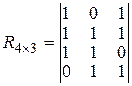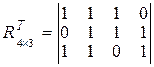
Составим проверочную матрицу

.

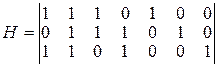Транспонированная проверочная матрица будет иметь вид

.

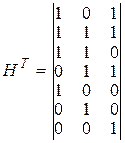Предположим, что на вход декодера для (7,4)-кода Хэмминга поступает кодовое слово

.

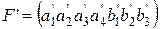Апостроф означает, что любой символ слова может быть искажен помехой в канале связи и возникает ошибка .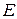

В декодере в режиме исправления ошибок строится последовательность:

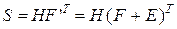(8.59)

где 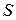– результат декодирования (синдром), который в данном случае является трехсимвольным.

Символы синдрома можно так же получить с использованием следующей процедуры

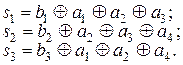(8.60)

В данном случае синдром 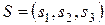представляет собой сочетание результатов проверки на четность соответствующих символов кодовой группы и характеризует определенную конфигурацию ошибок (вектор ошибок).

Число возможных синдромов определяется выражением

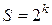. (8.61)

При числе проверочных символов 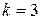имеется восемь возможных синдромов (2³ = 8). Нулевой синдром (000) указывает на то, что ошибки при приеме от­сутствуют или не обнаружены. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется. Классические коды Хэмминга имеют число синдромов, точно равное их необходимому числу, позволяют исправить все однократные ошибки в любом информативном и проверочном символах и включают один нулевой синдром. Такие коды называются плотноупакованными.

Для рассматриваемого кода (7,4) в табл. 8.15 представлены ненулевые синд­ромы и соответствующие конфигурации ошибок.

Таблица 8.15. Ненулевые синд­ромы и соответствующие конфигурации ошибок для кода (7,4)

Синдром
Конфи-гурация ошибок
Ошиб- ка в символе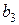

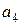
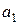
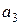
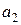
Для определения и исправления искаженного разряда можно использовать матрицу одиночных ошибок, состоящую из единичной матрицы размерности 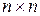, к которой приписывается транспонированная проверочная матрица.

.

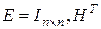При определении синдрома в проверочной матрице находится комбинация синдрома. Искаженный разряд – это разряд в данной строке, в которой стоит «1». Искаженный разряд исправляем посредством сложения строки в матрице ошибок полученной комбинации.

Пример. Для кода (7,4) задана комбинация .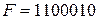

Составляется матрица одиночных ошибок

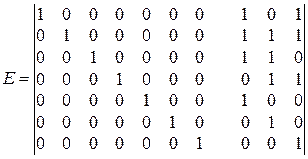
Под воздействием помех принята комбинация 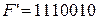- искажен третий разряд.

Определяем синдром

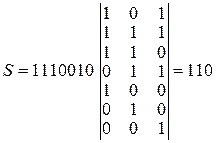
В проверочной матрице находим комбинацию 110.

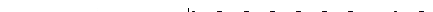
Прибавляем третью строку единичной матрицы к полученной комбинации .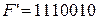

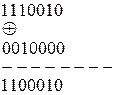
Сообщение исправлено.

Таким образом, код (7,4) позволяет исправить все одиночные ошибки. Прос­тая проверка показывает, что каждая из ошибок имеет свой единственный син­дром. При этом возможно создание такого цифрового корректора ошибок (де­шифратора синдрома), который по соответствующему синдрому исправляет соот­ветствующий символ в принятой кодовой группе. После внесения исправления проверочные символы 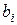на выход декодера не выводятся. Две или более ошибок превышают возможности корректирующего кода Хэмминга, и декодер будет ошибаться. Это означает, что он будет вносить неправильные ис­правления и выдавать искаженные информационные символы.

Идея построения подобного корректирующего кода, естественно, не меня­ется при перестановке позиций символов в кодовых словах. Все такие варианты также называются кодами Хэмминга (7,4). Часто проверочные разряды располагают не в начале или конце информационных разрядов, а в определенных местах. Рассмотрим методику построения такого кода на примере кода (7,4). Переведем номера разрядов в двоичную систему счисления и поставим им в соответствие проверочные и информационные разряды (табл.8.16).

Таблица 8.16. Места расположения информационных и проверочных разрядов и формирование проверочных разрядов для кода Хэмминга (7,4)

№ разряда	№ разряда в двоичной системе	Места расположения информационных и проверочных разрядов и формирование проверочных разрядов
		= + +
		= + +
		= + +

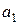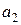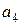
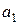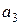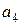
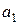
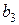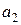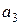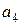
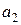
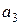
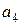
Т.е. 1-й проверочный разряд расположен там, где номер разряда имеет только одну 1 и к тому же на 1-м месте. Ему соответствует разряд под номером 1. Второй проверочный разряд расположен там, где номер разряда имеет так же только одну 1 и к тому же на 2-м месте. Ему соответствует разряд под номером 2. Третий проверочный разряд 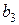расположен там, где номер разряда имеет так же только одну 1 и к тому же на 3-м месте. Ему соответствует разряд под номером 4. Оставшиеся разряды 3-й, 5-й, 6-й и 7-й заполняем информациоными разрядами.

Выпишем разряды, у которых первый разряд равен 1:

= 1, 3, 5, 7.

Выпишем разряды, у которых второй разряд равен 1:

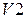= 2, 3, 6, 7.

Выпишем разряды, у которых третий разряд равен 1:

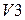= 4, 5, 6, 7.

Для получения первого проверочного разряда суммируем все разряды первой строки , кроме первого, т.е. 3, 5 и 7.

.

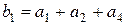Для получения второго проверочного разряда суммируем все разряды второй строки 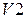, кроме первого, т.е. 3, 6, 7:

.

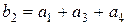Для получения третьего проверочного разряда суммируем все разряды третьей строки 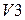, кроме первого, т.е. 5, 6, 7:

.

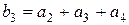При этом синдром укажет номер искаженного разряда. Так, если синдром равен 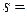0 1 1, то искажен третий разряд. Ему соответствует 1-й информационный символ.

Усеченные коды являются неплотно упакованными, так как число синдромов у них превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов будет равно 2⁴ =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5).

Рассмотрим методику формирования проверочных разрядов на примере усеченного кода (9,5). В коде (9,5) имеется 9 разрядов, 5 из которых являются информационными. Пронумеруем разряды в десятичной и двоичной системе счисления (табл.8.17). Номерам разрядов в двоичной системе будут соответствовать синдромы.

Таблица 8.17. Места расположения информационных и проверочных разрядов и формирование проверочных разрядов для кода Хэмминга (9,5)

Расположим проверочные разряды на тех позициях, которым соответствуют номера разрядов в двоичной системе с одной единицей, а именно расположим на 1-м месте (№ разряда в двоичной системе – 0001), на 2-м (0010), 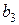на 4-м (0100) и 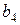на 8-м (1000). Информационные разряды расположим на оставшихся местах. Проверочный разряд получим суммированием информационных разрядов, которым соответствует номер с единицей в 1- разряде двоичной системы счисления 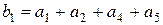. Проверочный разряд получим суммированием информационных разрядов, которым соответствует номер с единицей во 2- разряде двоичной системы 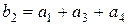. Аналогично 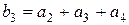и 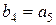. Для формирования разряда 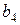остался один информационный разряд 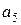, что характерно для усеченных кодов. Чтобы не было простого дублирования информационного разряда для формирования 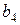возьмем еще какой-нибудь разряд, например, 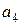, который также можно исключить из формирования . 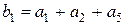Тогда , а 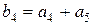. Если же мы исключили 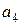из и ввели в 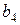, то его номер также должен быть изменен. Поэтому теперь 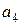соответствует номер 1110. Рассмотрим пример. Необходимо закодировать сообщение 1 1 0 1 0.

Имеется 5 информационных разрядов :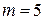

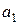
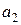
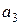
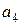
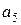
Рассчитаем количество проверочных разрядов

Маркировка кода Хэмминга .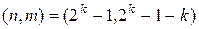

Необходимо, чтобы выполнялось условие: 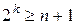, 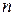– число полученных разрядов.

Если принять ,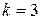

2³ =8;

тогда 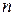=8-1=7; 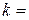7-5=2. 2² < 7+1 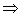неравенство не выполняется.

Примем ,

2⁴ =16;

тогда 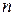=16-1=15; 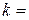15-5=10. 2¹⁰ ≥ 15+1 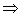неравенство выполняется.

2⁴ ≥ 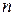+1, 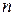=4+5=9.

Получен код (9,5).

Получим проверочные разряды

1 1 0 1 0

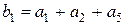=1+1+0=0;

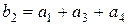=1+0+1=0;

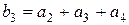=1+0+1=0;

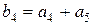=1+0=1.

Закодированное сообщение будет иметь вид:

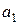
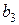
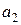
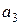
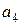
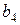
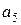
Проверочные разряды можно также получить при помощи суммирования номеров ненулевых информационных разрядов в двоичной системе. Для данного примера ненулевыми информационными разрядами являются 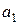, 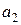и 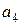. Им соответствуют номера разрядов 0 0 1 1, 0 1 0 1 и 1 1 1 0 соответственно. Просуммируем эти номера и получим проверочные разряды (табл. 8.18).

Таблица 8.18. Правило формирования проверочных разрядов

Разряд	№ разряда
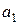
	0 0 1 1
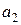
	0 1 0 1
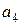
	1 1 1 0
Сумма	1 0 0 0
Проверочные разряды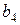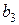

Пусть под воздействием помех в данной комбинации исказился 7=й разряд, т.е. 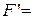0 0 1 0 1 0 0 1 0. Определяем синдром:

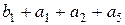=0+1+1+0=0;

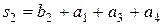=0+1+0+0=1;

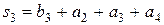=0+1+0+0=1;

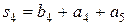=1+0+0=1.

Получен синдром 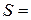1 1 1 0.

Смотрим в таблицу 8.17 и ищем синдром 1 1 1 0 и определяем, что ему соответствует 7-й разряд. Исправляем 7-й разряд 0 0 1 0 1 0 1 1 0. Сообщение исправлено. Исключаем проверочные символы: 1 1 0 1 0.

Расширенные коды Хэмминга получают в результате дополнения кодов с общей проверкой каждой из кодовых комбинаций на четность, т.е. еще одним проверочным символом. Это позволяет увеличить минимальное кодовое расстояние до .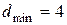

За показатель помехоустойчивости кода Хэмминга примем вероятность приёма кодовой комбинации с ошибками.

Расчёт вероятности ошибки произведём для семиэлементного кода, считая искажения символов в кодовых комбинациях равновероятными и независимыми.

Приём с ошибкой при применении кода Хемминга с исправлением одиночной ошибки будет в том случае, если искажено более одного символа. В соответствии с этим вероятность искажения кодовой комбинации равна

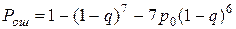, (8.62)

где 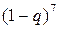- вероятность отсутствия искажений;

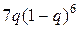- вероятность возникновения одной ошибки.