Вейвлеты

Представление случайных сигналов и изображений в виде ряда или преобразований Фурье малоэффективно. Это связано с тем, что базисная функция рядов Фурье - синусоида - определена в промежутке от 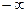до 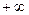и по своей природе является гладкой периодической функцией. Более эффективным решением является выбор принципиально нового базиса и класса функций-вейвлетов, используемых для декомпозиции и реконструкции функций и сигналов, в том числе нестационарных. Вейвлеты (wavelets) - это обобщенное название особых функций, которые имеют вид коротких волновых пакетов с нулевым интегральным значением и с той или иной, иногда очень сложной, формой. Такие функции локализованы на оси независимой переменной и способны к сдвигу по ней и масштабированию (растяжению / сжатию).

Вейвлеты создаются с помощью специальных базовых функций - прототипов, задающих их вид и свойства и отвечают ряду специфических условий. Набор вейвлетов, в их временном или в частотном представлении, может аппроксимировать сложный сигнал или изображение, причем идеально точно или с некоторой погрешностью.

Вейвлет-спектрограммы более информативные, чем Фурье-спектрограммы, и в отличие от последних, позволяют легко обнаружить сверхтонкие локальные особенности функций, сигналов и изображений.

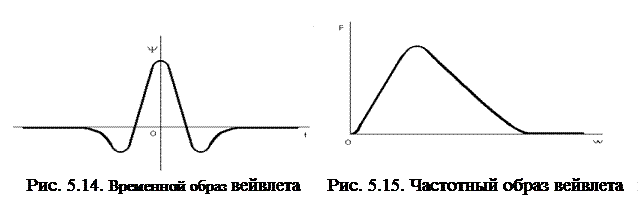
Сравнивая с тригонометрическими базисными функциями, которые более локализованы в частотной области, но совсем не локализованы во временной области, а также с некоторой импульсной базисной функцией (функцией Кронекера), которая четко локализована во временной области, но совсем не несет никакой информации о частоте сигнала, вейвлеты занимают промежуточное положение и характеризуются своим временным (рис. 5.14) и частотным образами (рис. 5.15). Временной образ определяется некоторой функцией времени 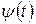(psi-функцией). Частотный образ определяется функцией-образом 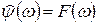(Фурье-образом), который задает огибающую спектра вейвлета. Фурье-образ определяется выражением:.

.

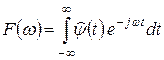Для демонстрации этих параметров удобно использовать вейвлет типа «мексиканский шляпа». Его временной образ, в отличие от большинства других вейвлетов, описывается аналитическим выражением

.

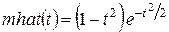Очевидно, что указанный вейвлет напоминает затухающее синусоидальное колебание с некоторой «средней частотой» и плоскостью (над осью времени и под ней) близкой к нулю. Точное нулевое значение плоскости (над осью времени и под ней) - одно из важнейших условий, которое позволяет отнести временную зависимость 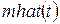к вейвлетам. Если вейвлет в пространстве сужается, его «средняя частота» увличивается, спектр вейвлета перемещается в зону более высоких частот и расширяется.

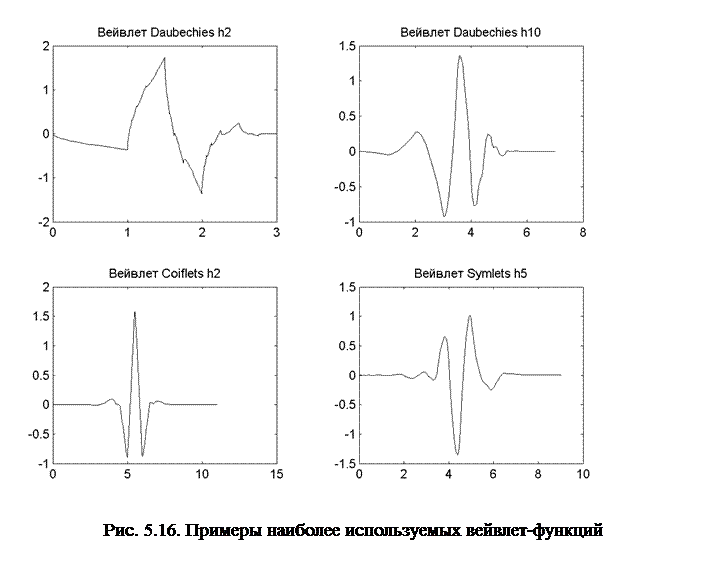
Существует большое количество разновидностей вейвлетов, которые отличаются как по форме так и по количеству базисных коэффициентов. Примеры наиболее используемых вейвлет-функций приведены на рис. 5.15.

С помощью вейвлетов сигнал представляется совокупностью волновых пакетов - вейвлетов, образованных на основе полной первоначальной (базовой) функции 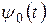. Эта совокупность, различная в разных частях временного промежутка определения сигнала и корректируемая множителями, иногда имеет вид сложных временных функций, и представляет сигнал с той или иной степенью детализации. Такой подход называется вейвлет-анализом сигналов.

Количество вейвлетов, которые используются в процессе разложения сигнала, задает уровень декомпозиции сигнала. За нулевой уровень декомпозиции чаще всего принимают сам сигнал, а последующие уровни декомпозиции образуют вейвлет-дерево того или иного вида. Точность представления сигнала при переходе на более низкой уровень декомпозиции снижается, однако появляется возможность вейвлет-фильтрации сигналов, изъятие шумов и эффективной компрессии сигналов. Иными словами становится возможной вейвлет-обработка сигналов.

Одна из фундаментальных идей вейвлет-представления сигналов заключается в разделении на две составляющие приближения к сигналу: грубую (аппроксимирующую) и уточняющую (детализирующую), с последующим их уточнением итерационным методом. Каждый шаг такого уточнения соответствует определенному уровню декомпозиции и реставрации сигнала. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами.

В основе непрерывного вейвлет-преобразования НВП (или CWT - Continue Wavelet Transform) лежит использование двух непрерывных и интегрированных по всей оси 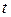функций:

- вейвлет-функции 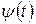с нулевым значением интеграла 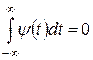, которая определяет составляющие сигнала и порождает детализирующие коэффициенты;

- масштабируемой или скрейлинг-функции 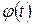с единичным значением интеграла 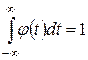, которая определяет грубое приближение (аппроксимацию) сигнала и которая порождает коэффициенты аппроксимации.

Phi-функции 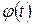присущи далеко не всем вейвлетам, а только тем, которые относятся к ортогональным.

Psi-функция 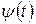формируется на основе той или иной базисной функции 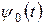, которая как и 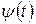, определяет тип вейвлета. Базисная функция должна соответствовать требованиям, определенным для psi-функции 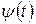и обеспечивать выполнение двух основных операций:

- сдвиг по оси времен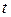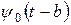и : при ;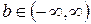

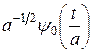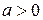- масштабирование при и .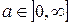

Параметр 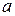задает ширину этого пакета, а 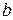- его положение. Нетрудно убедиться, что следующее выражение задает одновременно два этих свойства функции :

.

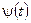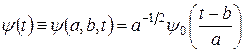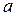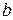Итак, для приведенных и функция 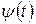и является вейвлетом. Вейвлеты с пометкой 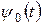, иногда называют «материнскими вейвлетами», поскольку они порождают целый ряд вейвлетов определенного вида. О вейвлетах, которые четко локализованы в пространстве (или во времени), говорят, что они имеют компактный носитель.

Прямое непрерывное вейвлет-преобразования (ПНВП) сигнала 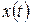задается, по формальной аналогии с преобразованием Фурье, путем вычисления вейвлет-коэффициентов по формуле:

,

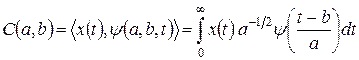где 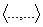- скалярное произвеление соответствующих множителей, а границы интегрирования учитывают ограничения .

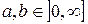Прямое вейвлет-преобразование можно рассматривать как разложение сигнала по всем возможным сдвигам и растяжение/ сжатие сигнала 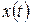или некоторой произвольной функции. При этом параметры 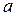и 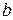могут принимать любые значения в пределах указанных выше областей их определения. Отметим, что прямое преобразование Фурье также можно рассматривать как разложение за сдвигами (подразумевается фазовый сдвиг гармоник, которые задают положение их графиков) и растяжения/сжатия (которые определяются значениями амплитуд гармоник), но применительно к одной функции (синусоиды), что не очень удобно для акцентирования локальных особенностей сигналов.

Обратное непрерывное вейвлет-преобразование (ОНВП) осуществляется по формуле реконструкции во временной области:

,

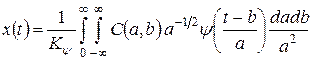где 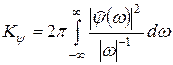- константа, которая определяется только функцией .

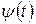Частотное (спектральное) представление вейвлетов имеет важное значение для определения фильтрующих свойств вейвлет-преобразований и алгоритма быстрого вейвлет-преобразования (БВП).

Согласно такому подходу частотная область вейвлетов может быть разделена на две составляющие - низкочастотную и высокочастотную. Их частота разделения равна половине частоты дискретизации сигнала. Для их разделения достаточно использовать два фильтра: низкочастотный 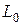и высокочастотный 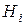, к входам которых подается сигнал. Фильтр 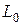дает частотный образ для аппроксимации (грубого приближения) сигнала, а фильтр 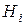- для его детализации.

Поскольку фильтры передают только половину всех частотных компонентов сигнала, то компоненты, которые не попали в полосу прозрачности можно изъять. Эта операция получила название «децимации».

Однако фильтр 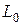можно, в свою очередь, разложить на два фильтра и вновь подвергнуть спектры этих новых фильтров операции децимации. Это означает изменения реконструкции. Таким образом, можно сформировать систему вейвлет-фильтров, которые реализуют операцию декомпозиции сигнала того или иного уровня.

Подобные операции в конце концов сокращают спектр соответствующих компонентов сигнала и представляют собой основу приблизиженного представления сигнала на разных уровнях его декомпозиции. Такое представление необходимымо, например, для реализации операции сжатия сигналов и их очистки от шума. Операция последовательного «расклеивания» фильтров и постепенного огрубения представления сигнала получила название алгоритма Малла (в честь французского ученого Mallat).