 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прямолінійні твірні поверхонь другого порядку
|
|
Введемо поняття прямолінійних твірних поверхонь другого порядку.
Означення 3. Пряму, кожна точка якої належить поверхні, називають прямолінійною твірною цієї поверхні.
Очевидно, що кожна твірна циліндричної та конічної поверхні є її прямолінійною твірною. Дослідимо питання існування прямолінійних твірних у випадку інших поверхонь. Не розглядаючи поверхні еліпсоїда, двопорожнинного гіперболоїда та еліптичного параболоїда, для яких, очевидно, прямолінійних твірних не існує, зупинимось на випадку однопорожнинного гіперболоїда. Розглянемо його канонічне рівняння 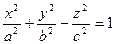 , яке запишемо у виді
, яке запишемо у виді
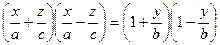 . (6)
. (6)
Крім цього розглянемо системи рівнянь
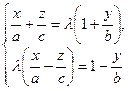 (7)
(7)
та
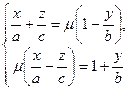 , (8)
, (8)
де 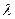 та
та 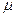 – довільні числові параметри. Кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Оскільки дві довільні площини з кожної системи перетинаються, то обидві системи задають
– довільні числові параметри. Кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Оскільки дві довільні площини з кожної системи перетинаються, то обидві системи задають 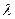 – та
– та 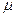 – параметричні множини прямих. Очевидно, що кожний розв’язок систем (7) та (8) задовольняє рівняння (6), тому ці системи задають
– параметричні множини прямих. Очевидно, що кожний розв’язок систем (7) та (8) задовольняє рівняння (6), тому ці системи задають 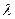 – та
– та 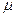 – параметричні сім’ї прямолінійних твірних однопорожнинного гіперболоїда.
– параметричні сім’ї прямолінійних твірних однопорожнинного гіперболоїда.
Будемо вважати, що системи (7) та (8) містять, як частинні випадки, рівняння прямих
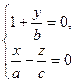 та
та 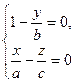 .
.
Їх не можна отримати із даних систем при будь-яких скінчених значеннях параметрів 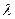 та
та 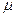 , але можна розглядати, як результат граничного переходу в системах
, але можна розглядати, як результат граничного переходу в системах
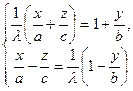 та
та 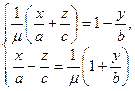
при 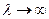 та
та 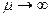 .
.
Доведемо наступне твердження.
Теорема. Через кожну точку однопорожнинного гіперболоїда проходить рівно по одній прямій з кожної 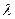 – та
– та 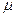 – параметричних сімей прямих (7) та (8). Дві довільні прямолінійні твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, при умові
– параметричних сімей прямих (7) та (8). Дві довільні прямолінійні твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, при умові 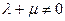 перетинаються.
перетинаються.
Доведення. Нехай точка 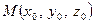 належить поверхні. Тоді її координати задовольнятимуть як рівняння (6), так і системи (7) та (8), в яких значення параметрів
належить поверхні. Тоді її координати задовольнятимуть як рівняння (6), так і системи (7) та (8), в яких значення параметрів 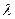 та
та 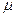 потрібно вибрати, як розв’язки рівнянь, одержаних із систем після підставляння координат точки
потрібно вибрати, як розв’язки рівнянь, одержаних із систем після підставляння координат точки 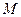 . Таким чином, через кожну точку поверхні проходить хоча б по одній прямій з кожної
. Таким чином, через кожну точку поверхні проходить хоча б по одній прямій з кожної 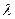 та
та 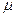 – параметричних сімей прямолінійних твірних.
– параметричних сімей прямолінійних твірних.
Тепер припустимо, що через точку 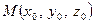 проходить дві різні прямі
проходить дві різні прямі
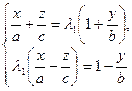 та
та 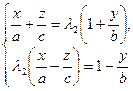 ,
,
визначені системою (7) при різних значеннях параметрів 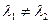 . Тоді з рівностей
. Тоді з рівностей
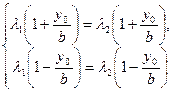
випливає, що 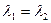 , що суперечить припущенню. Цим самим показано, що дві різні прямі, визначені системою (7) (аналогічно системою (8)), не можуть мати спільних точок.
, що суперечить припущенню. Цим самим показано, що дві різні прямі, визначені системою (7) (аналогічно системою (8)), не можуть мати спільних точок.
Для того, щоб встановити, як розташовані дві прямолінійні твірні, визначені різними системами, дослідимо на сумісність систему, утворену із рівнянь систем (7) та (8). Використовуючи відомі методи лінійної алгебри, знайдемо ранги основної та розширеної матриць, складених із коефіцієнтів біля змінних та вільних членів.
Отримуємо
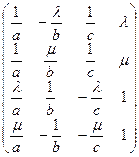
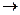
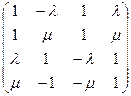
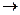
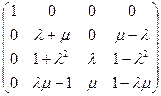 .
.
Якщо 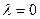 або
або 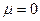 , але
, але 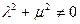 , то легко бачити, що ранги матриць рівні, тобто система рівнянь сумісна. Якщо ж
, то легко бачити, що ранги матриць рівні, тобто система рівнянь сумісна. Якщо ж 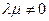 , то одержану матрицю можна звести до виду
, то одержану матрицю можна звести до виду
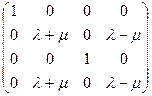 ,
,
звідки видно, що якщо 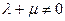 , то ранги матриць рівні, тобто система рівнянь сумісна, а прямолінійні твірні перетинаються. При
, то ранги матриць рівні, тобто система рівнянь сумісна, а прямолінійні твірні перетинаються. При 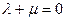 ранги матриць різні, тому система несумісна. Теорема доведена.
ранги матриць різні, тому система несумісна. Теорема доведена.
Встановимо, як розташовані прямі у випадку 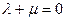 . Для цього ще раз розглянемо системи (7) та (8), поклавши у системі (8)
. Для цього ще раз розглянемо системи (7) та (8), поклавши у системі (8) 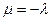 . Знайдемо напрямні вектори
. Знайдемо напрямні вектори 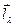 та
та 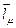 прямих (7) та (8), як векторні добутки векторів, перпендикулярних до площин, при перетині яких утворюються прямі. Маємо
прямих (7) та (8), як векторні добутки векторів, перпендикулярних до площин, при перетині яких утворюються прямі. Маємо
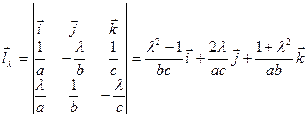 ,
,
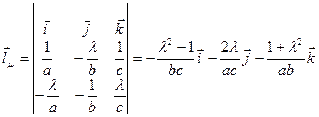 .
.
Як бачимо, вектори 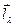 та
та 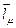 колінеарні, тому прямі (7) та (8) паралельні. Зауважимо, що на даний факт не звернули увагу автори [1], що привело до невірного формулювання теореми 2 у §169.
колінеарні, тому прямі (7) та (8) паралельні. Зауважимо, що на даний факт не звернули увагу автори [1], що привело до невірного формулювання теореми 2 у §169.
Нехай гіперболічний параболоїд заданий рівнянням 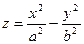 . Запишемо це рівняння у виді
. Запишемо це рівняння у виді
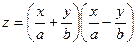 . (9)
. (9)
Розглянемо системи рівнянь
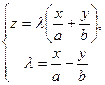 (10)
(10)
та
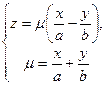 , (11)
, (11)
де 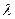 та
та 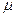 – довільні параметри. Як і в попередньому випадку, кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Дві довільні площини, які задаються рівняннями кожної системи, перетинаються, тому ці системи задають
– довільні параметри. Як і в попередньому випадку, кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Дві довільні площини, які задаються рівняннями кожної системи, перетинаються, тому ці системи задають 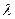 та
та 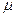 – параметричні множини прямих. Очевидно, що кожний розв’язок систем (10) та (11) задовольняє рівняння (9), тому вони задають
– параметричні множини прямих. Очевидно, що кожний розв’язок систем (10) та (11) задовольняє рівняння (9), тому вони задають 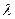 та
та 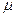 – параметричні сім’ї прямолінійних твірних гіперболічного параболоїда.
– параметричні сім’ї прямолінійних твірних гіперболічного параболоїда.
Через кожну точку гіперболічного параболоїда проходить рівно по одній прямій з кожної 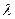 та
та 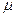 – параметричних сімей прямих (10) та (11). Дві довільні прямолінійні твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, перетинаються. Справді, припустимо, що через точку
– параметричних сімей прямих (10) та (11). Дві довільні прямолінійні твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, перетинаються. Справді, припустимо, що через точку 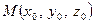 проходить дві різні прямі
проходить дві різні прямі
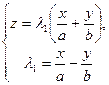 та
та 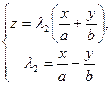 ,
,
одержані із системи (10) при 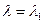 та
та 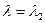 . Тоді з других рівнянь систем випливає, що
. Тоді з других рівнянь систем випливає, що 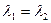 , що вказує на помилковість припущення. Оскільки дві різні прямі, визначені системою (10), не можуть мати спільних точок і не паралельні, то вони мимобіжні. Аналогічні міркування здійснюються у випадку системи (11).
, що вказує на помилковість припущення. Оскільки дві різні прямі, визначені системою (10), не можуть мати спільних точок і не паралельні, то вони мимобіжні. Аналогічні міркування здійснюються у випадку системи (11).
У випадку двох прямолінійних твірних, визначених різними системами, висновок про їхній перетин випливає із сумісності системи
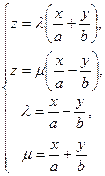 ,
,
розв’язком якої є 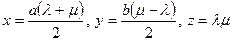 .
.
Зауважимо, що прямолінійні твірні розглянутих вище поверхонь мають технічні застосування. Зокрема, несучі конструкції даху олімпійського зимового палацу в японському місті Саппоро, який має форму гіперболічного параболоїда, зроблені у вигляді металевих балок, які є прямолінійними твірними поверхні. Конструкції з металевих балок, які зафіксовані так, як проходять прямолінійні твірні однопорожнинного гіперболоїда обертання, використовуються при будівництві водонапірних башт, телевізійних вишок.
Дата публикования: 2015-09-17; Прочитано: 3254 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
