 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ортонормовані базиси. Довжина вектора
|
|
Розглядаючи базис 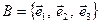 простору
простору 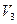 , ми накладали на базисні вектори тільки умови упорядкованості та лінійної незалежності. У деяких прикладних задачах обчислення суттєво спрощуються, якщо базисні вектори одиничні та взаємно перпендикулярні.
, ми накладали на базисні вектори тільки умови упорядкованості та лінійної незалежності. У деяких прикладних задачах обчислення суттєво спрощуються, якщо базисні вектори одиничні та взаємно перпендикулярні.
Означення 5. Базис 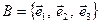 називають прямокутним декартовим або ортонормованим, якщо вектори базису одиничні та взаємно перпендикулярні.
називають прямокутним декартовим або ортонормованим, якщо вектори базису одиничні та взаємно перпендикулярні.
Щоб відрізняти ортонормовані базиси від інших використовують спеціальні позначення базисних векторів: 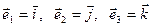 . Отже, згідно з означенням, базис
. Отже, згідно з означенням, базис 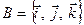 є прямокутним декартовим, якщо
є прямокутним декартовим, якщо 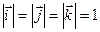 та
та 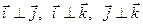 .
.
У просторі 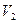 ортонормованим буде базис
ортонормованим буде базис 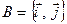 .
.
 Нехай в ортонормованому базисі
Нехай в ортонормованому базисі 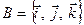 задано вектор
задано вектор 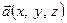 та нехай
та нехай 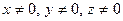 . Відкладемо від деякої точки
. Відкладемо від деякої точки 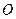 вектори
вектори 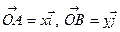 ,
, 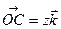 ,
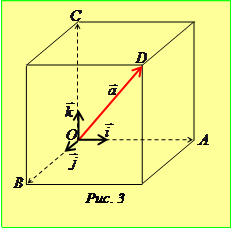
, 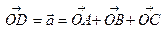 (рис. 3). Очевидно, що вектор
(рис. 3). Очевидно, що вектор 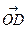 співпадає з діагоналлю прямокутного паралелепіпеда, побудованого на векторах
співпадає з діагоналлю прямокутного паралелепіпеда, побудованого на векторах 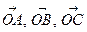 , як на сторонах. Оскільки довжини сторін паралелепіпеда дорівнюють
, як на сторонах. Оскільки довжини сторін паралелепіпеда дорівнюють
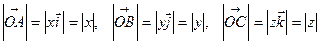 ,
,
то за відомою властивістю діагоналі прямокутного паралелепіпеда дістаємо 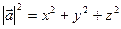 , звідки
, звідки
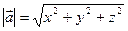 . (3)
. (3)
Одержана формула дозволяє обчислювати довжину вектора, знаючи його координати. Відмітимо, що коли одна або дві координати вектора 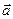 рівні нулю, то при обчисленні його довжини замість довжини діагоналі прямокутного паралелепіпеда доводиться шукати довжину діагоналі прямокутника або довжину вектора, який колінеарний до одного із базисних векторів. В обох випадках дістаємо співвідношення, які є частинним випадком формули (3).
рівні нулю, то при обчисленні його довжини замість довжини діагоналі прямокутного паралелепіпеда доводиться шукати довжину діагоналі прямокутника або довжину вектора, який колінеарний до одного із базисних векторів. В обох випадках дістаємо співвідношення, які є частинним випадком формули (3).
У просторі 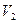 з вибраним у ньому ортонормованим базисом
з вибраним у ньому ортонормованим базисом 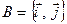 довжину вектора
довжину вектора 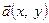 обчислюють за формулою
обчислюють за формулою 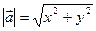 .
.
Дата публикования: 2015-09-17; Прочитано: 937 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
