 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Координати вектора. Дії над векторами у координатній формі
|
|
Розглянемо простір векторів 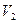 та деякий його базис
та деякий його базис  . Довільний вектор
. Довільний вектор 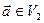 можна розкласти за цим базисом, тобто представити у вигляді
можна розкласти за цим базисом, тобто представити у вигляді
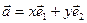 . (2)
. (2)
Насамперед зауважимо, що таке представлення єдине. Справді, припустимо, що розклад вектора 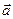 можливий із іншими коефіцієнтами, тобто нехай
можливий із іншими коефіцієнтами, тобто нехай 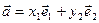 . Віднімаючи від даної рівності рівність (2), дістаємо
. Віднімаючи від даної рівності рівність (2), дістаємо 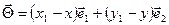 . Оскільки вектори
. Оскільки вектори 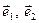 лінійно незалежні, то одержана рівність можлива тільки при нульових коефіцієнтах. Тому
лінійно незалежні, то одержана рівність можлива тільки при нульових коефіцієнтах. Тому 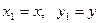 .
.
Означення 4. Коефіцієнти 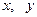 біля базисних векторів у рівності (1) називають координатами вектора
біля базисних векторів у рівності (1) називають координатами вектора 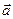 відносно базису
відносно базису  .
.
Координати вектора записують у вигляді 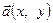 або
або 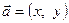 .
.
У випадку векторного простору 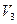 та деякого його базису
та деякого його базису 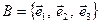 для довільного вектора
для довільного вектора 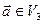 його координати визначаються, як коефіцієнти
його координати визначаються, як коефіцієнти  біля базисних векторів у рівності
біля базисних векторів у рівності 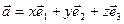 . Зауважимо, що таке представлення теж єдине. Записують
. Зауважимо, що таке представлення теж єдине. Записують  або
або 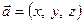 .
.
Два вектори, задані своїми координатами, рівні тоді і тільки тоді, коли їхні відповідні координати рівні.
Справді, у випадку векторного простору 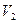 , з рівностей
, з рівностей 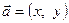
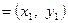 або
або 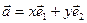
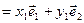 , випливає
, випливає 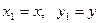 , оскільки вектори
, оскільки вектори 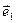 та
та  лінійно незалежні.
лінійно незалежні.
Аналогічні міркування реалізуються у випадку простору 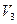 .
.
Розглянемо, як виконувати лінійні операції над векторами, що задані своїми координатами. Нехай задані два вектори  та
та 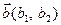 . Тоді
. Тоді
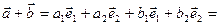
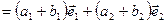 ,
,
тобто
 .
.
Аналогічно доводяться рівності
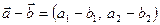
та
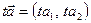 ,
,
де 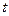 – довільний числовий множник.
– довільний числовий множник.
Так само, як і в просторі 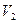 , у просторі
, у просторі 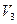 додавання та віднімання векторів, а також множення векторів на числа здійснюється виконанням відповідних операцій над координатами векторів.
додавання та віднімання векторів, а також множення векторів на числа здійснюється виконанням відповідних операцій над координатами векторів.
Теорема 7. Два вектори, задані своїми координатами, колінеарні тоді і тільки тоді, коли їхні координати пропорційні.
Доведення. Нехай задані два колінеарні вектори 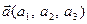 та
та 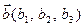 . Тоді вони лінійно залежні та існує число
. Тоді вони лінійно залежні та існує число 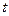 таке, що виконується рівність
таке, що виконується рівність 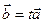 . Вона рівносильна координатним рівностям
. Вона рівносильна координатним рівностям 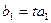 ,
, 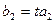 ,
, 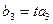 . Якщо
. Якщо 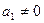 ,
, 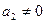 ,
, 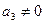 , то із попередніх рівностей випливає, що
, то із попередніх рівностей випливає, що  , тобто координати векторів пропорційні. Якщо деякі з координат одного із векторів рівні нулю, то відповідні координати у другого колінеарного до нього вектора теж дорівнюють нулю.
, тобто координати векторів пропорційні. Якщо деякі з координат одного із векторів рівні нулю, то відповідні координати у другого колінеарного до нього вектора теж дорівнюють нулю.
Навпаки, якщо виконуються рівності  , то, прирівнявши дані відношення до
, то, прирівнявши дані відношення до 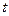 , дістаємо
, дістаємо 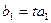 ,
, 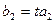 ,
, 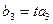 . Звідси випливає рівність
. Звідси випливає рівність 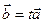 , яка означає колінеарність векторів
, яка означає колінеарність векторів 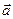 та
та 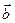 .
.
Дата публикования: 2015-09-17; Прочитано: 1216 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
