Многомерный анализ

Корреляционный анализ. Корреляционный анализ обеспечивает: а) измерение степени связи двух или более явлений; б) отбор факторов, оказывающих наиболее существенное влияние на результативный признак на основании измерения степени связности между явлениями; в) обнаружение ранее неизвестных причинных связей (кoрреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает численное значение этих связей и достоверность суждений об их наличии).

При проведении корреляционного анализа вся совокупность рассматривается как множество переменных (факторов), каждая из которых содержит n наблюдений; х_ik - наблюдение i переменной k; - значение k -ой переменной; i=1,...,n.. Основными средствами анализа являются: парные, частные коэффициенты корреляции, множественные коэффициенты корреляции.

Парные коэффициенты корреляции опосредованно учитывают влияние других факторов. Для исключения этого влияния определяют частные коэффициенты корреляции.

Парный коэффициент корреляции между k -м и L -м факторами вычисляется как

.

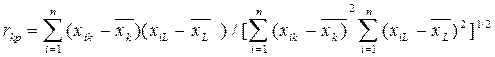Он служит показателем тесноты линейной статистической связи, но только в случае совместной нормальной распределенности случайных величин, выборками которых являются k -й и L -й факторы.

При этих же предпосылках для проверки гипотезы о равенстве нулю парного коэффициента корреляции используется t -статистика, распределенная по закону Стьюдента с п-2 степенями свободы. Сначала рассчитывается критическое значение t -статистики, а на его основе критическое значение коэффициента корреляции рассчитывается как

.

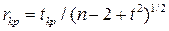Если расчетное значение больше критического, то гипотеза о равенстве нулю данного коэффициента корреляции отвергается на соответствующем вероятностном уровне. Аналогичные выводы имеют место при проверке значимости частных коэффициентов корреляции.

Частный коэффициент корреляции первого порядка между k -м и L -м факторами характеризует тесноту их линейной связи при фиксированном значении j -го фактора. Он определяется как

.

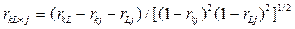Он распределен аналогично парному коэффициенту при тех же предпосылках, и для проверки его значимости используется t -статистика, но в которой число степеней свободы равно n-З. Частный коэффициент корреляции рассчитывается в общем виде и при условии, что все остальные переменные – фиксированные, следующим образом:

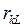(частн.) ,

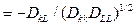где D_ij - определитель матрицы, образованной из мaтрицы парных коэффициентов корреляции вычеркиванием i -й строки и j –го столбца.

Для каждого частного коэффициента корреляции аналогично парному рассчитываются t -значение для проверки значимости коэффициента, а также доверительные интервалы. При этом дисперсия преобразованной величины равняется 1/(n-L-3), где L - число фиксированных переменных (в программе L=m-2).

Для определения тесноты связи между текущей k -й переменной и оставшимися (объясняющими) переменными используется выборочный множественный коэффициент корреляции:

,

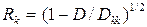где D – определитель матрицы парных коэффициентов корреляции.

Для проверки статистической значимости коэффициента множественной

корреляции используется величина

,

имеющая F - распределение с L и (n-L-2) степенями свободы соответственно.

Если рассчитанное F -значение больше значения F -распределения на соответствующем вероятностном уровне (0.9 и выше), то гипотеза о линейной связи между k -й переменной и остальными переменными не отвергается. В программе для каждого коэффициента множественной корреляции выводится F -значение и процентная точка F -распределения, которая ему соответствует.

Регрессионный анализ. При регрессионном анализе решаются следующиезадачи: а) установление форм зависимости (положительная, отрицательная, линейная, нелинейная); б) определение функции регрессии. Важно не только указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов - причин, если прочие (второстепенные, побочные) факторы не изменялись (находились на одном и том же среднем уровне), и если были бы исключены случайные элементы; в) оценка неизвестных значений зависимой переменной.

Уравнение множественной линейной регрессии имеет вид:

.

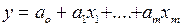В каждом виде регрессионного анализа необходимо выбрать зависимую переменную Y (для которой строится уравнение регрессии) и одну или несколько независимых переменных х_j (i=1,2,... m). Это уравнение позволяет установить статистическую взаимосвязь изучаемых показателей и, в случае ее устойчивости, давать аналитические и прогнозные оценки.

На базовом периоде времени строится уравнение зависимой переменной. Далее производится расчет прогнозных значений зависимой переменной по рассчитанному уравнению регрессии. При этом для всех регрессоров заранее должны быть получены их прогнозные оценки и дописаны в конец исходных данных. Для зависимой переменной в исходных данных на глубину периода прогнозирования необходимо дописать нулевые значения.

Различают различные виды множественной регрессии – линейную, пошаговую, гребневую и др.

В линейном регрессионном анализе рассматривается зависимость случайной величины Y от ряда исходных факторов (регрессоров) Х₁,Х₂,,...,Х_m, которая в силу влияния неучтенных факторов будет стохастической. В матричной записи она имеет вид:

,

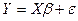где Y - вектор значений переменной, Х – матрица независимых переменных, β - подлежащий определению вектор параметров; ε- вектор случайных отклонений.

В регрессионном анализе действуют следующие предположения:

M[e_i × e_j] = 0, j ¹ 1, M[e_i × e_j] = s²_e, j = 1, …, m,

Матрица Х детерминирована и столбцы ее линейно независимы.

МНК-оценки находятся из условия минимума функционала:

(Y - Xb)^T (Y - Xb).

Оценки параметров имеют вид:

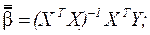
и являются несмещенными и эффективными.

Если - эмпирическая аппроксимирующая регрессия, то элементы вектора 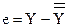- называются остатками. Анализ остатков позволяет судить о качестве построенного уравнения регрессии.

Пошаговая регрессия является одним из методов определения наилучшего подмножества регрессоров для объяснения Y. Реализуется пошаговая процедура с последовательным включением переменных в уравнение регрессии.

Пусть в уравнение регрессии включено L переменных, т.е. сделано L шагов алгоритма, и осуществляется L+1 шаг. Основной вопрос, который решается на каждой итерации - это вопрос о том, какую переменную включать в уравнение регрессии.

Для каждой переменной регрессии, за исключением тех переменных, которые уже включены в модель, рассчитывается величина C_j, равная относительному уменьшению суммы квадратов зависимой переменной. При включении переменной в уравнение регрессии она интерпретируется как доля оставшейся дисперсии независимой переменной, которую объясняет j -я переменная. Пусть k - номер переменной, имеющей максимальное значение j -го элемента. Тогда, если С_j < р, где р - определенная константа, то анализ переменных прекращается, и больше переменных не вводится в модель. В противном случае k- я переменная вводится в уравнение регрессии. Константа р является параметром метода и может быть изменена пользователем.

Гребневая регрессия основана на гребневых оценках, направленных на оценивание множественных линейных регрессий в условиях мультиколлинеарности, т.е. сильной корреляции независимых переменных.

Как известно, следствием мультиколлинеарности является обусловленность матрицы X’X и бесконечное возрастание по этой причине дисперсии оценок линейной регрессии.

Матрица X’X регуляризуется путем добавления малого положительного числа к диагональным элементам. В программе реализован алгоритм построения однопараметрической гребневой оценки вида

a(k) = (X’X + kD)X’Y, k³0,

где k – параметр регуляризации; D – матрица регуляризации, в качестве которой может быть выбрана единичная матрица или диагональная матрица, составленная из диагональных элементов X’X.

Для автоматического расчета параметра k выбрана формула

k = ms/a’a,

где а – вектор оценок регрессии по МНК, s - оценка остаточной дисперсии по МНК.

Парная регрессия устанавливает связь между откликом Y и функцией, зависящей от входной переменной X, т.е. регрессия имеет вид: Y = f(X).

Функции f, включенные в парную регрессию в настоящем пакете, удовлетворяют двум основным условиям: они распространены в практике экономических исследований, каждое из уравнений регрессии путем преобразований типа логарифмирования и возведения в степень сводится к линейной модели.

Для реализации функции парной регрессии необходимо выбрать переменную Y (зависимая переменная), переменную Х (объясняющая переменная), а также сформировать список функций парной регрессии (табл.).

Для каждой функции параметры вычисляются по методу наименьших квадратов, а также рассчитывается критерий вида

,

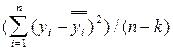где k – число оцениваемых параметров функции.

Та функция, которой соответствует минимальное значение критерия, считается оптимальной, и для нее рассчитываются все параметры.

Заметим, что с помощью коэффициентов регрессии нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различий единиц измерения и степени колебаний. Для устранения этого применяют: коэффициент эластичности; дельта-коэффициент; бета-коэффициент.

Как с помощью частных коэффициентов эластичности, так и с пoмощью бета-коэффициентов можно проранжировать факторы по степени их влияния на зависимую переменную, т.е. сопоставить их между собой по величине этого влияния. Вместе с тем нельзя непосредственно оценить долю влияния фактора в суммарном влиянии всех факторов. Для этой цели используются дельта-коэффициенты.

Для экономической интерпретации нелинейных, связей обычно пользуются коэффициентом элacтичнocти (табл.14.5.), который характеризует относительное изменение зависимой переменной при изменении объясняющей переменной на 1%.

Таблица 14.5. Основные функции парной регрессии

Модель	Преобразование	Матрицы
X	Y
Y=a+bX	Нет		-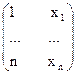
Y=a+bХ+cХХ	Нет		-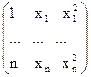
Y=a+b/Х	Нет		-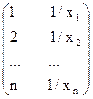
Y=1/(a+bХ)	Возведение в степень (-1)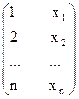
Y=1/(a+b*exp(-X))	Возведение в степень (-1)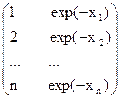
Y=a*exp(bX)	Логарифмирова-ние
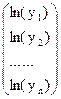
Y=a+b*ln(Х)	Нет		-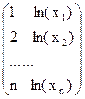
Y=	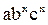Логарифмирова-ние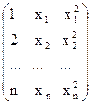
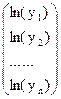
Y=	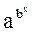Логарифмирова-ние
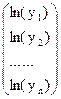
Модель	Преобразование	Матрицы
X	Y
Y=a+b/ln(x)	Нет		-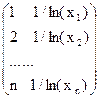
Y=	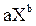Логарифмирова-ние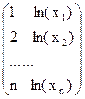
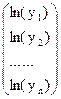
Y=a+bХ+c(Х)1/2	Нет		-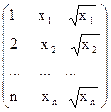
Y=Х/(a+bХ)	Нет
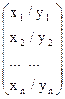
Y=a*exp(b/X)	Логарифмирова-ние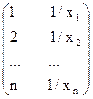
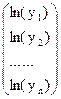
Y=	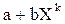Нет		-
Y=a+bX+cXX+…+dXk	Нет		-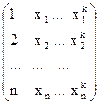

Если уравнение регрессии имеет вид у=f(x), то коэффициент эластичности рассчитывается как

,

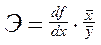где 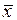- среднее значение переменной х; 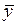- среднее значение переменной.

Производная берется в точке .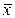

Таблица 14.6. Расчет коэффициентов эластичности

№п/п	Функция	Формула коэффициента эластичности
	Y=a+bx	Э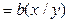
	Y=a+bx+cx2	Э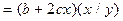
	Y=a+b/x	Э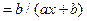
	Y=1/(a+bx)	Э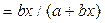
	Y=1/(a+b)e-x	Э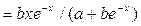
	Y=	Э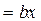
	Y=a+bln(x)	Э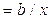
	Y=	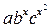Э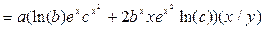
	Y=	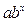Э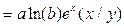
	Y=a+b/ln(x)	Э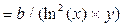
	Y=	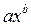Э=b
	Y=a+bx+c(x)1/2	Э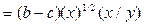
	Y=x/(a+bx)	Э=a/(a+bx)
	Y=	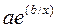Э=b/x
	Y=	Э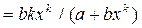
	Y=	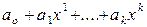Э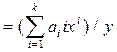

Дельта-коэффициент. Доля вклада каждого фактора в суммарное влияние составляет:

; ,

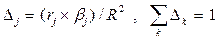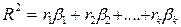где R² - коэффициент множественной детерминации; r_i - коэффициент парной корреляции между i –м фактором и зависимой переменной; β_i - β - коэффициент.

При корректно проводимом анализе величины дельта-коэффициентов
положительны, т.е. все коэффициенты регрессии имеют тот же знак, что и
соответствующие парные коэффициенты корреляции. Тем не менее, в случаях сильной коррелированности объясняющих переменных некоторые дельта-коэффициенты могут быть отрицательными вследствие того, что соответствующий коэффициент регрессии имеет знак, противоположный парному коэффициенту корреляции.

Бета-коэффициент. Для устранения различий в измерении и степени колеблемости факторов используется β коэффициент или коэффициент регрессии в стандартизованном виде:

,

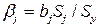где b_j - коэффициент регрессии при j -й переменной, S_j - оценка среднеквадратического отклонения j -й переменной, S_y - оценка среднеквадратического отклонения независимой переменной.

Он показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Факторный и компонентный анализ. Компонентный анализ является методом определения структурной зависимости между случайными переменными. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты Y₁,Y₂,...,Y_m получаются из исходных переменных X₁,X₂,...,X_m путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных X. При этом переменные Y₁,Y₂,...,Y_m некоррелированы между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений. Итак, i -я главная компонента Y_i:

.

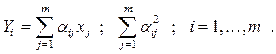
Пусть R - корреляционная матрица переменных X. Тогда - первый собственный вектор матрицы R. Кроме того, дисперсия первой главной компоненты равна первому собственному числу матрицы R, дисперсия второй главной компоненты равна второму собственному числу матрицы R и т.д.

Факторный анализ является более общим методом преобразования исходных переменных по сравнению с компонентным анализом. Модель факторного анализа имеет вид:

,

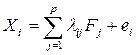где 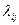- постоянные величины, называемые факторными нагрузками, F_j - общие факторы, используемые для представления всех р исходных переменных, e_i - специфические факторы, уникальные для каждой переменной, р 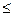m.

Задачами факторного анализа являются: определение числа общих факторов, определение оценок 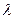, определение общих и специфических факторов. Для получения оценок общностей и факторных нагрузок используется эмпирический итеративный алгоритм, сходящийся к истинным оценкам параметров, суть которого сводится к следующему:

1⁰. Первоначальные оценки факторных нагрузок определяются с помощью метода главных факторов. На основании корреляционной матрицы R формально определяются оценки главных компонент:

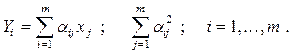
2⁰. Оценки общих факторов ищутся в виде:

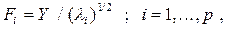
где 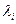- соответствующее собственное значение матрицы R.

3⁰. Оценками факторных нагрузок служат величины

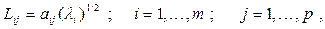
где a_ij - оценки 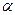_ij; L_ij – оценки 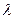_ij.

4⁰. Оценки общностей получаются как

.

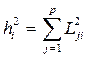5⁰. На следующей итерации модифицируется матрица R – вместо элементов главной диагонали подставляются оценки общностей, полученные на предыдущей итерации; на основании модифицированной матрицы R с помощью вычислительной схемы компонентного анализа повторяется расчет главных компонент (которые не являются таковыми с точки зрения компонентного анализа), ищутся оценки главных факторов, факторных нагрузок, общностей, специфичностей. Факторный анализ можно считать законченным, когда на двух соседних итерациях оценки общностей меняются слабо.

Преобразования матрицы R могут нарушать положительную определенность матрицы R и, как следствие, некоторые собственные значения R могут быть отрицательными. Для лучшей интерпретации полученных общих факторов к ним применяется процедура варимаксного вращения.

Если факторный анализ ведется в терминах главных компонент, то значения факторов могут быть вычислены непосредственно. Главные компоненты (без вращения) могут быть представлены в виде:

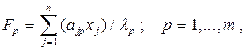
где a_jp - коэффициенты при общих факторах; 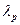- собственные значения; х_j - исходные данные (вектор-столбцы); F_p - главные компоненты (вектор-столбцы).

В случае вращения главных компонент соотношения, связывающие исходные переменные и значения факторов, несколько усложняются. Ниже в матричном виде приведено соотношение, оптимальное по скорости вычисления, а также независимое от метода вращения факторов:

,

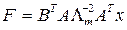где 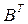- повернутая матрица А; А - матрица коэффициентов при общих факторах; 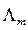- диагональная матрица m собственных членов; х - матрица исходных данных; F - матрица m повернутых факторов.

При определении числа общих факторов руководствуются следующими критериями: число существенных факторов можно оценить из содержательных соображений, в качестве р берется число собственных значений, больших либо равных единице (по умолчанию), выбирается число факторов, объясняющих определенную часть общей дисперсии или суммарной мощности.

Кластерный анализ. Классификация объектов по осмысленным группам, называемая кластеризацией, является важной процедурой в различных областях научных исследований. Кластерный анализ (КА) - это многомерная статистическая процедура, упорядочивающая исходные данные (объекты) в сравнительно однородные группы. Общим для всех исследований, использующих КА, являются пять основных процедур: 1) отбор выборки для кластеризации; 2) определение множества признаков, по которым будут оцениваться объекты в выборке; 3) вычисление значений той или иной меры сходства между объектами; 4) применение метода КА для создания групп исходных данных; 5) проверка достоверности результатов кластерного решения.

Каждый из перечисленных шагов играет существенную роль при использовании кластерного анализа в прикладном анализе данных. При этом 1, 2 и 5 шаги целиком зависят от решаемой задачи и должны определяться пользователем. Шаги 3 и 4 выполняются программой кластерного анализа.

В целом многие методы КА - довольно простые эвристические процедуры, которые не имеют, как правило, строгого статистического обоснования, но позволяют свести к минимуму вероятность допущения ошибки при трактовке результатов КА.

Разные кластерные методы могут порождать различные решения для одних и тех же данных. Это обычное явление в большинстве прикладных исследований. Окончательным критерием считают удовлетворенность исследователя результатами КА.

Разработанные кластерные методы образуют семь основных семейств: иерархические агломеративные методы; иерархические дивизимные методы; итеративные методы группировки; методы поиска модальных значений плотности; факторные методы; методы сгущений; методы, использующие теорию графов. По данным ряда исследований, около 2/3 приложений КА используют иерархические агломеративные методы.

Процесс кластеризации начинается с поиска двух самых близких объектов в матрице расстояний. На последующих шагах к этой группе присоединяется объект, наиболее близкий к одному из уже находящихся в группе. По окончанию процесса все объекты объединены в один кластер.

Отметим несколько важных особенностей иерархических агломеративных методов. Во-первых, все эти методы просматривают матрицу расстояний размерностью 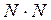(где N - число объектов) и последовательно объединяют наиболее схожие объекты. Именно поэтому они называются агломеративными (объединяющими). Во-вторых, последовательность объединения кластеров можно представить визуально в виде древовидной диаграммы, часто называемой дендрограммой. В-третьих, для понимания этого класса методов не нужны обширные знания матричной алгебры или математической статистики. Вместо этого дается правило объединения объектов в кластеры. Например, в системе СтатЭксперт разработана программа кластерного анализа, основанная на иерархической агломеративной процедуре и позволяющая пользователю управлять процессом кластеризации. Кратко поясним суть предлагаемого метода.

Вначале ищутся два наиболее близких объекта (предположим, А и В). Предположим, что расстояние между объектами А и В равно R. В один кластер объединяются объекты, расстояние между которыми меньше, чем (10-С)R, где С - четкость классификации, параметр управления процессом, принимающий значения от 1 до 10, который может меняться пользователем. При C=10 на каждом шаге объединяются только два самых близких элемента, т.е. имеет место иерархическая агломеративная процедура в чистом виде. Однако, как показывает практика использования КА, пользователю важнее выделить в пространстве группы объектов с разной плотностью. В этом случае величину С необходимо уменьшать. Минимальное расстояние R пересчитывается на каждом шаге кластерного анализа.

Объединение. На каждом шаге кластерного анализа происходит объединение объектов, т.е. из нескольких объектов образуется один кластер. Процедура кластеризации заканчивается тогда, когда все первичные объекты исчерпаны Допустим, на каждом шаге объединяются n объектов. Из этих объектов образуется один кластер как центр тяжести этих объектов (среднее арифметическое по каждой координате).

Размерность задачи уменьшается на величину n-1 (n объектов удаляются, один добавляется). Далее производится пересчет матрицы расстояний.

В программе реализован кластерный анализ наблюдений, т.е. в результате вычислительной процедуры каждое наблюдение относится к той или иной группе. Кластеризация проводится на основе одной из двух метрик:

евклидово расстояние: ;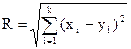

корреляционное расстояние: ,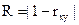

где х={x₁, x₂, …, x_k} и у={y₁, y₂, …, y_k} - две точки; r_xy - парный коэффициент корреляции между x и y.

В программе реализованы три метода классификации: метод "ближайшего соседа", метод "ОЛИМП", метод "К-средних".

Метод ближайшего соседа является представителем: иерархических агломеративных методов, которые используют приблизительно 2/3 приложений КА. В этом методе процесс кластеризации начинается с поиска двух самых близких объектов в матрице расстояний. На последующих шагах к этой группе присоединяется объект, наиболее близкий к одному из уже находящихся в группе. По окончании кластеризации все объекты объединены в один кластер.

Метод "ОЛИМП" основан на иерархической агломеративной процедуре. На каждом шаге кластерного анализа происходит объединение объектов, т.е. из нескольких объектов образуется один кластер. Процедура кластеризации заканчивается тогда, когда все первичные объекты исчерпаны Допустим, на каждом шаге объединяются п объектов. Из этих объектов образуется один кластер как центр тяжести этих объектов (среднее арифметическое по каждой координате). Размерность задачи уменьшается на величину (n-1), так как n объектов удаляются, а один добавляется. Далее производится пересчет матрицы расстояний.

Метод К-средних относится к итеративным методам группировки. Его достоинством является возможность управления количеством групп (К-групп), на которые должны бытъ разнесены наблюдения. Алгоритм метода состоит в следующем:

1°. Начать с исходного разбиения данных не некоторое заданное число кластеров; вычислить центры тяжести этих кластеров (в программе исходное разбиение выполняется методом ближайшего соседа)..

2°. Поместить каждую точку данных в кластер с ближайшим центром тяжести.

3°. Вычислить новые центры тяжести кластеров; кластеры не заменяются на новые до тех пор, пока не будут просмотрены полностью все данные. Шаги 2 и 3 повторяются до тех пор, пока не перестанут меняться кластеры.

Содержательно этот метод направлен на поиск разбиения выборки с минимальным разбросом. В отличие от иерархических агломеративных методов, которые требуют вычисления и ранения матрицы сходств между объектами размерностью N • N, итеративные методы работают непосредственно с первичными данными. Поэтому с их помощью возможно обрабатывать довольно большие множества данных Более того, итеративные методы делают несколько просмотров данных и могут компенсировать последствия плохого исходного разбиения данных, тем самым устраняя самый главный недостаток иерархических агломеративных методов. Эти методы порождают кластеры одного ранга, которые не являются вложенными, и поэтому не могут быть частью иерархии. Большинство итеративных методов не допускают перекрытия кластеров.

На результаты кластеризации существенное влияние оказывает выбор меры расстояния или меры несходства. В программе кластеризация проводится на основе одной из четырех метрик: евклидово расстояние; корреляционное расстояние; расстояние городских кварталов (Манхеттенское); расстояние Махаланобиса (обобщенное расстояние), вычисляемых по формулам табл.14.7.

Таблица 14.7. Расчетные формулы метрик кластеризации

№	Показатели	Формулы расчета*
1.	Евклидово расстояние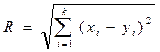
2.	Корреляционное расстояние
3.	Расстояние городских кварталов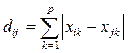
4.	Расстояние Махаланобиса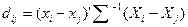

* - в табл.14.7. введены следующие обозначения: для пп.1 и 2 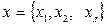и - две точки; r_xy - парный коэффициент корреляции между х и у; для пп. 3 и 4 где 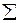- общая внутригрупповая дисперсионно-ковариационная матрица, а Х_i, Х_j - векторы значений переменных для объектов i и j.

Главным недостатком коэффициента корреляции как меры сходства является его чувствительность к форме при сниженной чувствительности к величине различий между переменными. Он также часто не удовлетворяет неравенству треугольника, и корреляция, вычисленная этим способом, не имеет статистического смысла, так как среднее значение определяется по совокупности всевозможных разнотипных переменных, а не по совокупности объектов (смысл "среднего" по разнотипным переменным далеко не ясен). Однако данный коэффициент широко используется в приложениях кластерного анализа.

Несмотря на важность евклидовой и других метрик, они имеют серьезные недостатки. Наиболее важный состоит в том, что оценка сходства сильно зависит от различий в сдвигах данных. Переменные, у которых одновременно велики абсолютные значения и стандартные отклонения, могут подавить влияние переменных с меньшими абсолютными размерами и стандартными отклонениями. Более того, метрические расстояния изменяются под воздействием преобразованной шкалы измерения переменных, при которых не сохраняется ранжирование по евклидову расстоянию. Чтобы уменьшить влияние относительных величин переменных, обычно перед вычислением расстояния переменные нормируют к единичной дисперсии и нулевому среднему.

В отличие от евклидовой и других аналогичных метрик, метрика расстояния Махаланобиса с помощью матрицы дисперсий-ковариаций связана с корреляциями переменных. Когда корреляция между переменными равна нулю, расстояние Махаланобиса эквивалентно квадратичному евклидову расстоянию.

Для графической интерпретации результатов кластерного анализа приводится график расположения исходных объектов в пространстве первых двух главных компонент. При этом объекты, попавшие в один кластер, отображаются одним цветом. Иногда объекты из разных кластеров расположены столь близко, что может создаться иллюзия о неправильной классификации. Это связано с тем, что классификация проводится по большому числу переменных, а график строится по двум координатам, хотя и отражающим основные особенности данных, поэтому расхождения между результатом классификации и графическим отображением неизбежна.

Частотный анализ. Вместе с долговременными изменениями во временных рядах часто появляются некоторые регулярные колебания, изменения наблюдаемых значений которых могут быть строго периодическими или близкими к таковым, оцениваясь в частотном аспекте. Для выявления наличия и устойчивости периода этих колебаний обычно используется математический аппарат частотного анализа: гармонический анализ, спектральный анализ, частотная фильтрация, кросс-спектральный анализ, который в совокупности позволяет с разных позиций анализировать исследуемый показатель, но он эффективен лишь при достаточно большом объеме данных: желательно иметь 200-300 наблюдений, но не менее 50 наблюдений, из которых предварительно исключена тенденция (за исключением методов частотной фильтрации).

При гармонический анализе временной ряд наблюдений представляется линейными комбинациями функций sint - cost, на основании конечного преобразования Фурье с выявлением наиболее существенных гармоник. Если Y(t) - временной ряд t=1,2...T, то имеем:

,

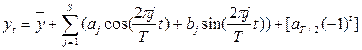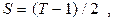
где 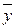- оценка математического ожидания ряда Y(t), а последнее слагаемое добавляется в том случае, когда Т - четное число.

Коэффициенты a_j, b_j, a_T/2 вычисляются как

; ; .

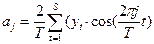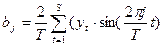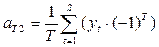Итак, временной ряд можно представить в виде суммы гармоник, при этом мощность каждой из них определяется как 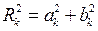, а k - я гармоника считается статистически значимой, если она вносит существенный вклад в дисперсию временного ряда, (т.е. если отвергается статистическая гипотеза о том, что R_k=0). Для проверки гипотезы вычисляется критерий вида

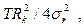
где 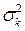- оценка дисперсии отклонения вычисляемых значений от фактических.

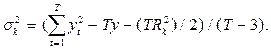
Вычисляемая величина имеет F -распределение с v₁= 2 и v₂ = Т- 3 степенями свободы. Гипотеза отвергается (гармоника считается значимой), если вычисленная величина больше, чем 95% точка F-распределения с соответствующими степенями свободы.

При спектральном анализе периодограмму x(t), t=0,l,...,Т временного ряда можно рассчитать как

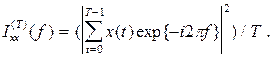
Если исходные данные квантованы с интервалом 1 и частотой Найквиста, для них равной 0.5, то периодограмма и спектральная плотность рассчитывается на интервале от 0 до 0,5 в точках f(j)=j/2M, j=0,1,...M.

Спектральную плотность можно определить по оценке Бартлетта, являющейся усреднением периодограмм, вычисленных по непересекающимся отрезкам временных рядов. Пусть имеем:

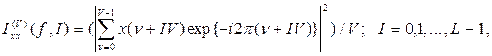
где V – ширина временного интервала; I – номер интервала; S - смещение текущего временного интервала относительно предыдущего.

Тогда оценка спектральной плотности получается как

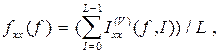
Спектральные оценки можно сглаживать при помощи "окон", обеспечивающих уменьшение дисперсии выборочной спектральной плотности. На практике из множества известных окон обычно используются: а) прямоугольное окно вида: 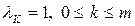; б) окно Тьюки-Хеннинга вида 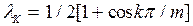; в) окно Парзена следующего вида

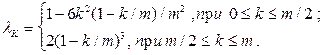
Параметры, необходимые для расчета спектра мощности, рассчитываются по следующему алгоритму: 1) вычисляют значение V: V=n/3 (n - число наблюдений); если V<10, то принимают V=10; если V>50, то принимают V=50; 2) определяют величину смещения: S=V/2.

При кросс-спектральноманализе оценивается связь между частотными составляющими двух временных рядов на основе параметров когерентности, фазового сдвига и коэффициента усиления (табл.14.8).

№	Показатели	Формулы расчета
1.	Взаимные коариационные функции	;
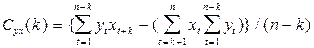
2.	Ко-спектр (действительная часть спектра)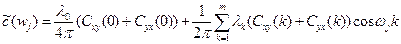
3.	Квадратурный спектр (мнимая часть спектра)	;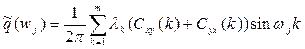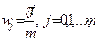
4.	Когерентность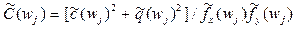
5.	Фазовый сдвиг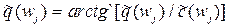
6.	Коэффициент усиления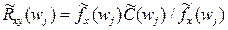
7.	Спектр для ряда х

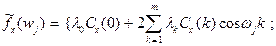
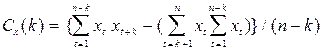
Tаблица 14.8. Расчетные параметра кросс-спектрального анализа

Аналогично спектру можно получить оценку спектра 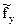для ряда y. Интепретация результатов кросс-спектрального анализа – тонкий процесс. Например, когерентность аналогична квадрату коэффициента корреляции на соответствующей частоте, коэффициент усиления – коэффициенту линейной регрессии процесса по процессу на соответствующей частоте, фазовый сдвиг характеризует временное смещение между составляющими двух процессов.

При частотной фильтрации, осуществляемой посредством высокочастотного (ВУФ) и низкочастотного (НУФ) фильтра, для каждого из них рассчитывается соответствующая силовая и фазовая характеристики (табл.14.9). Низкочастотный фильтр предназначен для устранения тренда (низкочастотной составляющей временного ряда наблюдений). Высокочастотный фильтр, наоборот, предназначен для выделения тренда из исходных данных.

Таблица 14.9. Расчетные формулы параметров фильтров

№	Показатели	Расчетные формулы*
1.	Выход НУФ	; ; ; ;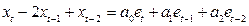
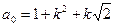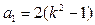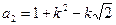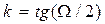
2.	Выход ВУФ	; ; ; ;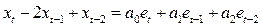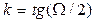

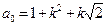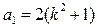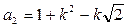
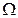- - частота отсечки; е_t – оценка ВЧ(НЧ) составляющей для НУФ(ВУФ), при их оценке теряются два первых наблюдения. Оценкой тренда в этом случае является ряд 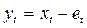, который может быть использован для прогнозирования.