Линейные модели временных рядов

Модель авторегрессии. В модели авторегрессии АР(р) порядка "р" текущий уровень ряда представляется в виде взвешенной суммы "р" предыдущих наблюдений:

X(t) = a₁X(t – 1) + a₂X(t – 2) + … +a_pX(t – p).

Параметры модели могут быть оценены по МНК (простая авторегрессия) или иным методом (как в методе Бокса-Дженкинса). Порядок авторегрессии (величина "р ") определяется путем перебора, а его начальная оценка формируется на основе анализа автокорреляционной функции. Лучшей считается величина, при которой достигнута наименьшая дисперсия ошибок.

В сезонной модели авторегрессии АР(р) порядок выбирается равной периоду сезонности (колебаний). Во многих случаях сезонная АР (р) - модель с оценками по МНК оказывается "перегруженной" незначимыми коэффициентами, и вследствие этого она обычно уступает аналогичной модели Бокса-Дженкинса Для повышения устойчивости модели в большинстве случаев целесообразно строить ее для стационарного процесса, т.е. ряда с исключенной тенденцией.

Метод Бокса-Дженкинса. Если временной ряд стационарный (есть наличие статистического равновесия относительно постоянной средней), его можно представить широким классом линейных моделей, называемых модулями авторегрессии-скользящего среднего (АРОС). Это значит, что:

.

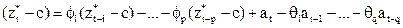где 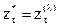- значения предварительно преобразованной переменной; a_t -процесс "белого шума"; 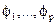- параметры авторегрессии; 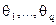- параметры скользящего среднего.

Если использовать оператор сдвига назад В, т.е. B_z = z_t-1, то АРCС-модель можно записать в операторной форме:

.

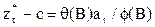Параметры этой модели должны удовлетворять следующим условиям: а) для стационарности корни уравнения ф(В) = 0 должны лежать вне единичного круга для оператора авторегрессии ф(В) (ряда находятся в статистическом равновесии относительно фиксированного среднего); б) для обеспечения обратимости корни уравнения q (В) = 0 должны должны лежать вне единичного круга для оператора скользящего среднего q (В).

Чтобы добиться экономии параметров, в модель включают одновременно операторы авторегрессии и скользящего среднего.

В целом авторегрессионные модели и модели скользящего среднего модели известны относительно давно, но их использование в моделировании временных рядов затруднялось из-за отсутствия соответствующих методов идентификации, оценивания и контроля этих моделей, наличия неадекватных методов для описания нестационарных рядов.

При формализации нестационарных рядов используют такие классы моделей, которые пригодны для представления широкого диапазона практических ситуации, т.е. используют конечные разности порядка d:

.

Конечная разность первого порядка имеет вид .

Стационарный ряд можно затем представить с помощью АРСС-модели:

w_t – c = q(B)a_t / j(B).

Определенная выше модель называется авторегрессионной интегрированной моделью скользящего среднего или АРИСC(p,d,q). Взаимосвязанная статистическая методика метода Бокса-Дженкинса включает в себя: а) идентификацию временного ряда (т.е. определение размерностей операторов конечной разности, авторегрессии и скользящего среднего); б) оценивание параметров модели; в) проверку адекватности модели.

Сезонная модель Бокса-Дженкинса содержит сезонные операторы конечной разности, авторегрессии и скользящего среднего. В операторном виде она приобретает вид:

,

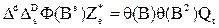где S - период сезонности, - оператор сезонной конечной разности,

,

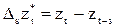где D - порядок сезонной конечной разности, Ф - оператор сезонной авторегрессии порядка Р, q - сезонного скользящего среднего порядка Q, d, ф, Q - определены выше.

Модель называется сезонной моделью авторегрессии-скользящего среднего (р, d, q) x (P, D, Q). Основные этапы разработки сезонной модели аналогичны этапам для несезонной модели.

Метод ОЛИМП. Этот метод является распространением моделей авторегрессии скользящего среднего для моделирования нестационарных временных рядов.

Формально модель ОЛИМП соответствуют модели АРСС(р, q), за исключением того, что на вход модели поступает нестационарный, вообще говоря, временной ряд. Так же, как для и несезонных моделей, сезонная модель ОЛИМП отличается от авторегрессионных моделей тем, ^то на ее вход могут поступать нестационарные временные ряды, которые не приводятся к стационарным путем взятия конечных разностей. В операторном виде модель ОЛИМП (р,q)х(Р,Q) имеет вид:

.

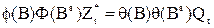С точки зрения общих соображений размерности операторов авторегрессии для модели ОЛИМП должны быть несколько больше, чем для модели Бокса-Дженкинса при моделировании одинаковых временных рядов.

Если идентифицирована модель Бокса-Дженкинса с параметрами р, d, q, то соответствующая модель ОЛИМП должна иметь параметры р'=р+d.

Если процесс удовлетворяет стохастическому разностному уравнению порядка p (авторегрессионный процесс)

,

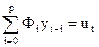где Ф_i - коэффициенты оператора авторегрессии, u_t - последовательность независимых одинаково распределенных случайных величин с дисперсией 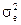, t = 1, 2, …, T.

Если известны начальные значения у-р, у -р+1,...,у-1, то прогноз имеет вид:

,

где Е - оператор математического ожидания, будет иметь наименьшую дисперсию вне зависимости от значения корней характеристического уравнения.

Сравнительные характеристики двух подходов к моделированию авторегрессионных процессов приведены в табл. 14.4.

Таблица 14.4. Методы моделирования авторегрессионных процессов

Характеристики	Известная схема	Новая схема
Тип моделируемых процессов	Стационарные	Стационарные и нестационарные
Исходные предпосылки	Остатки независимы и одинаково распределены	Остатки независимы, одинаково распределены, заданы начальные условия
Базовое представление наблюдений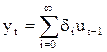
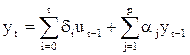
Ограничения	Корни характеристического уравнения вне единичного круга	Нет ограничений
Вид прогноза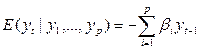

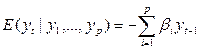
В целом статистические оценки модели являются состоятельными вне зависимости от значения корней характеристического уравнения. В практическом плане свойства состоятельности оценок оказываются вполне достаточны для их использования.

Оценка качества моделей. Проведем оценку качества модели по критериями точности и адекватности.

Схема формирования интегрированных критериев точности и адекватности, а также общего критерия качества прогнозирования состоит в следующем. С помощью механизма параметров пакета формируется состав отдельных критериев, на основе которых рассчитывается интегрированный показатель (так, точность можно характеризовать только коэффициентом детерминации, или дисперсией и средней ошибкой аппроксимации, или всеми тремя перечисленными выше критериями точности).

Предварительно для каждого отдельного критерия разрабатывается процедура его нормировки. Нормированный критерий получается из исходной статистики критерия таким образом, чтобы выполнялись условия: нормированный критерий равен 100, если модель абсолютно точная (адекватная); нормированный критерий равен 0, если модель абсолютно неточная (неадекватная).

Обобщенный критерий качества модели формируется как взвешенная сумма обобщенного критерия точности (его вес 0.75) и обобщенного критерия адекватности (его вес 0.25), т.е. точностным характеристикам придается большой вес. В качестве представителя характеристик точности используется нормированное значение средней относительной ошибки аппроксимации, а в качестве представителя критериев адекватности -нормированное значение критерия Дарбина-Уотсона и характеристики нормального закона распределения остаточной компоненты Числовое значение обобщенного критерия качества лежит в диапазоне от 0 до 100 (минимум соответствует абсолютно плохой модели, а максимум - идеально отображающей развитие показателя). Опыт применения этого показателя показывает, что достаточно надежными являются модели, имеющие оценку качества не менее 75.

Так как формально-статистический выбор лучшей модели во многих случаях не дает полной уверенности в его правильности, то, кроме указанной программой модели, целесообразно просматривать результаты прогнозирования других моделей, имеющих близкое значение критерия качества Адекватными моделями считаются такие, у которых остаточная компонента имеет свойства независимости, случайности и нормальности распределения.

Критерий Дарбина-Уотсона является наиболее распространенным критерием для проверки корреляции внутри ряда. Если величина Д

,

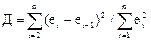где e_i - расхождение между фактическими и расчетными уровнями, имеет значение, близкое к 2, то можно считать модель регрессии достаточно адекватной.

Для построения интервального прогноза необходимо выполнение свойства нормальности распределения остаточной компоненты, оцениваемого на основе коэффициентов асимметрии и эксцесса.

При оценке адекватности уравнения регрессии учитывается также корреляционное отношение, которое характеризует долю дисперсии, зависимой переменной, объясняемой уравнением регрессии. Корреляционное отношение рассчитывается по формуле

,

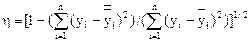где 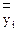- расчетные значения зависимой переменной, 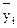- среднее значение.

Точность модели характеризует близость расчетных наблюдений фактическим на периоде аппроксимации. Считается, что модели с меньшим расхождением между фактическими и расчетными значениями отражают исследуемый процесс. Для характеристики степени близости используются величины: среднее квадратическое отклонение (или дисперсии), учитывающее сложность модели; коэффициент детерминации (чем ближе к 1, тем более точнее модель); средняя относительная ошибка аппроксимации (чем ближе к 0, тем точнее модель); среднее значение (должно быть близко к нулю); максимальное отклонение.

Статистически точность прогнозов можно оценить, только используя ретропрогноз. Его суть состоит в построении модели по усеченному объему данных (N-k) точек с последующим сравнением прогнозных оценок с известными фактическими, но умышленно «забытыми» k уровнями ряда). По результатам сравнения вычисляются следующие показатели точности: среднее значение; среднеквадратическое отклонение; средний модуль ошибок прогнозирования (%); максимальное и минимальное отклонение. Чем меньше значение этих величин, тем выше качество ретропрогноза. Данный подход дает хорошие результаты, если на периоде ретропрогноза не содержится принципиально новых закономерностей.

Построение обобщенного прогноза. На практике часто встречается ситуация, когда несколько моделей могут быть адекватными, с малыми различиями между их характеристиками. В этом случае целесообразно строить обобщенный прогноз, формируемый как линейная комбинация частных прогнозов:

,

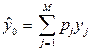где М - число объединяемых прогнозов; 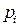. - весовые коэффициенты частных прогнозов; 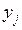- частные прогнозы.

Весовые коэффициенты определяются из условия минимума дисперсии ошибок обобщающего прогноза (максимума его точности), которая находится как сумма всех элементов ковариационной матрицы ошибок частных прогнозов с соответствующими весами:

;

,

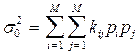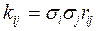где k_ij - корреляционный момент, характеризующий совместно распределение ошибок i и j - частных прогнозов: 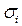и - средние квадратичные ошибки; r_ij - коэффициент корреляции между рядами ошибок частных прогнозов y_{i И} y_j.

Сумма весовых коэффициентов должна давать единицу (это необходимое условие того, чтобы дисперсия обобщающего прогноза не превышала дисперсии частных прогнозов. Ковариационная матрица ошибок частных прогнозов в этом случае будет иметь вид:

,

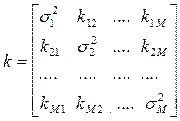а дисперсия обобщающего прогноза соответствует сумме всех элементов матрицы:

.

В точке минимума функции все (М-1) первые частные производные должны обращаться в нуль.

Приравняв к нулю все (М-1) первые частные производные по переменным р₁,р₂,…р_М-1, получаем систему (М-1) линейных уравнений с (М-1) неизвестными:

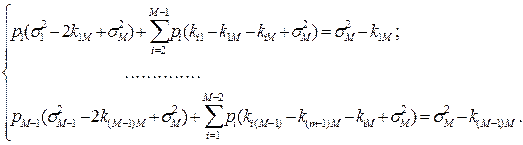
Коэффициенты при переменных составят матрицу В, элементы которой определяются как

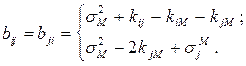
Вектор свободных членов будет состоять из элементов с_j:

.

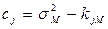Такую систему уравнений можно решить с помощью линейной алгебры.

Алгоритм объединения частных прогнозов состоит в следующем:

1⁰. Вычисляются дисперсии ошибок частных прогнозов и строится ковариационная матрица:

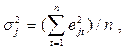
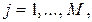
где е_j - ошибки частных прогнозов; t -порядковый номер наблюдения, t = 1,…,n.

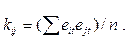
2⁰. Строятся матрица В и вектор С по формулам

;

.

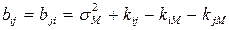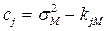3⁰. Из решения системы линейных уравнений определяется (М-1) значение р_j, при этом весовой коэффициент р_М определяется как

.

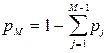4⁰. Производится проверка условия:

p_j>0, j=1,…,M, при этом:

а) eсли условие не выполняется, прогнозы у_j исключаются и производится перерасчет весовых коэффициентов (с возвратом к пункту 2⁰);

б) eсли все весовые коэффициенты положительны, то вычисляется значение обобщающего прогноза y_o и коэффициент условной эффективности :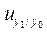

; ,

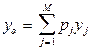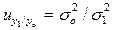где 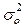- дисперсия ошибок комплексного прогноза; 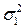- дисперсия ошибок наилучшего частного прогноза.

5⁰. Так как в большинстве случаев точность прогнозов изменяется во времени, формулы оценки весовых коэффициентов модифицируются так, что более поздним ошибкам присваивается большее значение; этим производится корректировка обобщающего прогноза путем изменения весовых коэффициентов в сторону наилучшего частного прогноза :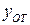

,

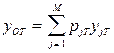где p_jT - весовой коэффициент частного прогноза в момент времени Т; y_jT - частный прогноз в момент времени Т; 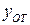- обобщенный прогноз в момент времени Т.

Для повышения стабильности динамики изменения весов в алгоритме их корректировки можно использовать схему экспоненциального сглаживания.

В целом для проведения обобщения необходимо иметь не менее двух адекватных моделей, а для повышения устойчивости результатов количество обобщаемых частных прогнозов не должно превышать пяти.