Высшего профессионального образования 3 страница

Тор образуется, если окружность вращается вокруг оси, которая не проходит через ее центр, но принадлежит плоскости окружности. Если окружность не пересекает ось вращения, то тор называется кольцом. Тор является поверхностью четвертого порядка. Уравнение тора с центром в начале координат имеет вид:

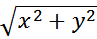( – а)² + z² = r².

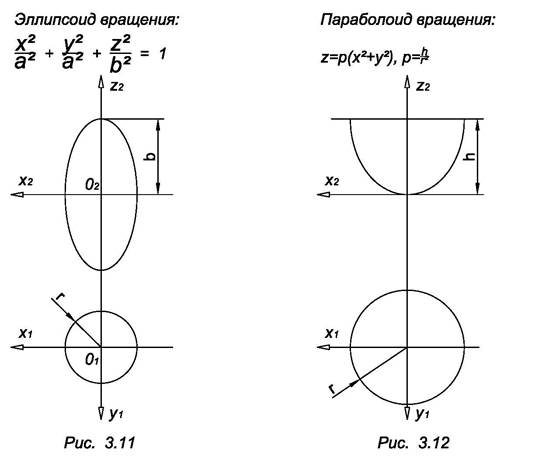
3. Поверхности вращения второго порядка образуются вращением кривых второго порядка вокруг их осей (рис. 3.11, 3.12). К ним относятся также поверхности, образованные вращением прямой линии.

3.5 Линейчатые поверхности

Линейчатую поверхность можно рассматривать как непрерывное множество последовательных положений движущейся по определенному закону прямой линии (образующей). Однополостный гиперболоид, цилиндр и конус вращения тоже относятся к линейчатым поверхностям.

В общем случае закон движения образующей может быть задан тремя криволинейными направляющими, которые пересекает любая образующая линейчатой поверхности.

Пусть линейчатая поверхность задана тремя направляющими p, g, f. Выберем на направляющей p произвольную точку А (рис. 3.13). Тогда точка А и направляющая g определяет некоторую коническую поверхность Ф, Ф П f =К. Точки К и А определяют прямолинейную образующую поверхности, заданной тремя криволинейными направляющими. Аналогично строятся и др. образующие линейчатой поверхности.

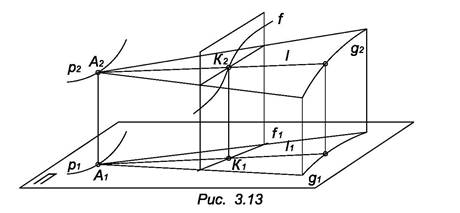
Если в качестве направляющих выбрать три скрещивающиеся прямые, не параллельные одной плоскости, то образующая поверхности при непрерывном движении опишет однополостный гиперболоид.

Прямолинейная направляющая может быть несобственной (бесконечно удаленной) прямой, тогда она задается плоскостью, которая называется плоскостью параллелизма.

Линейчатые поверхности с плоскостью параллелизма может быть образована движением образующей по двум направляющим при условии, что все образующие параллельны неподвижной плоскости (плоскости параллелизма).

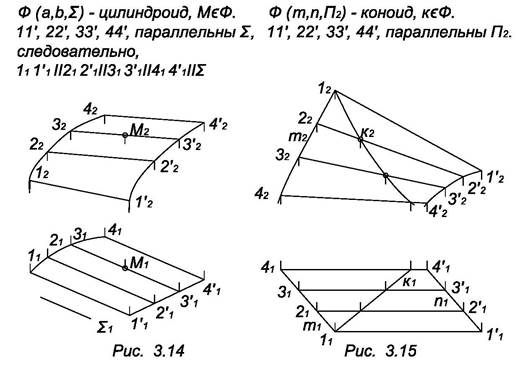
В зависимости от формы направляющих поверхности с плоскостью параллелизма называются: цилиндроидом, когда обе направляющие – кривые (рис. 3.14); коноидом, когда одна направляющая кривая, а другая прямая (рис. 3.15); гиперболическим параболоидом (косой плоскостью), когда направляющие – скрещивающиеся прямые (рис. 3.16). Геометрическая часть определителя таких поверхностей содержит направляющие и плоскость параллелизма.

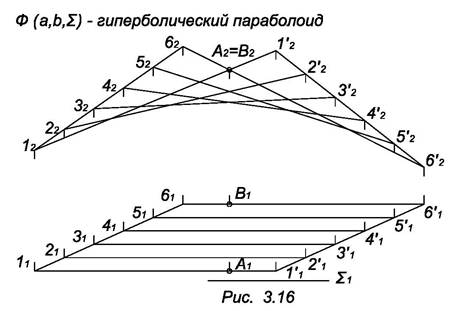
На рис. 3.16 изображен отсек (часть) поверхности. Для определения видимости очерковых образующих 11^’ и 65^’ выбраны конкурирующие точки А и В. Очерковая линия n строится как огибающая фронтальных проекций прямолинейных образующих. Гиперболический параболоид (косая плоскость) относится также к классу поверхностей второго порядка.

Взаимным пересечением образующих косая плоскость разбивается на отдельные, почти «плоские» части, по контуру которых могут быть легко изготовлены и собраны различные оболочки.

Развертывающиеся линейчатые поверхности имеют в своем определителе одну криволинейную направляющую.

Торс образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой (направляющей), называемой ребром возврата.

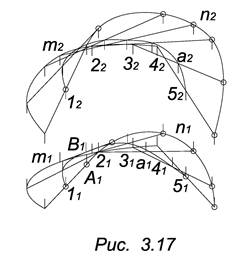Торс вполне определяется заданием направляющей. Торс состоит из двух частей, разграниченных по ребру возврата. Ф (а) – торс. Линии m и n принадлежат Ф (рис. 3.17).

Коническую и цилиндрическую поверхности можно рассматривать как частные случаи поверхности торса, когда ее ребро возврата вырождается в точку.

Коническая поверхность образуется движением прямолинейной образующей l, которая пересекает некоторую кривую линию а (направляющую) и проходит через неподвижную точку S (вершину). Ф (а, S) – коническая поверхность (рис. 3.18). Точка М € Ф.

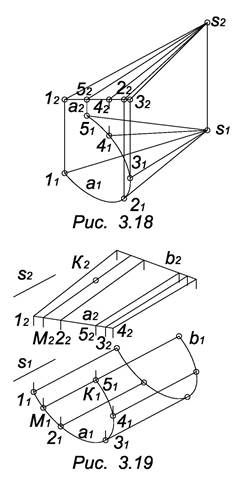Цилиндрическая поверхность образуется движением прямолинейной образующей l, которая пересекает некоторую кривую линию а (направляющую) и параллельна данной прямой s (рис. 3.19). Ф (а, S) – цилиндрическая поверхность. Линия b € Ф. Видимость на горизонтальной проекции определена с помощью конкурирующих точек К и 5.

Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности, у которой вершиной является бесконечно удаленная точка данной прямой s.

3.6 Уравнение линейчатой поверхности

Пусть направляющие линейчатой поверхности p, f, g заданы системой уравнений:

z₁ = f₁ (x₁) z₂ = f₂ (x₂) z₃ = f₃ (x₃)

y₁ = u₁ (x₁) y₂ = u₂ (x₂) y₃ = u₃ (x₃)

Уравнение прямой, проходящей через две точки:

= =

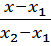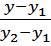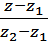
Образующая поверхности должна проходить через точки, принадлежащие данным направляющим, следовательно, в уравнении прямой необходимо подставить значения z₁, y₁, z₂, y₂, полученные из уравнения направляющих p и f.

- - ;

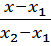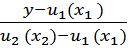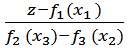И значения z₁, y₁, z₃, y₃ из уравнений направляющих p и g.

- - .

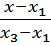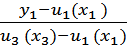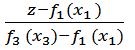Исключая из полученных четырех уравнений x₁, x₂ и x₃ получим уравнение искомой поверхности.

Пример 1. Составить уравнение косой плоскости, направляющие которой

z₁ = px₁ + g z₂ = ky₂

y₁ = 0 x₂ = 0

и плоскость параллелизма z = 0 (рис. 3.20).

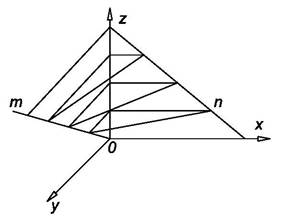Из условия параллельности прямой (образующей) плоскости Оxy следует, что

z₁ = z₂ = z, и очевидно, что

x₁ = 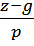, y₂ = ,

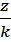Подставляя эти значения в уравнения прямой, получим

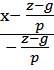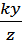= = или z² – pxz – kyz + kgy – gz = 0

Исследовать это уравнение предлагается самостоятельно.

3.7 Поверхности второго порядка

Поверхность второго порядка можно определить либо как поверхность, пересекающуюся с произвольной плоскостью по кривой второго порядка (действительной, мнимой или распавшейся на две прямые), либо как поверхность, пересекаемую произвольной прямой, не принадлежащей ей, в двух точках (действительных различных, действительных совпавших, мнимых).

Мы уже познакомились с некоторыми поверхностями второго порядка, которые называют еще квадриками.

1. Конические и цилиндрические поверхности являются поверхностями второго порядка, если их направляющие являются кривыми второго порядка.

Такие поверхности называют еще линейчатыми квадриками.

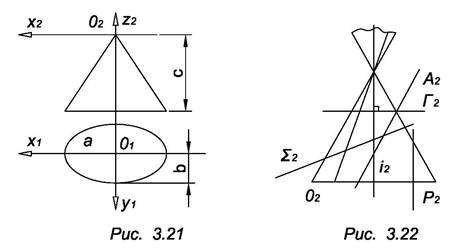
Если направляющей конической поверхности является эллипс, то поверхность называется эллиптическим конусом (рис. 3.21). Уравнение эллиптического конуса, вершина которого находится в начале координат, имеет вид:

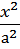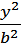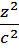+ - = 0, при а = b это уравнение конуса вращения.

Эллиптический конус и конус вращения занимают особое место среди поверхностей второго порядка, они примечательны тем, что их поверхности содержат все виды кривых второго порядка. К числу второго порядка относятся две прямые (различные или совпавшие). В проективной геометрии принято считать, что прямая содержит одну бесконечно удаленную точку и две параллельные прямые пересекаются в бесконечно удаленной точке. Эллипс и окружность не имеют бесконечно удаленных точек, парабола имеет одну такую точку, а гипербола – две.

На рис. 3.22 задана фронтальная проекция конуса вращения Ф. Плоскость Г пересекает его по окружности, плоскость ∑ - по эллипсу; Л параллельна одной образующей, следовательно, линия пересечения Л и Ф имеет одну бесконечно удаленную точку, т.е. является параболой; P параллельна двум образующим, значит, линия пересечения P и Ф имеет две бесконечно удаленные точки, т.е. является гиперболой; О проходит через вершину конуса, т.е. пересекает конус по двум прямым.

Вместо термина кривая второго порядка применяется также термин коническое сечение или коника.

2. Трехосный эллипсоид:

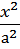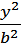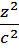+ + = 1

Ф (е, g) – эллипсоид.

Трехосный эллипсоид может быть задан проекциями очерковых линий. Его горизонталями являются эллипсы, которые подобны горизонтальному очерку (рис. 3.23).

Эллипсоид вращения и сфера являются частными случаями трехосного эллипсоида (см. рис. 3.10 и 3.11).

3. Эллиптический параболоид:

Z = +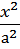

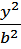
Ф (е, g) – эллиптический параболоид (рис. 3.24).

Горизонталями этой поверхности являются эллипсы, подобные эллипсу е. Их горизонтальные проекции подобны и подобно расположены, т.е. гомотетичны. Центром гомотетии является точка О₁. Исходя из этого строится горизонтальная проекция параллели К. если известна К₂. Очевидно, /О₁С₁/ - большая полуось искомого эллипса. Чтобы построить его малую полуось необходимо провести С₁D₁ ║ А₁В₁, как показано на рис. 3.24.

Параболоид вращения является частным случаем эллиптического параболоида.

Гиперболический параболоид рассмотрен в разделе линейчатые поверхности.

4. Однополостный и двуполостный гиперболоиды:

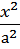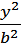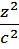+ - = 1

Ф (е, g) – однополостный эллиптический гиперболоид (рис. 3.25). М € Ф.

Частный случай однополостный гиперболоид вращения

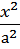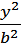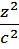- - + = 1

Ф (е, g) – двуполостный эллиптический гиперболоид (рис. 3.26).

Частный случай - двуполостный гиперболоид вращения.

Следует отметить, что все поверхности второго порядка, за исключением параболического и гиперболического цилиндров, а также гиперболического параболоида, могут пересекаться плоскостью по окружности, т.е. имеют круговые сечения.

3.8 Циклические поверхности

Циклическими поверхностями называются поверхности, которые образованы движением окружности переменного радиуса по определенному закону. Следовательно, всякой цилиндрической поверхности принадлежит семейство окружностей. Второе семейство линий (направляющих) может состоять из различных кривых в зависимости от закона движения образующих, который задается аналитически или графически.

Одним из видов циклических поверхностей являются каналовые поверхности, которые образуются движением окружности переменного радиуса так, что центр окружности перемещается по заданной кривой (линии центров) l, а плоскость окружности остается перпендикулярной к этой кривой (рис. 3.27).

На комплексном чертеже каналовую поверхность можно задать посредством линии центров и одной из образующих. Линия центров определяет закон движения окружности, а образующая – закон изменения радиуса.

Ф (l, b) – каналовая поверхность. к – одна из образующих Ф.

Горизонтальные проекции образующих можно построить по двум осям. Горизонтальная проекция отрезка строится как огибающая проекция образующих.

3.9 Пример составления уравнения циклической поверхности

В качестве примера рассмотрим циклическую поверхность которая: образуется движением окружности постоянного радиуса. Плоскости окружностей поверхности параллельны между собой, центр окружности М перемещается по прямой f (рис. 3.28). Уравнение линии центров: y₀ = 0, z₀ = x₀.

Уравнение окружности:

(x-x₀)² + (y-y₀)² = z², z = z₀

Где x_0, y_0, z₀ – координаты центра окружности.

Очевидно, что координата точки окружности равна координате z₀ ее центра, следовательно, x₀ = z₀ = z.

Подставляя значения координат центра окружности в уравнение окружности, получим уравнение поверхности:

(x-z)² + y² = r².

Эта поверхность называется эллиптическим цилиндром.

3.10 Графические поверхности

В инженерной практике нередко возникает необходимость графического отображения процессов или объектов, которые описываются сложными уравнениями, либо для них не существует точной математической модели из-за сложности процесса или недостаточной его изученности. В таких случаях рассматриваемые процессы о объекты моделируются посредством поверхностей, которые на чертеже изображаются при помощи совокупности линий (дискретного каркаса). Такие поверхности называются графическими.

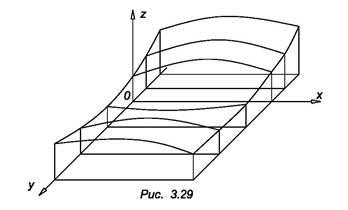
К графическим поверхностям относятся поверхности земной коры, корпуса судна, обшивки самолета, автомобиля, рабочая поверхность лопатки газотурбинного двигателя, поверхность термодинамического потенциала и др. (рис. 3.29). Геометрические модели графических поверхностей несут необходимую информацию и позволяют проводить приближенные расчеты.

4. Взаимное положение поверхностей

Известны три случая взаимного положения поверхностей:

· Поверхности не пересекаются или не имеют общих действительных точек;

· Поверхности касаются, т.е. имеют общие двойные точки или линии;

· Поверхности пересекаются, т.е. имеют одну или несколько общих линий.

Если рассматриваемые поверхности не пересекаются, интерес представляет только задача по определению видимости их контуров, которая может быть решена уже рассмотренными методами.

Случай касания поверхностей рассмотрим на примере касания сферы и плоскости.

Задача: через точку М, принадлежащую сфере, провести плоскость, касательную к сфере (рис. 4.1).

1. Через точку М проведем горизонталь поверхности – окружность k.

2. h – касательная к окружности k в точке М.

3. Через точку М проведем фронталь поверхности n, где n – окружность.

4. f – касательная к окружности n. Пересекающиеся прямые h и f определяют искомую плоскость.

Если поверхности пересекаются, то линию пересечения поверхностей обычно строят по ее отдельным точкам, которые определяются способом вспомогательных секущих поверхностей. Суть его заключается в следующем:

1. Две данные поверхности пересекают некоторой вспомогательной поверхностью.

2. Строят линии пересечения вспомогательной поверхности с данными поверхностями.

3. Определяют общее точки этих линий.

4. Повторяя указанный прием с различными вспомогательными поверхностями, находят такое количество точек, которое графически вполне определяет линию пересечения.

5. После этого полученные точки соединяют с учетом видимости плавной кривой линией с помощью лекала.

Решая задачи на определение линии пересечения поверхностей, следует помнить, что кроме произвольных общих точек линия пересечения имеет особые или спорные точки. Это точки, принадлежащие очерковым линиям, экстремальные точки, точки перегиба и др. Эти точки следует определять по возможности точнее.

В качестве вспомогательных поверхностей следует выбирать такие поверхности, которые пересекают данные по наиболее простым линиям. Чаще всего это плоскости или сферы.

4.1 Метод вспомогательных секущих плоскостей

Для построения линии пересечения поверхностей во многих задачах удобно использовать совокупность вспомогательных плоскостей уровня.

Задача: построить линию пересечения кругового конуса Q и эллиптического цилиндра Ф (рис. 4.2).

Алгоритм решения задачи:

1. Г – вспомогательная плоскость, Г ║ П₁ (рис. 4.2).

2. Г П Q = p; Г П Ф =g.

3. p П g = М, М^’.

4. Выбираем другие вспомогательные плоскости и повторяем действия с 1 по 3 для каждой из плоскостей, до тех пор пока не будет построено необходимое количество точек (рис. 4.3).

Замечание: в числе вспомогательных плоскостей следует обязательно выбирать плоскости симметрии заданных поверхностей и плоскости крайних параллелей и меридианов. На рис. 4.3 это плоскости Г^” и ∑.

5. Соединяем полученные точки плавной кривой линией с учетом видимости.

Участок линии является видимым только в том случае, если все его точки принадлежат видимой части данных поверхностей.

Для решения задач на взаимное пересечение поверхностей иногда полезно применять методы преобразования комплексного чертежа.

Задача. Построить линию пересечения конуса Q с плоскостью общего положения О.

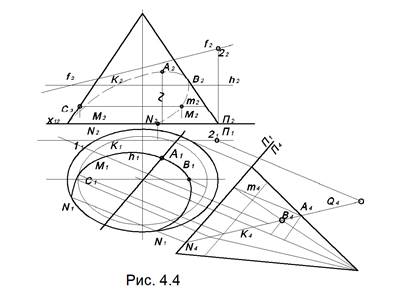
На рис. 4.4 плоскость О задана горизонталью h и фронталью f. Решение задачи намного упроститься, если с помощью метода замены плоскостей проекций выбрать дополнительную плоскость проекций П₄ так, чтобы данная плоскость проецировалась на нее в прямую. Это станет возможным в том случае, если П_{4 ┴} О.

Алгоритм решения:

1. Выбираем П₄, П_{4 ┴} П₁, П_{4 ┴} О, следовательно, x_{14 ┴} . Строим проекции конуса и плоскости О на П₄. Линия пересечения на П₄ спроецируется в отрезок прямой k₄, k₄ = О₄. Чтобы найти О₄ достаточно построить дополнительные проекции двух точек 1 и 2.

2. Выделим на k₄ особые и промежуточные точки, необходимые для построения проекций k₁ и k₂ линии пересечения. К ним относятся точки: А – наивысшая, В и С принадлежат фронтальному очерку, N и N^’ – наинизшие. М и М^’ – промежуточные точки.

3. Построим горизонтальные, а затем фронтальные проекции этих точек по принадлежности конической поверхности или плоскости.

4. Соединим полученные точки плавной кривой линией к с учетом видимости, считая плоскость прозрачной.

При построении линии пересечения конических и цилиндрических поверхностей общего вида целесообразно выбирать вспомогательные секущие плоскости общего положения.

В случае пересечения конических поверхностей эти плоскости должны проходить через вершины конусов, тогда они пересекают обе поверхности по прямолинейным образующим. Если пересекаются цилиндрическая и коническая поверхности, то вспомогательные поверхности должны проходить через прямую, проведенную через вершину конуса параллель образующей цилиндра. В случае же пересечения двух цилиндрических поверхностей вспомогательные плоскости должны быть параллельны некоторой плоскости, определяемой двумя пересекающимися прямыми, соответственно параллельным образующим цилиндрических поверхностей.

4.2 Метод вспомогательных секущих сфер

Если пересекающиеся поверхности являются поверхностями вращения или содержат семейства окружностей, то в качестве вспомогательных поверхностей целесообразно использовать сферы.

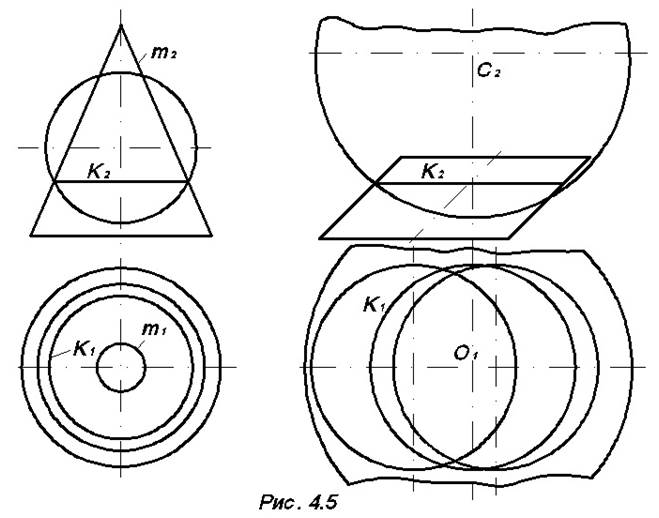
На рис. 4.5 показаны примеры пересечения сферы с конусом вращения и сферы с эллиптическим цилиндром (сферу здесь считаем прозрачной). В первом случае центр сферы принадлежит оси вращения конуса, а во втором – расположен на перпендикуляре, восстановленном из центра окружности поверхности цилиндра к плоскости окружности. Линией пересечения поверхностей в том и другом случае являются окружности.

Рассмотрим на примерах два случая применения вспомогательных сфер.

Методом концентрических сфер можно пользоваться, если выполнены следующие условия:

· Пересекаются две поверхности вращения

· Оси вращения поверхностей пересекаются

· Общая плоскость симметрии поверхностей параллельна плоскости проекций. Это условие не является обязательным.

Задача. Построить линию пересечения конуса вращения Q (а, i) с тором Т (l, j) (рис 4.6).

Пересекающиеся поверхности имеют общую плоскость симметрии Ф, Ф║ П₂, I П j = о. Плоскость Ф пересекает данные поверхности по контурным образующим, которые пересекаются в точках А и В. Эти точки ограничивают фронтальную проекцию линии пересечения, следовательно, радиус наибольшей вспомогательной сферы равен большему из отрезков /О₂В₂/ или /О₂А₂/.

Нетрудно догадаться, что наименьшая сфера должна быть вписана в одну из поверхностей и пересекать вторую поверхность. В данном случае эта сфера вписана в тор. Она касается тора по окружности h и пересекает конус по окружности k. Эти окружности пересекаются, т.к. принадлежат одной сфере, и точки их пересечения С = С^’ принадлежат искомой линии. (Горизонтальная проекция этих точек определяется по принадлежности вспомогательной окружности h).

Чтобы построить промежуточные точки будем выбирать сферы с радиусом больше радиуса минимальной сферы, но меньше радиуса максимальной. Построение промежуточных точек показано на рис. 4.7.

1. R – вспомогательная сфера.

2. R П T = m; R П Q =n.

3. m П n = М.

4. Изменяя радиус вспомогательных сфер, получим необходимое количество точек искомой линии.

5. Полученные точки следует соединить плавной кривой линией с учетом видимости.

Заметим, что точка видимости D на горизонтальной проекции линии пересечения принадлежит горизонтальному очерку цилиндра, поэтому следует предварительно уточнить положение этой точки на фронтальной проекции и затем на горизонтальной.

Метод вспомогательных эксцентрических сфер применяется в тех случаях, когда одна из пересекающихся поверхностей является поверхностью вращения, а вторая содержит семейство окружностей.

Задача. Построить линию пересечения тора Т и сферы Q/

По аналогии с предыдущей задачей строим точки А и В в общей плоскости симметрии Ф. (рис. 4.8).

Точка А в данном случае является наивысшей точкой искомой линии, а точка В – наименьшей. Следовательно, окружность на торе следует выбирать в этих пределах.

Пусть m одна из таких окружностей, m = ∑ П Т. Центры всех сфер, проходящих через эту окружность, принадлежат перпендикуляру n, восстановленному к плоскости окружности из ее центра. Но вспомогательная сфера должна пересекать по окружности и другую поверхность, т.е. центр ее должен быть расположен и на оси вращения i поверхности Q. Следовательно, центром вспомогательной сферы является точка О = I П n, радиусом отрезка О₂К₂, где К₂ – контурная точка окружности m.

Вспомогательная сфера пересекает сферу Q по окружности b. Окружности m и b пересекаются в точках М и М^’, принадлежащих искомой кривой. Меняя положение плоскости ∑ в указанных пределах и повторяя рассмотренные действия, построим необходимое количество точек искомой линии и соединим их плавной кривой линией с учетом видимости (см. рис. 4.8).

4.3 Особые случаи пересечения поверхностей второго порядка

В общем случае две поверхности второго порядка (квадрики) пересекаются по кривой четвертого порядка, но в некоторых случаях кривая четвертого порядка распадается на:

· Кривую третьего порядка и прямую, если пересекаются линейчатые квадрики (например, цилиндр и конус) с общей образующей;

· Четыре прямые, например, при пересечении двух цилиндров второго порядка с параллельными образующими;

· На две кривые второго порядка (коники).

Случаи, когда линия пересечения квадрик распадается на две коники, а также когда линия пересечения, являясь кривой четвертого порядка, проецируется в кривую второго порядка, перечислены в следующих четырех теоремах.

Теорема 1. Если две квадрики имеют общую плоскость симметрии, параллельную плоскости проекций, то линии их пересечения на эту плоскость проецируются в кривую второго порядка.

На рис. 4.3 пересекаются квадрики с общей плоскостью симметрии ∑, ∑ ║ П₂, следовательно, линия пересечения этих квадрик симметрична относительно ∑, и каждая пара симметричных точек на П₂ спроецируется в одну точку, т.е. порядок проекции линии пересечения уменьшится в два раза, и кривая пересечения четвертого порядка спроецируется на П₂ в кривую второго порядка.

Теорема 2. Если две квадрики имеют общую конику, то линия их пересечения распадается на две коники. Доказательство этой теоремы тривиально: 4-2-2. Пример применения теорем 1 и 2 показан на рис. 4.9.

Эллиптические конус и цилиндр имеют общую окружность m – это одна часть линии пересечения данных поверхностей. Другая часть линии пересечения – коника k, на плоскость П₂ она проецируется в отрезок прямой k₂, т.к. поверхности имеют общую плоскость симметрии Ф. Следовательно, для построения k₂ достаточно найти две точки, проще всего построить точки А и В с помощью вспомогательной плоскости ф. Если точка В₂ недоступна, то можно построить любую точку искомой линии, например М, воспользовавшись вспомогательной плоскостью Г.