Высшего профессионального образования 2 страница

Если не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Плоскости общего положения бывают восходящими и нисходящими.

Если плоскость по мере удаления от наблюдателя поднимается вверх, то она называется восходящей. Чтобы избежать недоразумений, удаление надо производить по профильной прямой, принадлежащей плоскости. На комплексном чертеже восходящей плоскости обе проекции треугольника, ей принадлежащего, ориентировано одинаково (рис. 2.16), а для нисходящей – противоположно (рис. 2.13).

Если плоскость параллельна или перпендикулярна одной плоскостей проекций, то она называется плоскостью частного положения. Различают следующие виды плоскостей частного положения:

1. 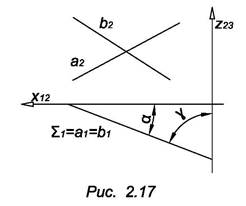Плоскость, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально проецирующей плоскостью. Все точки и прямые такой плоскости на горизонтальную плоскость проекций проецируются в прямую, например, Z₁ (рис. 2.17) – проекция плоскости 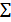, 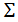_┴ П₁; а,b € 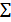. Фронтальная и профильная проекции ее занимают соответственно все поле проекций П₁ и все поле проекций П₃. Очевидно, что а и ᵞ - углы наклона плоскости 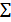, к фронтальной и профильной плоскостям соответственно.

2. Плоскость, перпендикулярная к фронтальной плоскости проекций, называется фронтально проецирующей плоскостью, ее фронтальная проекция является прямой, а горизонтальная и профильная проекции занимают соответственно все поле проекций П₁ и все поле проекций П₃ (рис. 2.18). Фронтально проецирующая плоскость Т вполне определяется ее одной проекцией Т₂. Углы β и u измеряют углы наклона плоскости к плоскостям проекций П₁ и П₃ соответственно, А € Т.

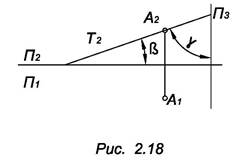
3. Плоскость, перпендикулярная к профильной плоскости проекций, называется профильно проецирующей плоскостью, ее профильная проекция является прямой, а горизонтальная и фронтальная проекции занимают соответственно все поле проекций П₁ и все поле проекций П₂ (рис. 2.19). Профильно проецирующая плоскость О вполне определяется ее одной проекцией О₃. Углы а и β измеряют углы наклона плоскости О к плоскостям проекций П₁ и П₂ соответственно. n € О, m € О.

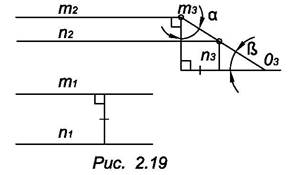
4. Плоскость, параллельную какой – нибудь плоскости проекций, называют плоскостью уровня, так как все точки этой плоскостью одинаково удалены от соответствующей плоскости проекций (рис. 2.20).

Плоскость Г, параллельную горизонтальной плоскости проекций, называют горизонтальной плоскостью уровня, а, b € Г.

Плоскость Ф, параллельную фронтальной плоскости проекций, называют фронтальной плоскостью уровня, А, l €Ф.

Плоскость Р, параллельную профильной плоскости проекций называют профильной плоскостью уровня.

Очевидно, что каждая плоскость уровня является в то же время проецирующей плоскостью. Фигуры, принадлежащие горизонтальной плоскости Г, фронтальной плоскости Ф или профильной плоскости Р проецируется без искажения соответственно на плоскость проекций П₁, П₂ или П₃.

2.5 Взаимное положение точки, прямой и плоскости

Задачи на взаимное положение геометрических элементов называются позиционными.

Точка принадлежит плоскости, если она принадлежит какой – либо прямой этой плоскости. Например, точка К € G (А, В, С), т.к. К € В1 и G1 € О (А, В, С) (рис. 2.21). Очевидно, что N не принадлежит плоскости О, т.к. точка N не принадлежит ни одной из двух прямых АВ или АС. Про точку N можно сказать, что она расположена над плоскостью О, т.к. она расположена над прямой АС. Известно, что точка M € О, а точка L расположена над точкой М, следовательно, точка L находится над плоскостью О.

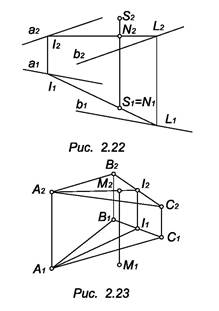
Задача. Дана восходящая плоскость Э (а ║b), построить точку S над плоскостью, если известна ее горизонтальная проекция S₁ (рис. 2.22).

Точка S₂ должна располагаться над вспомогательной прямой 12, принадлежащей плоскости О и следовательно, над точкой N € 12. Очевидно, что задача имеет бесконечное множество решений.

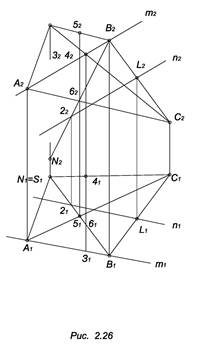
Обратная задача. Определить положение точки М относительно плоскости R (А, В, С). М ближе R, т.к. М ближе А1 € R (рис. 2.23).

Задача. Построить проекции треугольной пирамиды, основание которой принадлежит данной плоскости Q, а вершина расположена над плоскостью. Определить видимость ребер пирамиды.

Эта задача состоит из трех элементарных задач.

1. Построить вершины А, В, С в плоскости Q. Точки А и В выберем на прямой m, а точку С на вспомогательной прямой В1 (рис. 2.24).

2. Построить точку S над плоскостью Q. Выберем некоторую точку N, принадлежащую Q. На рис. 2.25 эта точка принадлежит В2 € Q. Точка S д.б. над точкой N.

Q (m ║ n) – нисходящая плоскость.

3. На рис. 2.26 повторены эти действия и через полученные точки проведены ребра искомой пирамиды.

Контурные ребра на всех плоскостях проекций всегда видимые.

Для определения видимости ребер АС и SB на горизонтальной плоскости проекций следует воспользоваться горизонтально конкурирующими точками 5 и 6 на этих ребрах. По фронтальной проекции видно, что точка 5 выше точки 6, следовательно, на горизонтальной проекции видимыми являются точка 5 и ребро АС, которому она принадлежит. Аналогично определяется на фронтальной проекции видимость ребер АВ и SC посредством фронтально конкурирующих точек 3 и 4.

2.6 Кривые линии и их проекции

Понятие о линиях как и о других геометрических объектах приобретается из опыта. Кривую линию можно рассматривать как границу части поверхности, или как результат пересечения двух поверхностей, или как множество последовательных положений непреровно перемещающейся в пространстве точки.

Положение точки на линии может быть определено одним параметром, следовательно, линия является однопараметрическим множеством точек..

Назовем два способа классификации кривых линий:

1. Кривые бывают плоские, пространственные и многомерные.

2. Кривые могут быть закономерными и незакономерными.

Закономерные кривые могут быть заданы и аналитически и графически. Незакономерные задаются только графически.

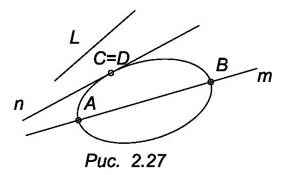В зависимости от вида уравнения кривой закономерные кривые бывают алгебраические и транссидентные. Степень алгебраического уравнения определяет порядок кривой. Геометрически порядок плоской кривой определяется по числу точек пересечения ее с прямой, принадлежащей плоской кривой. Точки пересечения могут быть действительными и мнимыми. Например, эллипс пересекается с прямой m в двух действительных точках А и В, с прямой n в двух совпавших действительных точках, с прямой l в двух мнимых точках (рис. 2.27). Если составить уравнение эллипса и прямой m, то, решая их совместно, получим уравнение второго порядка, дискриминант которого положительное число. Во втором случае дискриминант равен нулю, а в третьем - дискриминант отрицателен.

Проекции плоскости кривых линий обладает следующими основными свойствами:

1. В общем случае порядок плоской алгебраической кривой при параллельном проецировании не изменяется.

2. Бесконечно удаленные точки кривой проецируются в бесконечно удаленные точки ее проекций.

3. Касательная к кривой проецируется в касательную к ее проекции

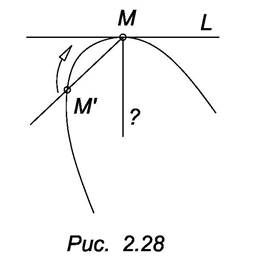Касательной t в точке М плоской кривой l будем называть предельное положение секущей ММ^’, когда М, оставаясь на линии l, стремиться к точке М (рис. 2.28). Нормалью n к кривой l в точке М называют прямую, принадлежащую плоской кривой и перпендикулярную к касательной в этой точке.

2.7 Линии второго порядка

В общем случае кривая второго порядка задается уравнением второго порядка вида:

Аx² +By² + C_xy + D_x + E_y + 1 = 0

(Если свободный член уравнения не равен 1, то обе части уравнения можно разделить на свободный член).

Следовательно, кривую второго порядка определяют пять параметров А, В, С, D, Е. Эти параметры можно вычислить, взяв координаты пяти точек данной кривой. Пусть известны точки: М₁ (x₁y₁), М₂ (x₂y₂), М₃ (x₃y₃), М₄ (x₄y₄) и М₅ (x₅y₅). Для определения коэффициентов А, В, С, D, Е следует решить систему из пяти линейных уравнений:

Аx₁² + Вy₁² + Cx₁y₁ + Dx₁ + Ey₁ + 1 = 0

Аx₂² + Вy₂² + Cx₂y₂ + Dx₂ + Ey₂ + 1 = 0

Аx₃² + Вy₃² + Cx₃y₃ + Dx₃ + Ey₃ + 1 = 0

Аx₄² + Вy₄² + Cx₄y₄ + Dx₄ + Ey₄ + 1 = 0

Аx₅² + Вy₅² + Cx₅y₅ + Dx₅ + Ey₅ + 1 = 0

Следовательно, кривую второго порядка в общем случае можно задавать пятью точками или набором из пяти других геометрических элементов, например, двумя касательными и тремя точками. Подробнее с этим вопросом можно познакомиться по учебнику.

Если кривая второго порядка задана уравнением в общем виде, то пользуясь поворотом и переносом осей координат, ее уравнение можно привести к пяти частным случаям, которые перечислены в таблице 2.1.

Таблица 2.1 Уравнения. Определения и основные понятия кривых второго порядка

Кривая	Основные понятия	Чертеж
Окружность x2 + y2 =R Множество точек равноудаленных от данной точки на данное расстояние Уравнение (x-a)2 + (y-b)2 = R2, где a, b – координаты центра, R – радиус. Если центр в начале координат, то x2 + y2 = R2	/ОМ/ - радиус окружности 12 – диаметр окружности О – центр окружности (12) и (34) – перпендикулярные диаметры окружности t – касательная окружности (56) и (78) – ортогонально – сопряженные диаметры окружности (q10) – хорда ортогонально – сопряженная диаметру (78)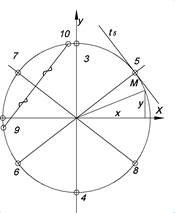
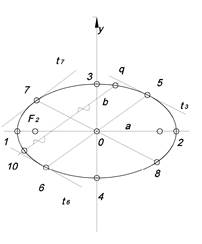
Эллипс 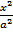  + 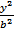= 1 Множество точек, сумма расстояний которых до двух данных точек F1 и F2, есть величина постоянная.	(12) – большая ось эллипса (34) – малая ось эллипса С,b – большая и малая полуоси эллипса О – центр эллипса F1, F2 – фокусы эллипса /О F1/ = /О F2/ = 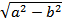(56) и (78) – сопряженные диаметры эллипса t5, t6 – касательные эллипса, сопряженные диаметру (56) t5, t7 – сопряженные касательные (910) – хорд, сопряженная диаметру (78)
Парабола X2 = 2ру Множество точек, для которых расстояние до данной точки F и данной прямой d равны	О – вершина параболы OF – ось параболы t5, - касательная параболы (56) и t5, - сопряженные направления параболы F, d – фокус и директриса параболы. /EF/ = P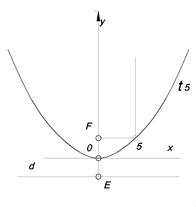
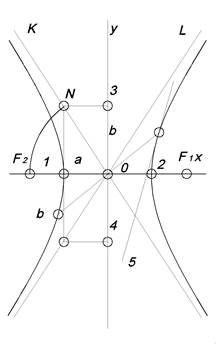
Гипербола 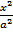- 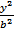= 1 Множество точек, разность расстояний которых до двух данных точек F1 и F2, есть величина постоянная.	1,2 – действительные вершины гиперболы 3,4 – мнимые вершины гиперболы (12) – действительная ось гиперболы (34) – мнимая ось гиперболы (02) – действительная полуось гиперболы (03) – мнимая полуось гиперболы OK и OL – асимптоты гиперболы (56) и t – сопряженные направления гиперболы F1 и F2 – фокусы гиперболы /OF1/ = /OF2/ = /ON/ =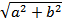

Рассмотрим некоторые способы построения кривых второго порядка.

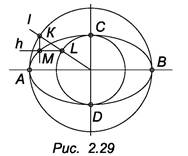
Задача. Построить эллипс по двум осям (рис. 2.29).

Даны:

АВ – большая ось эллипса

CD – малая ось эллипса

О – центр эллипса

1. Проводим две окружности с центром О и радиусом /ОА/ и /ОС/.

2. L – любая прямая проходящая через О.

Прямая l пересекает окружность в точках K и L.

3. Через точку K (K принадлежит большей окружности) проводим прямую f, параллельную малой оси. Через точку L (L принадлежит малой окружности) проводим прямую h, параллельную большой оси эллипса f ║h = М. М принадлежит эллипсу.

4. Меняя положение прямой l, получим множество точек эллипса, которые следует соединить плавной кривой линией.

Задача. Построить параболу (рис. 2.30)

Даны:

А – вершина параболы

AD- направление оси

В – одна из точек.

1. Строим прямоугольник ACBD/

2. Отрезки АС и СВ делим на произвольное и одинаковое число равных частей и нумеруем точки деления как показано на рисунке.

3. Вершину А соединяем с точками деления отрезка СВ, а из точек деления отрезка АС проводим прямые, параллельные оси.

4. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы.

Вторую ветвь параболы можно построить, пользуясь симметрией относительно AD.

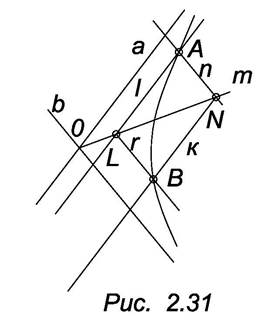
Задача. Построить гиперболу (рис. 2.31).

Даны:

a и b – асимптоты,

а П b = О,

А – некоторая точка гиперболы.

1. Через точку А проведем прямые n и l, параллельные асимптотам b и a соответственно.

2. Через центр гиперболы О проведем произвольную прямую m. m П n = N; m П l =L.

3. Через точку N проведем прямую k, k ║ а; и через точку L прямую r, r ║ b.

4. k П r = B, B – принадлежит искомой гиперболе.

Меняя положение прямой l, получим ряд точек гиперболы.

2.8 Пространственные кривые

Пространственные кривые задаются системой из двух уравнений y = f(x), z = u(x) или T (x, y, z) = 0, u (x, y, z) = 0, т.е. фактически уравнениями заданы две поверхности, пересечением которых определена кривая.

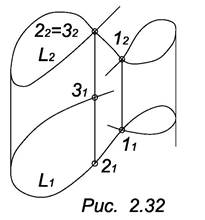
Для задания пространственной кривой на чертеже необходимы две проекции. На рис. 2.32 изображена пространственная кривая. Очевидно, что эта кривая имеет оду особую (двойную) точку 1. Точки 2 и 3 – различные точки.

3. Поверхности

3.1 Образование, задание и изображение поверхностей

Поверхность в начертательной геометрии рассматривается как непрерывная совокупность последовательных положений переменной образующей, перемещающейся в пространстве по определенному закону. Таким способом образования поверхности называется кинематическим. Линия при своем движении может оставаться неизменной или непрерывно меняться.

Поверхности могут быть заданы аналитически, то есть уравнением (алгебраические поверхности и трансцендентные) и графически - на чертеже.

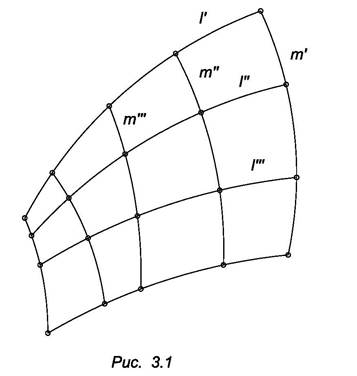
На любой поверхности можно выделить два семейства кривых линий: семейство l и семейство m, каждое из которых покрывает всю поверхность и состоит из каких – либо линий (рис. 3.1). При этом должно соблюдаться условие: никакие две линии одного семейства не должны иметь общих точек и наоборот, каждая линия одного семейства должна пересекать все линии другого семейства.

В этом случае поверхность может быть образована движением линии l, называемой образующей, по неподвижным линиям второго семейства m, которые называются направляющими. Нетрудно видеть, что можно поменять местами образующие и направляющие и при этом получается одна и та же поверхность.

Каждая поверхность может быть образована различными способами. Например, поверхность кругового цилиндра может быть образована вращением прямолинейной образующей вокруг оси, ей параллельной; или движением окружности, центр которой перемещается по оси цилиндра, а плоскость окружности перпендикулярна к оси; или вращением произвольной криволинейной образующей, нанесенной на поверхность цилиндра.

Чтобы задать поверхность на комплексном чертеже, необходимо и достаточно иметь совокупность элементов поверхности и условий, которые позволяют построить каждую ее точку или линию. Такую совокупность называют определителем поверхности. Определитель поверхности содержит геометрическую часть и закон образования поверхности или смысловую часть.

Когда какая – нибудь поверхность проецируется параллельно на плоскость проекций, то проецирующие прямые, касаются поверхности в точках, образующих некоторую линию, называемую контурной линией.

Проекция контурной линии называется очерком поверхности.

Для придания чертежу наглядности в большинстве случаев строят на нем еще и очерк поверхности, а так же ее наиболее важные линии и точки.

Принцип образования поверхностей движением линии лежит в основе их изучения в начертательной геометрии. С учетом этого принципа можно сгруппировать поверхности в следующие классы:

1. Поверхности плоско – параллельного перемещения, которые образуются непрерывным параллельным перемещением в пространстве некоторой линии.

2. Поверхности вращения, которые образуются вращением произвольной образующей вокруг неподвижной оси, к их числу относятся поверхности вращения второго порядка.

3. Поверхности второго порядка общего вида

4. Линейчатые поверхности, которые могут быть образованы движением прямой линии, в частности винтовые поверхности, образуемые движением прямолинейной образующей по направляющим винтовым линиям.

5. Циклические поверхности, которые могут быть образованы движением окружности (постоянного или переменного радиуса).

6. Топографические и графически задаваемые поверхности, которые не могут быть образованы по какому – нибудь простому закону и задаются на чертеже семейством некоторых линий (обычно линиями уровня). В этом случае говорят, что поверхность задана дискретным каркасом.

3.2 Поверхности плоско – параллельного перемещения

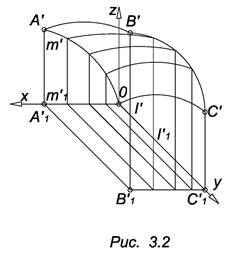
Поверхностью плоско – параллельного перемещения называется поверхность образованная параллельным перемещением кривой линией (образующей) по определенному закону. Закон перемещения может быть задан некоторой кривой, называемой направляющей.

Если направляющая m задана уравнением z = f(x), y = 0, а образующая: z = u(y). X = 0 (рис. 3.2), то уравнение поверхности имеет вид:

Z = f(x) + u(y).

Если образующая поверхности – прямая, то поверхность относится также к классу линейчатых поверхностей (цилиндрическая поверхность).

3.3 Поверхности вращения

Поверхностью вращения называется поверхность, образованная вращением линии (образующей) вокруг некоторой неподвижной прямой (оси вращения). Определитель: Ф (I, l) – поверхность вращения. Геометрическая часть определителя Ф (I, l) должна состоять из оси вращения i и образующей l (рис. 3.3). Смысловая часть содержит информацию о названии поверхности и, следовательно, задает закон образования поверхности.

Каждая точка образующей l при вращении вокруг оси i описывает окружность p (параллель поверхности), расположенную в плоскости, перпендикулярно оси вращения. Центр О окружности p находится в точке пересечения оси вращения с плоскостью окружности, а радиус равен расстоянию от взятой точки образующей до оси вращения.

Наибольшая е и наименьшая g параллели называются соответственно экватором и горловиной (рис. 3.4).

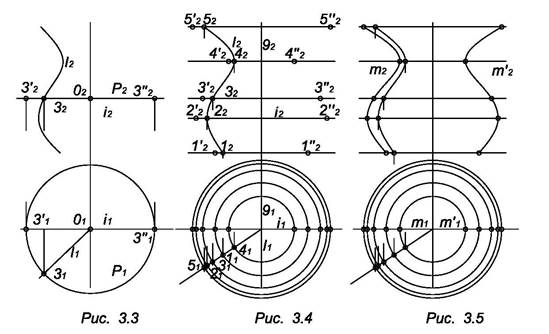
Кривые линии поверхности вращения, плоскость которых проходит через ось вращения, называется меридианами, например, l, m, m^’.

Все меридианы одной поверхности вращения конгруэнтны (рис. 3.5).

На комплексном чертеже целесообразно ось вращения выбирать перпендикулярно одной из плоскостей проекций.

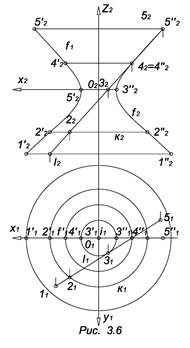В качестве примера рассмотрим комплексный чертеж гиперболоида вращения. Однополостный гиперболоид вращения образуется вращением прямой l вокруг скрещивающейся с ней оси i. Заданием этих элементов на комплексном чертеже поверхность определена, но для решения ряда задач и для наглядного изображения поверхности необходимо строить каркас и очерк поверхности, заданной определителем. На прямой l выберем несколько точек (1,2,3,4,5) и построим проекции параллелей, описываемых этими точками (рис. 3.6).

Например, параллель k проходит через точку 2. Горизонтальная проекция ее – окружность, радиус которой i2. Фронтальная проекция – отрезок прямой конгруэнтный диаметру окружности k. Точки 2 и 2^’ принадлежат фронтальному очерку поверхности f. Меридиан f называется главным меридианом поверхности. Заметим, что главным меридианом рассматриваемой поверхности является гипербола, и, следовательно, гиперболоид вращения может быть образован вращением гиперболы вокруг оси.

На поверхности однополостного гиперболоида имеются два семейства прямолинейных образующих. Образующие каждого семейства между собой скрещиваются, но всякая образующая одного семейства пересекает все образующие другого. Поэтому через каждую точку поверхности можно провести две прямолинейные образующие равных семейств. Т.о., каркас однополостного гиперболоида вращения может быть составлен из множества окружностей или на множестве прямых. Если линии каркаса принять за оси металлических стержней и колец, то получится реальная инженерная конструкция – экономичная, прочная и жесткая. Эта конструкция может служить опорой, мачтой, каркасом гиперболических оболочек.

3.4 Уравнение поверхности вращения

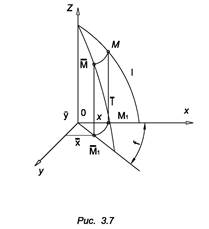Пусть известно уравнение главного меридиана поверхности вращения (рис. 3.7):

Z = f(x), y = 0. (3.1)

Тогда точка этого меридиана М (x, O, y) после поворота на некоторый угол t займет положение 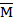(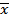, , 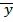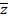) на меридиане 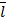. По чертежу видно, что

Z =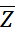

X =

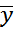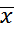= tg t.

Подставляя эти значения в уравнения (3.1), получим систему уравнений, которые задают любой меридиан поверхности вращения:

z = f()

y = x tg t

Здесь 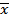, , 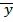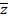- текущие координаты, следовательно, целесообразно эти уравнения записать в виде:

z = f (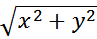) (3.2)

y = x tg t (3.3)

Уравнение (3.2) – уравнение поверхности, а уравнение (3.3) – задает плоскость меридиана.

Итак, для того чтобы получить уравнение поверхности вращения, необходимо в уравнение ее главного меридиана вместо переменной x подставить 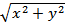(имеется ввиду, что ось вращения поверхности совпадает с осью Oz).

Используя этот прием, выведем уравнения рассмотренных ранее поверхностей вращения и проведем их краткое исследование.

1. Поверхности, образованные вращением прямой вокруг некоторой оси. К ним относятся поверхности однополостного гиперболоида вращения, конуса и цилиндра вращения.

Математическая модель:

- гиперболоида (см. рис. 3.6) имеет вид:

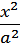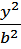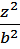+ - = 1,

Уравнение главного меридиана: 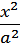- 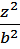= 1,

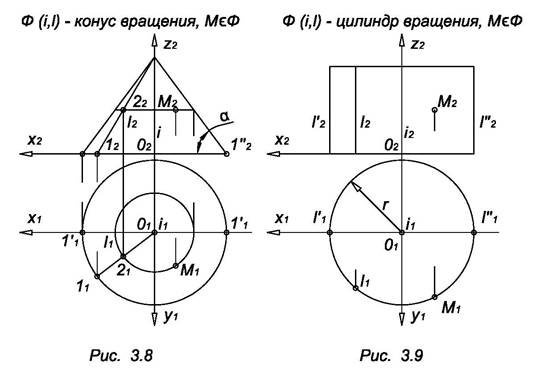
- конуса вращения (см. рис. 3.8) имеет вид:

(z – a)² = k² (x² + y²),

k = tga;

- цилиндра вращения (рис. 3.9) имеет вид:

x² + y² = r²

2. Поверхности вращения, образованные вращением окружности или ее дуги. К ним относятся сфера и тор.

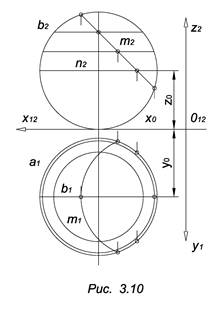
Сфера образуется, если окружность вращается вокруг оси, проходящей через ее центр (рис 3.10). Уравнение сферы имеет вид:

(x – x₀)² + (y – y₀)² + (z – z₀)² = r²,

Где x₀, y_0, z₀ – координаты центра сферы.

На рис. 3.10

а – экватор,

b – главный меридиан,

m – линия, принадлежащая поверхности.

Линия m является плоской кривой, принадлежащей сфере, следовательно, m – окружность. Ее горизонтальная проекция эллипс m₁, большая ось которого А₁В₁, а малая С₁D₁. Это обусловлено тем, что диаметр АВ окружности m параллелен плоскости П₁ и проецируется на П₁ в натуральную величину. Концы диаметра А₁ и В₁ строятся по принадлежности параллели k (k₂ проходит через середину отрезка m₂).