Примеры реализации и решения задачи определения минимума функции цели в среде mathcad

Пусть задана многоэкстремальная функция:

.

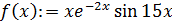Рассмотрим ее графики при различных изменениях . Из первого графика видим, что глобальный экстремум находится в районах 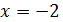и равен примерно 75.

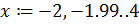
Если смотреть другую область изменения, то глобальный экстремум находится в районе . Рассмотрим область изменения .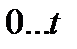

Используем метод «Монте-Карло» для нахождения глобального минимума функции. Сформируем два вектора 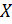и 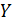, присвоив их нулевым элементам значение нуль:

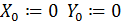
Зададим количеством случайных чисел 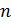, которое мы будем использовать для вычисления минимума. Чем больше это количество, тем точнее будет результат вычисления:

.

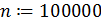С помощью функции создадим вектор случайных значений элементов 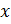. Функция 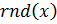генерирует равномерно распределенные случайные числа в интервале 0… .

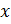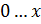
Из графика видно, что нам достаточен интервал .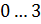

.

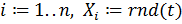Теперь в векторе 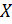помещено 100000 случайных чисел. Вычислим значения функции от них и поместим их в вектор .

.

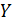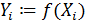Величину минимального элемента этого вектора найдем, используя функцию .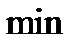

Величину минимального элемента вектора 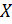найдем, используя небольшую программу и вычислим по ней ответ:

,

,

.

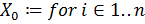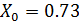Получили первое приближенное значение минимума функции цели. Для уточнения значения используем градиентный метод. Поиск минимума ведется по следующим формулам:

,

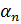выбирается из условия .

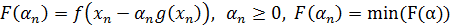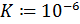– параметр, определяющий погрешность поиска минимума.

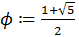- отношение золотого сечения.

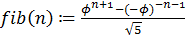- формула Бине

для вычисления чисел Фибоначчи, где 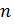– номер числа.

Сделаем подпрограмму для вычисления частной производной функции 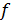в точке заданной вектором 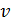по переменной .

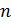Подпрограмма выглядит следующим образом:

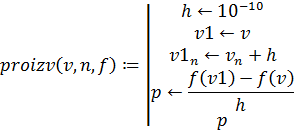
Сделаем подпрограмму для вычисления значений проекций градиента на оси координат. Подпрограмма возвращает вектор значений проекций и использует подпрограмму вычисления частной производной:

.

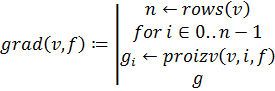Функция , используемая для выбора :

.

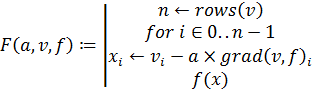Далее сделаем подпрограмму поиска минимума функции одной переменной по методу Фибоначчи (одномерной оптимизации функции цели).

Подпрограмма поиска минимума с помощью метода градиентного спуска:

Сформулируем еще раз нашу многоэкстремальную функцию:
,

.

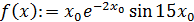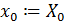Находим, в какой точке 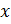достигается минимум функции цели по нашей программе:

.

Находим значение минимума функции цели:

.

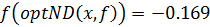Отсюда можно сказать, что метод градиентного спуска подтвердил сходимость решения методом «Монте-Карло», [9, 10].

Пример из расчетного эксперимента:

Заключение

Целью нашего рассуждения и последующего исследования в работе является сведение полученной задачи НМП (18) к классической задаче математического программирования (2), для той же целевой функции , [3, 5, 8-11].

Приложение: рисунки и таблица

Рис. 1. Принципиальная модульно-структурная схема ВК для SKAIS ТЭС

с теплофикационными установками.

Рис. 2. SKAIS - подсистема диагностики состояния энергоустановки

в контуре управления электростанции.

Рис. 3. Принципиальная блок – схема 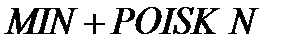модуля .

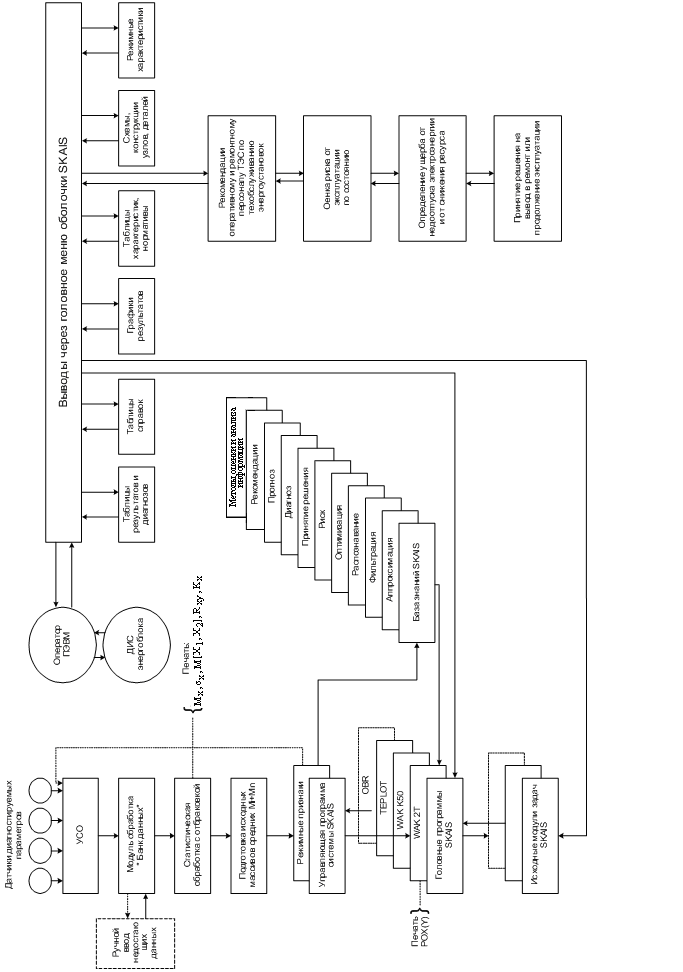
Рис. 4. Диагностический комплекс SKAIS (реализованный вариант).

Рис. 5. «Похожесть» диагностируемого состояния (при сравнении с нормативным значением 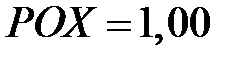) и определение фактического значения (общее состояние энергоустановки) как расстояния между ними, определяемое по формуле 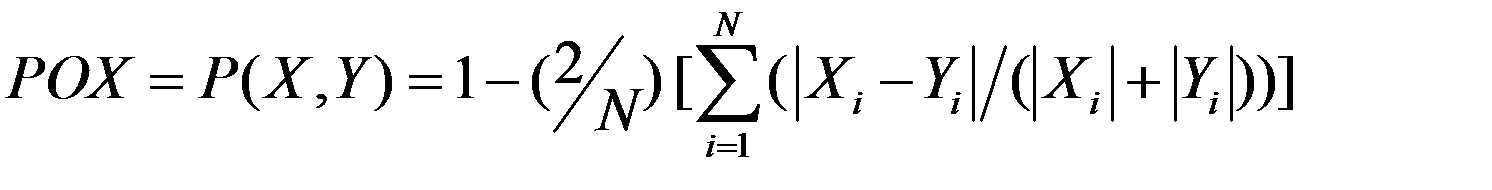[9]:

,[9].

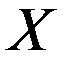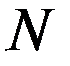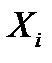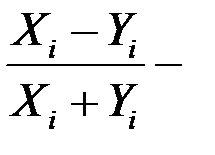Здесь - вектор измеренных параметров; - вектор эталонных значений параметров; - количество анализируемых параметров; - наборы значений признаков (параметров состояния) для диагностируемого () и эталонного () объектов (агрегатов), коэффициент Фехнера (см. закон Вебера-Фехнера, , где 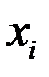- оценка некоторой величины при «ощущении» ).

При этом, 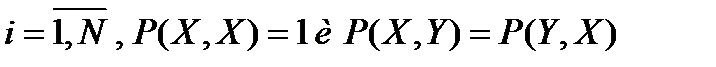. Если известно 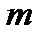элементов – эталонов , где 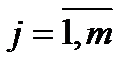, то, используя понятие «похожесть», можно найти ближайший к данному объекту 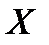(его состоянию) эталон по максимуму значения коэффициента 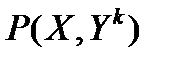, где .

Таблица П.1

Массив «весов» параметров-признаков (отклонение мощности турбины ΔN_Э и ее экономичности Δ 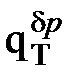от гарантийного значения, DELTA = ΔN_Э/Δ 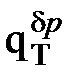) турбоустановки

Т – 100 – 130 ТМЗ ст. №7 Н ТЭЦ – 4 (в отдельных опытах до и после ремонта) и сравнение параметров состояний по мере «похожесть» (РОХ). Режим работы – конденсационный.

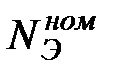
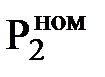
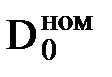
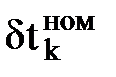
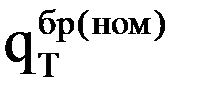
Номинальные (гарантийные) параметры									РОХ	DELTA
МВт	МПа	0С	МПа	т/ч	0С	м3/ч	кДж/ кВт×ч	-	МВт/кДж/кВт×ч
110,0	12,8	555,0	0,0049	480,0	5,8			1,00	-
Фактические параметры	Перед ремонтом	79,73	12,29	552,4	0,0218	392,6	22,5			0,52
75,09	12,29	549,8	0,0216	366,6	14,2			0,65
64,5	12,87	546,0	0,019	326,6	12,6			0,61
55,84	12,94	547,7	0,0156	302,2	13,4			0,57
После ремонта	83,1	12,8		0,0121	330,8	24,7			0,66	0,52/10,05
85,7	12,9		0,0059	339,7	22,2			0,64	0,61/15,9
78,0	12,8		0,0052	323,6	22,2			0,67	0,39/14,2
71,1	13,04		0,0056	289,0	24,3			0,61	0,92/10,9
82,3	12,92		0,0061	332.7	17,1			0,66	0,63/15,9

Здесь под РОХ («похожесть», Рис.5) понимается расстояние между признаками

(точнее их совокупностью образов) состояний энергоустановки близких номинальному (нормативному) состоянию. Похожесть фактического состояния энергоустановки номинальному состоянию определяется по формуле, [9]:

.

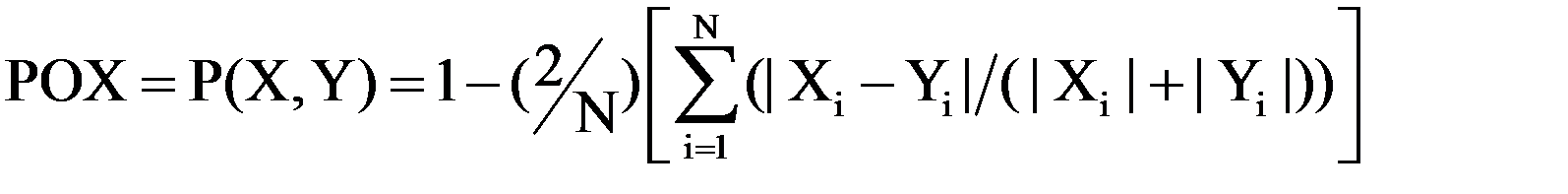Рис.6. Элемент многомерного поиска оптимума (по схеме ) :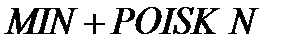

- где взять ближайшую точку – Эвристика! – ближайшая точка совпадает с .