Последовательности

Построенного множества рациональных чисел оказывается недостаточно даже для решения некоторых простейших геометрических задач. Например диагональ единичного квадрата по теореме Пифагора равна числу, удовлетворяющему уравнению x² = 2, которое не имеет решений в поле рациональных чисел. Действительно, предположим противное: пусть рациональное число 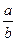является решением уравнения x² = 2, то есть (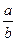)² = 2. Не нарушая общности, будем считать, что 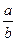– несократимая дробь (в противном случае её можно было бы сократить). Так как (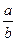)² = 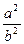= 2, то a² = 2b². Правая часть делится на 2, значит и левая делится на 2. 2 – число простое, поэтому если произведение а² делится на 2, то на 2 делится один из множителей, в данном случае это а. Отсюда видно, что a – чётное, то есть a=2k. Тогда

a² = (2k)² = 4k² = 2b².

Следовательно, b² = 2k², а значит и b – чётное число. Таким образом, и а, и b делятся на 2, что противоречит тому, что дробь 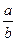несократимая. Противоречие показывает, что исходное предположение неверно, и значит, уравнение x² = 2 не имеет рациональных решений. Положительный корень данного уравнения принято обозначать символом . Это число рациональным не является. Не являются рациональными числами и бесконечные непериодические десятичные дроби (не сложно убедится, что при делении одного целого числа на другое, отличное от 0, всегда получается либо конечная, либо периодическая дробь).

Если целые числа появились в результате невозможности решать уравнения а + х = b в рамках натуральных чисел, рациональные возникли из необходимости решать уравнения ах = b, то можно подумать, что действительные числа появились как результат необходимости решать квадратные уравнения или, быть может, уравнения более высоких степеней. Однако такой подход приводит к построению системы алгебраических чисел, а не действительных. Во-первых, и в рамках действительных чисел не всякое квадратное уравнение имеет решение (например, уравнение х² + 1 = 0), а во-вторых существует весьма широких класс действительных чисел, которые не являются корнями многочленов – это трансцендентные числа. Понятие действительных чисел связано, в первую очередь, с необходимостью вычисления пределов. Хорошо известное трансцендентное число е вводится на основании второго замечательного предела (то есть предела последовательности (1 + 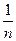)ⁿ_. Другое трансцендентное число p в школьном курсе, как правило, вводится как отношение длины любой окружности к ее диаметру, но и оно может быть определено через понятие предела. Ф. Виетом найдена формула

,

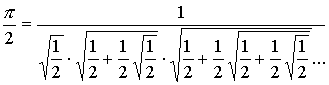где в знаменателе стоит бесконечное произведение, а Г.В. Лейбниц представил 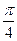в виде бесконечной знакочередующейся суммы

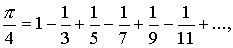
беря все большее число множителей в первой формуле или число слагаемых во второй, можно находить все более точные значения для .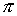

Рассмотрим аксиоматическую теорию действительных чисел, опираясь на понятие предела фундаментальной последовательности.

Определение. Фундаментальная последовательность – это последовательность (a_n), удовлетворяющая условию, что для любого e > 0 существует такой номер n₀, что модуль разности между любыми двумя членами данной последовательности с номерами, большими, чем n₀, будет меньше, чем e.

("e > 0) (∃ n₀ Î N) (" n, m > n₀) |a_n – a_m| < e.

Теорема 1. Всякая сходящаяся последовательность в нормированном поле фундаментальна, но не всякая фундаментальная последовательность сходится.

Доказательство: Предположим, что некоторая последовательность (u_n) имеет предел А. Тогда для любого положительного числа e найдётся такой номер n₀, что для всех членов данной последовательности с номерами большими, чем n₀, |x_n – A| < ε/2.

|u_n – u_m| = |u_n – A + A – u_m| £ | u_n – A | +| A – u_m| < ε/2 + ε/2 < ε,

то есть последовательность (u_n) – фундаментальна. Последовательность же, приближающая число е фундаментальна, но не имеет предела в поле рациональных чисел (Ш. Эрмит доказал, что число е даже не является алгебраическим). То же можно сказать и о последовательности десятичных приближений числа .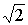

Теорема 2. Если последовательность сходится, то у неё имеется только один предел.

Для доказательства методом от противного предполагают, что имеется два разных предела и в качестве ε выбирают |A – B|/2. В итоге приходят к противоречию |A – B| < |A – B|.

Определение. Последовательность (x_n) называется ограниченной, если существует такое число М > 0, что |x_n| < M.

Теорема 3. Всякая фундаментальная последовательность ограничена.

Доказательство: Так как последовательность фундаментальна, выберем такой номер n₀, чтобы при номерах больших n₀ разность между членами была меньше 1.

|x_n| = |x_n – x_n0 +x_n0| £ |x_n – x_n0| + |x_n0| < 1 + |x_n0|.

Далее находим М – наибольшее, среди модулей членов, предшествующих |x_n0|, и 1 + |x_n0|. Для данного М будет выполнено условие: |x_n| < M, что и требовалось доказать.

Определение. Последовательность называется стационарной, если все её члены равны между собой. Стационарная последовательность является простейшим примером фундаментальной последовательности.

Определение. Упорядоченное поле называется Архимедовски упорядоченным, если для любого элемента а данного поля и любого элемента данного поля b > 0, существует такое натуральное число n, что

а < bn.

Аксиоматически множество действительных чисел определяется как Архимедовски упорядоченное поле, которое обладает свойством полноты (то есть любая фундаментальная последовательность в этом поле сходится). Эта аксиоматическая теория была построена Ш. Мерэ (1869) и Г. Кантором (1871). Поле действительных чисел обозначается символом R.

Моделью множества действительных чисел служит множество классов фундаментальных последовательностей рациональных чисел (две последовательности принадлежат к одному классу, если разность между соответствующими членами последовательности является бесконечно малой последовательностью, то есть последовательностью сходящейся к нулю – это отношение эквивалентности также называют конфинальностью последовательностей).

Операция сложения фундаментальных последовательностей может быть задана по следующему правилу: суммой двух фундаментальных последовательностей (а_n) + (b_n) называется последовательность, все элементы которой есть суммы соответствующих элементов из складываемых последовательностей, то есть

(а_n) + (b_n) = (а_n + b_n).

Теорема 4. Сумма фундаментальных последовательностей есть снова последовательность фундаментальная.

Доказательство: Если последовательность фундаментальна, то для любого e/2 > 0 существует такой номер n₀, что модуль разности между любыми двумя членами данной последовательности с номерами, большими, чем n₀, будет меньше, чем e/2. Таким образом, |a_n – a_m| < ε/2, |b_n – b_m| < ε/2. Тогда,

|a_n + b_n – (a_m + b_m)| £ |a_n – a_m| + |b_n – b_m| < ε/2 + ε/2 < ε,

что справедливо при любом ε, поэтому сумма является последовательностью фундаментальной.

Аналогично вводятся понятия разности и произведения фундаментальных последовательностей. Доказательство теоремы о том, что разность фундаментальных последовательностей снова является последовательностью фундаментальной, в точности повторяет доказательство соответствующей теоремы для суммы последовательностей. Докажем теорему для умножения.

Теорема 5. Произведение фундаментальных последовательностей есть снова последовательность фундаментальная.

Доказательство: Если последовательность фундаментальна, то она ограничена. Пусть последовательность (а_n) ограничена числом М₁, а последовательность (b_n) числом М₂. Тогда в качестве e₁ выберем min { , 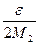} и найдём такой номер, что (|a_n – a_m| < ε₁, |b_n – b_m| < ε₁). Тогда,

|a_n b_n – a_mb_m| =|a_n b_n – a_mb_n + a_mb_n – a_mb_m| ≤ |a_n – a_m|×|b_n|+ |b_n – b_m| |a_n| < ε/2 + ε/2 < ε,

что справедливо при любом ε, а значит произведение является последовательностью фундаментальной.

Для классов эквивалентных между собой фундаментальных последовательностей определения операций вводятся аналогично.

Для доказательства того, что полученное множество классов фундаментальных последовательностей является полем, непосредственно проверяются все законы (они справедливы для рациональных чисел, а значит и для составленных из них фундаментальных последовательностей). Последовательность называется нулевой, если все её члены сколь угодно малы по модулю (последовательность является бесконечно малой), то есть для любого ε, начиная с некоторого номера, |a_n| < ε. Отметим также, что сумма двух нулевых последовательностей есть последовательность нулевая, и произведение нулевой последовательности на любую фундаментальную последовательность также есть последовательность нулевая. Нулевая последовательность всегда является фундаментальной (так как она сходится к нулю, то есть имеет предел).

Интерес представляет доказательство того, что обратный элемент для любой ненулевой фундаментальной последовательности существует. Здесь необходимо ввести понятия положительной и отрицательной последовательности.

Определение. Последовательность называется положительной, если существует такое положительное число К и такой натуральный номер, что все члены последовательности начиная с данного номера будут больше, чем К. Последовательность называется отрицательной, если противоположная ей последовательность положительна.

Теорема 6. Всякая фундаментальная последовательность является либо положительной, либо отрицательной, либо нулевой.

Доказательство: Докажем в начале, что если последовательность не является нулевой, то существует положительное число К, такое, что |a_n| > K.

Действительно, последовательность фундаментальна, то есть |a_m – a_n| < e для всех номеров, больших чем n₀. Предположим, что теорема не верна, то есть для любого положительного e существуют сколь угодно большие номера (в том числе и большие n₀), такие, что члены последовательности |а_n| < e. Фиксируем один из них. Так как последовательность фундаментальна, при номерах, больших чем n₀

|a_m| – |a_n| £ |a_m – a_n| < e

|a_m| < e + |a_n| < e + e. Последнее означает, что все члены, начиная с некоторого номера n₀, по модулю являются сколь угодно малыми, а это означает, что данная последовательность нулевая, что противоречит условию. Таким образом, для ненулевой фундаментальной последовательности существует положительное число К, такое, что |a_n| > K. Тогда, либо а_n > K, либо – а_n > K. В силу фундаментальности последовательность для достаточно больших номеров оба условия одновременно выполняться не могут. Действительно, если например, a_n > K, и –a_m > K, то

|a_m – a_n| £ |a_m| + |– a_n| = –a_m + a_n > K + K,

что противоречит фундаментальности (a_n). Таким образом, любая не сходящаяся к нулю фундаментальная последовательность является либо положительной, либо отрицательной.

Если теперь последовательность (a_n) отлична от нулевой, докажем, что для неё имеется обратная. Действительно, если последовательность не является нулевой, то она может иметь разве лишь конечное число нулевых членов. На соответствующих нулям позициях для обратной последовательности также будем записывать нули. Для остальных членов последовательности в соответствующих позициях будем записывать обратные им элементы, то есть 1/а_n. При умножении полученной последовательности на исходную, получим последовательность, имеющую разве лишь конечное число нулевых членов, а все остальные челны произведения будут равны 1. Такая последовательность имеет предел, равный 1, а, следовательно, является фундаментальной единичной последовательностью (эквивалентной стационарной последовательности равной единице. Докажем, что построенная обратная последовательность также является фундаментальной. Действительно,

= =

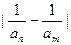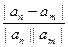
Так как последовательность не является нулевой, начиная с некоторого номера,

|a_n| > d.

= < .

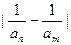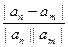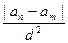Так как последовательность (a_n) фундаментальна, можно также считать, что

|a_n – a_m| < ed², то есть 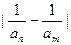< e.

Теперь докажем, что построенное поле является упорядоченным. Для этого проверим справедливость условий из определения расположенного кольца. Во-первых, будем считать, что фундаментальная последовательность больше нуля, если она положительна. По теореме 6, всякая фундаментальная последовательность является либо положительной (большей нуля), либо отрицательной (противоположная к ней положительна), либо нулевой. Кроме того, если (а_n) > 0, (b_n) > 0, то начиная с некоторого номера n₀: a_n > K₁ > 0, и начиная в некоторого номера n₁: b_n > K₂ > 0. Выберем n₂ = mах{n₀, n₁}. Тогда для всех номеров больших, чем n₂

a_n + b_n > K₁ + K₂, a_n ×b_n > K₁×K₂ (в силу справедливости свойств монотонности для рациональных чисел), а значит сумма и произведение положительных последовательностей снова будут последовательностями положительными.

Теорема 7 (об Архимедовской упорядоченности). Для любой фундаментальной последовательности (а_n) рациональных чисел, а также для любой положительной фундаментальной последовательности рациональных чисел (b_n)>0 существует такое натуральное число k, что при всех достаточно больших номерах n выполняется условие:

a_n < kb_n или (kb_n – a_n) > 0.

Доказательство: Так как (b_n) > 0, существует такое рациональное число d > 0, что для всех достаточно больших номеров b_n > d. С другой стороны (а_n) – фундаментальная, а значит ограниченная, то есть а_n < |a_n| < M, где М – также рациональное число. Для рациональных чисел теорема Архимеда выполняется, то есть существует натуральное k такое, что М < kd => a_n < M <kd < kb_n для достаточно больших номеров, а значит

kb_n – a_n > kd – M,

то есть последовательность (kb_n – a_n) > 0, что и требовалось доказать.

Все теоремы о сравнениях фундаментальных последовательностей легко обобщаются на классы конфинальных фундаментальных последовательностей. Для этого достаточно доказать, что если фундаментальная последовательность положительна, то и эквивалентная ей также будет положительна (доказательство по существу аналогично теореме 6). Таким образом, множество классов эквивалентных фундаментальных последовательностей рациональных чисел есть Архимедовски упорядоченное поле. Если теперь мы поставим в соответствие сходящимся последовательностям их рациональные пределы, а всем остальным фундаментальным последовательностям – некоторые новые символы, которые будут являться иррациональными числами, то мы получим модель поля действительных чисел. Остаётся доказать лишь свойство полноты построенного множества, то есть то, что каждая последовательность состоящая из действительных (а не только рациональных!) чисел имеет предел. Для этого предварительно докажем следующую теорему.

Теорема 8. Для любого действительного числа a и для любого рационального e > 0, существует такое рациональное число r, что |a – r| < e.

Доказательство: Так как a – действительное число, следовательно, оно либо рационально, (тогда оно совпадает с искомым), либо иррационально, то есть существует фундаментальная последовательность, сходящаяся к a: для любого рационального числа e₁ = e/2 можно найти номер n₀, что для всех достаточно больших номеров n >n₀: |a_n – a_n0| < e/2. Рассмотрим стационарную последовательность, состоящую из r = a_n0, а также стационарную последовательность, состоящую из e. Разность a – r = (a_n) – (a_n0) меньше последовательности, состоящей из e. Действительно, e – |a – r| = e – |a_n – a_n0| > e – e/2 = e/2.

Теорема 9. Любая фундаментальная последовательность, составленная из классов фундаментальных последовательностей рациональных чисел, сходится (модель обладает свойством полноты).

Доказательство: Пусть (a_n) – фундаментальная последовательность действительных чисел (как пределов некоторых фундаментальных последовательностей рациональных чисел). Тогда для любого числа a_n существует сколь угодно близкое к нему рациональное число r_n. Выберем эти числа так, чтобы выполнялись неравенства:

|a₁ – r₁| < 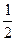, |a₂ – r₂| < 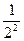… |a_р – r_р| < …

Последовательность рациональных чисел (r_n) также является фундаментальной. Действительно, подберём такое значение p, чтобы < < 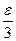и

|a_n+p – a_p| < 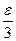(такое значение р существует в силу того, что (a_n) фундаментальна). Тогда

|r_n+p – r_n| = |r_n+p – a_n+p + a_n+p – a_p+ a_p – r_n| £ |r_n+p – a_n+p| + |a_n+p – a_p|+ |a_p – r_n| <

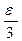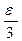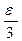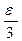< + + < + + < e. Таким образом, последовательность рациональных числе (r_n) сходится к некоторому действительному числу a. Данное a является также и пределом исходной последовательности действительных чисел. Выберем n₀ так, чтобы |r_n – a| < e/2 (существует в силу определения предела) и |a_n – r_n| < e/2 (существует по построению чисел r_n). Тогда при всех номерах больших выбранного

|a_n – a| = |a_n – r_n + r_n –a_n| £ |a_n – r_n| + |r_n – a| < e/2 + e/2 < e,

что и требовалось доказать.

Таким образом, модель действительных чисел построена и аксиоматическая теория действительных чисел непротиворечива.

Помимо рассмотренного выше подхода к построению аксиоматической теории действительных чисел по Мере-Кантору, существует и целый ряд других подходов, например, теория К. Вейерштрасса (1865), Р. Дедекинда (1872) и другие.

Задания для самостоятельного решения

№3.1. Доказать, что число иррационально:

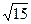а) ; б) ; в) 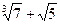; г) log₇6; д)сos 10⁰; е) tg 5⁰;

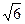ж) ; з) ; з) 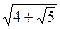; и) log₂3; к) сos 20⁰; л) сtg 10⁰.

№ 3.2. Упростите выражение:

а) ;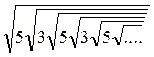

б)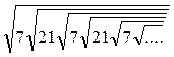

№ 3.3. Решите уравнение:

= 49.