 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Упорядоченность множества натуральных чисел. Неравенства на множестве натуральных чисел
|
|
Будем говорить, что натуральное число а больше, чем натуральное число b (и обозначать а > b), если существует такое натуральное k, что а = b + k.
Теорема 1. Единица не больше никакого натурального числа.
Действительно, условие 1 > a влечёт за собой 1 = а + k, что невозможно: для k = 1 получим 1 = а/, что противоречит первой аксиоме натуральных чисел; для k ¹ 1 найдём для него предшествующий и вновь придем к тому же противоречию.
Данное отношение «больше» является антирефлексивным (не верно, что а > a) и транзитивным (а > b /\ b > c => a > c), то есть является отношением строгого порядка. Более того, данное отношение является отношением линейного порядка, то есть для множества натуральных чисел справедлива теорема о трихотомии:
Теорема о трихотомии: Для любых двух натуральных чисел справедливо одно и только одно из следующих трёх утверждений:
1) а > b
2) b > a
3) a = b.
Доказательство: Вначале покажем, что никакие два из трёх условий не выполняются одновременно. Допустим, что выполнены условия 1 и 2. Тогда
a = b + k, b = a + n => a = a + (n + k) => a > a,
что противоречит антирефлексивности отношения «больше». Аналогично устанавливается несовместность условий 2 и 3, условий 1 и 3.
Теперь докажем, что одно из трёх условий обязательно имеет место для любых чисел а и b. Используем математическую индукцию по b. При b = 1, в зависимости от а: либо а = 1 = b, либо для а имеется предшествующий, тогда
а = с/ = с + 1 = 1 + с = b + c => a > b.
Таким образом, для b = 1 утверждение теоремы справедливо. Сделаем индукционное предположение о том, что теорема справедлива для некоторого х, а именно, что х сравним с числом а, то есть возможны три варианта: либо a > x, либо x > a, либо х = а. Тогда докажем, что и х/ также сравним с а. В первом случае a > x, то есть а = х + k. В зависимости от того, будет данное k равно 1 или нет, получим
а) а = х + 1 = х/ (теорема справедлива)
б) а = х + с/ = х + с + 1 = х + 1 + с = х/ + с => a > x/.
Во втором случае x > a, но тогда
х = а + m,
х/ = (а + m) +1 = a + (m + 1),
то есть x/ > a. Аналогично при х = а, х/ = х + 1 = а + 1, то есть снова x/ > a. Теорема полностью доказана.
Теперь можно ввести понятия <, £, ³.
a < b ó b > a;
a £ b ó a < b \/ a = b
a ³ b ó a > b \/ a = b.
Свойства монотонности:
Для операции сложения:
1) а > b => a + c > b + c;
2) a + c > b + c => а > b;
3) а > b /\ c > d=> a + c > b + d.
Те же свойства имеют место и для других знаков <, £, ³.
Для операции умножения:
4) а > b => a×c > b×c;
5) Закон сокращения: ас = bc => a = b
6) ac > bc => а > b;
7) а > b /\ c > d=> ac > bd.
Те же свойства имеют место и для других знаков <, £, ³.
Приведём в качестве примера доказательства свойств 4 и 5. Так как а > b, по определению а = b + k, тогда а×с = (b + k)×c = b×c + k×c, что означает, что a×c > b×c, и свойство 4 доказано. Свойство 5 докажем методом от противного. Пусть ас = bc, но предположим, что а ≠ b, но тогда, по теореме о трихотомии, либо а > b, либо b > a, но это означает, согласно свойству 4, что либо ас > bс, либо bс > aс, что противоречит условию (ас = bc).
Теорема о дискретности. Между двумя соседними натуральными числами нельзя вставить натуральное число:
(" а, х Î N) не верно, что а < x < a/
Доказательство (методом от противного). Пусть а < x < a/. Тогда х = а + k,
a/ = x + n = a + k + n => a + 1 = a + k + n => 1 = k + n.
Последнее равенство невозможно, так как противоречит теореме о том, что единица не больше никакого натурального числа.
Терема Архимеда. Для любых натуральных чисел а и b существует такое натуральное n, что a < bn.
Доказательство проведём индукцией по b. Для b = 1, n = a/. Сделаем индукционное предположение, что для b = k требуемое n существует, то есть a < kn. Но тогда тем более a < k/n = kn + k. Теорема доказана.
Наименьшим элементом множества М будем называть такой элемент с Î М, что для любых элементов m Î M выполнено неравенство: с ≤ m.
Теорема о наименьшем элементе. Любое непустое подмножество множества натуральных чисел имеет наименьший элемент.
Доказательство: Если М – подмножество N, содержащее в себе 1, то 1 как раз и будет искомым наименьшим элементом. Если же 1 не входит в множество М, то рассмотрим вспомогательное множество А, состоящее из всех натуральных чисел меньших, чем все натуральные числа из множества М:
А = {a Î N | (" m Î M) a < m}.
Из этого построения, в частности следует, что множества А и М не имеют общих элементов. Кроме того, А – не пусто, так как 1 Î А. В А есть также элемент b, что b/ Ï А. Действительно, если бы такого элемента не было, то по аксиоме индукции можно было бы доказать, что А = N, но тогда М было бы пусто, что не соответствует условию теоремы. Элемент b/ = с как раз и будет наименьшим элементом во множестве М. Действительно, с £ m для любого m ÎМ (если бы это было не так, то неравенство с > m выполнялось бы хотя бы при одном натуральном m, но b Î A, поэтому b < m < c = b/, что противоречит теореме о дискретности). Кроме того, с не может быть строго меньше всех элементов множества М, иначе с Î А, что противоречит его выбору. Таким образом, с равен хотя бы одному элементу из М, а значит с Î М, то есть действительно с – наименьший элемент множества М. Теорема доказана.
Заметим, что не всякое подмножество множества натуральных чисел имеет наибольший элемент, но если это подмножество конечно, то в нём имеется и наибольший элемент. Верно и обратное. Если подмножество множества натуральных чисел имеет наибольший элемент, то это подмножество конечно. Можно доказать даже более общее утверждение: непустое подмножество множества натуральных чисел ограничено сверху тогда и только тогда, когда оно конечно (имеет наибольший элемент).
Задания для самостоятельного решения
№ 1.8. Докажите антирефлексивность и транзитивность отношения «больше» на множестве натуральных чисел.
№ 1.9. Докажите свойства монотонности 1, 2, 3, 6, 7 из данного параграфа.
№ 1.10. Докажите неравенства для всех натуральных n
а) 5n > 7n – 3;
б) 2n+2 > 2n + 5;
в) 2n+2 > n2 + 2;
г) 2n > n;
д) 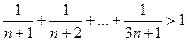 .
.
Дата публикования: 2015-09-17; Прочитано: 1518 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
