Аксиоматическое определение натуральных чисел

При построении аксиоматической теории натуральных чисел первичными терминами будут являться «элемент» или «число» (которые в контексте данного пособия мы можем рассматривать как синонимы) и «множество», основными отношениями: «принадлежность» (элемент принадлежит множеству), «равенство» и «следовать за», обозначаемое а^/ (читается «число а штрих следует за числом а», например, за двойкой следует тройка, то есть 2^/ = 3, за числом 10 следует число 11, то есть 10^/ = 11 и т.д).

Множеством натуральных чисел (натуральным рядом, положительными целыми числами) называется множество N с введённым отношением «следовать за», в котором выполнены следующие 4 аксиомы:

А₁. Во множестве N существует элемент, называемый единицей, который не следует ни за каким другим числом.

А₂. Для каждого элемента натурального ряда существует единственный следующий за ним.

А₃. Каждый элемент N следует не более чем за одним элементом натурального ряда.

А₄. (Аксиома индукции) Ели подмножество М множества N содержит в себе единицу, а также вместе с каждым своим элементом а содержит и следующий за ним элемент а^/, то М совпадает N.

Те же аксиомы можно записать кратко с помощью математических символов:

А₁ ($ 1 Î N) (" a Î N) a^/ ≠ 1

A₂ (" a Î N) ($ a^/ Î N) a = b => a^/ = b^/

A₃ a^/ = b^/ => a = b

A₄

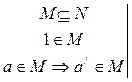=> М = N

Если элемент b следует за элементом а (b = а^/), то будем говорить, что элемент а является предшествующим для элемента b (или предшествует b). Данная система аксиом носит название системы аксиом Пеано (так как была введена в XIX веке итальянским математиком Джузеппе Пеано). Это лишь один из возможных наборов аксиом, позволяющий определить множество натуральных чисел; существуют и другие эквивалентные подходы.

Простейшие свойства натуральных чисел

Свойство 1. Если элементы различны, то и следующие за ними различны, то есть

a ¹ b => a^/ ¹ b^/.

Доказательство осуществляется методом от противного: предположим, что a^/ = b^/, тогда (по А₃) a = b, что противоречит условию теоремы.

Свойство 2. Если элементы различны, то и предшествующие им (если они существуют) различны, то есть

a^/ ¹ b^/ => a ¹ b.

Доказательство: предположим, что a = b, тогда, согласно А₂ имеем a^/ = b^/, что противоречит условию теоремы.

Свойство 3. Никакое натуральное число не равно следующему за ним.

Доказательство: Введём в рассмотрение множество М, состоящее из таких натуральных чисел, для которых данное условие выполняется

М = {a Î N | a ¹ a^/}.

Доказательство будем проводить, опираясь на аксиому индукции. По определению множества М, оно является подмножеством множества натуральных чисел. Далее 1ÎМ, так как единица не следует ни за каким натуральным числом (А₁), а значит в том числе и для а = 1 имеем: 1 ¹ 1^/. Предположим теперь, что некоторое а Î М. Это означает, что a ¹ a^/ (по определению М), откуда a^/ ¹ (a^/)^/ (свойство 1), то есть a^/ Î М. Из всего выше сказанного на основании аксиомы индукции можно заключить, что М = N, то есть наша теорема верна для всех натуральных чисел.

Теорема 4. Для любого натурального числа отличного от 1 существует предшествующее ему число.

Доказательство: Рассмотрим множество

М = {1} È {c ÎN | ($ a Î N) c = a^/}.

Данное М есть подмножество множества натуральных чисел, единица явно принадлежит данному множеству. Вторая же часть этого множества – это элементы, для которых существуют предшествующие, следовательно, если а Î М, то a^/ тоже принадлежит М (его второй части, так как у a^/ есть предшествующий – это а). Таким образом, на основании аксиомы индукции М совпадает с множеством всех натуральных чисел, а значит все натуральные числа это либо 1, либо те, для которых существует предшествующий элемент. Теорема доказана.

Непротиворечивость аксиоматической теории натуральных чисел

В качестве интуитивной модели множества натуральных чисел можно рассматривать наборы чёрточек: числу 1 будет соответствовать |, числу 2 ||, и т.д., то есть натуральный ряд будет иметь вид:

|, ||,

,

Данные ряды чёрточек могут служить моделью натуральных чисел, если в качестве отношения «следовать за» использовать «приписывание одной чёрточки к числу». Справедливость всех аксиом является интуитивно очевидной. Разумеется, данная модель не является строго логической. Для построения строгой модели нужно иметь другую заведомо непротиворечивую аксиоматическую теорию. Но такой теории в нашем распоряжении, как уже отмечалось выше, нет. Таким образом, либо мы вынуждены опереться на интуицию, либо не прибегать к методу моделей, а сослаться на то, что на протяжении более чем 6 тысячелетий, во время которых осуществляется изучение натуральных чисел, никаких противоречий с данными аксиомами обнаружено не было. Независимость системы аксиом Пеано Для доказательства независимости первой аксиомы достаточно построить модель, в которой аксиома А1 ложна, а аксиомы А2, А3, А4 истины. Рассмотрим в качестве первичных терминов (элементов) числа 1, 2, 3, а отношение «следовать за» определим соотношениями: 1/ = 2, 2/ = 3, 3/ = 1. В этой модели нет элемента, который бы не следовал ни за каким другим (аксиома 1 ложна), но все остальные аксиомы выполняются. Таким образом, первая аксиома не зависит от остальных. Вторая аксиома состоит из двух частей – существования и единственности. Независимость данной аксиомы (в части существования) можно проиллюстрировать на модели из двух чисел {1, 2} с отношением «следовать за», заданным единственным соотношением: 1/ = 2: Для двойки отсутствует следующий элемент, аксиомы же А1, А3, А4 истинны. Независимость данной аксиомы, в части единственности, иллюстрирует модель, в которой множеством N будет множество всех обычных натуральных чисел, а также всевозможных слов (наборов букв, не обязательно имеющих смысл), составленных из букв латинского алфавита (после буквы z следующей будет аа, затем аb … аz, затем ba …; за всеми возможными словами из двух букв, последним из которых будет zz, последует слово ааа, и так далее). Отношение «следовать за» введём так, как показано на рисунке: Здесь аксиомы А1, А3, А4 также истинны, но за 1 следует сразу два элемента 2 и а. Таким образом, аксиома 2 не зависит от остальных. Независимость аксиомы 3 иллюстрирует модель: в которой А1, А2, А4 истинны, но число 2 следует и за числом 4, и за числом 1. Для доказательства независимости аксиомы индукции используем множество N, состоящее из всех натуральных чисел, а также трёх букв {a, b, c}. Отношение следования в данной модели можно ввести так, как показано на следующем рисунке: Здесь для натуральных чисел используется обычное отношение следования, а для букв отношение «следовать за» определяется следующими формулами: a/ = b, b/ = c, c/ = a. Очевидно, что 1 не следует ни за каким натуральным числом, для каждого имеется следующий, и притом только один, каждый элемент следует не более чем за одним элементом. Однако если мы рассмотрим множество М состоящее из обычных натуральных чисел, то это будет подмножество данного множества, содержащее единицу, а также следующий элемент для каждого элемента из М. Однако это подмножество не будет совпадать со всей рассматриваемой моделью, так как не будет содержать в себе буквы a, b, c. Таким образом, аксиома индукции в данной модели не выполняется, а, следовательно, аксиома индукции не зависит от остальных аксиом. Аксиоматическая теория натуральных чисел является категоричной (полной в узком смысле). Для доказательства категоричности достаточно ввести изоморфизм для любых двух моделей натуральных чисел. Такой изоморфизм можно построить для натуральных чисел исходя из условий: j(1) = 1 j (n/) =(j (n)) /. Принцип полной математической индукции. Теорема индукции. Пусть некоторое утверждение Р(n) сформулировано для всех натуральных чисел, и пусть а) Р(1) – истинно, б) из того, что Р(k) истинно, следует, что Р(k/) также истинно. Тогда утверждение Р(n) справедливо для всех натуральных чисел. Для доказательства введём множество М таких натуральных чисел n (М Í N), для которых утверждение Р(n) истинно. Воспользуемся аксиомой A4, то есть попытаемся доказать, что: 1) 1 Î М; 2) k Î M => k/ Î M. Если нам это удастся, то, согласно аксиоме А4, мы сможем сделать вывод, что M = N, то есть P(n) истинно для всех натуральных числе. 1) По условию а) теоремы, Р(1) истинно, следовательно, 1 Î М. 2) Если некоторое k Î М, то (по построению М) Р(k) – истинно. По условию б) теоремы, это влечёт за собой истинность Р(k/), а значит k/ Î М. Таким образом, по аксиоме индукции (А4) М = N, а значит Р(n) истинно для всех натуральных чисел. Таким образом, аксиома индукции позволяет создать метод доказательства теорем «по индукции». Данный метод играет ключевую роль при доказательстве основных теорем арифметики, касающихся натуральных чисел. Он состоит в следующем: 1) проверяется справедливость утверждения для n=1 (база индукции), 2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число (индукционное предположение), и с учётом этого предположения устанавливается справедливость утверждения для n=k/ (индукционный шаг). Доказательство, основанное на данном алгоритме, называется доказательством методом математической индукции.   Задания для самостоятельного решения № 1.1. Выяснить, какие из перечисленных систем удовлетворяют аксиомам Пеано (являются моделями множества натуральных чисел), определить, какие аксиомы выполнены, а какие – нет. а) N ={3, 4, 5 …}, n/ = n + 1; б) N ={n ³ 6, n Î N}, n/ = n + 1; в) N ={n ³ – 2, n Î Z}, n/ = n + 1; г) N ={n ³ – 2, n Î Z}, n/ = n + 2; д) нечётные натуральные числа, n/ = n +1; е) нечётные натуральные числа, n/ = n +2; ж) Натуральные числа с отношением n/ = n + 2; з) N ={1, 2, 3}, 1/ = 3, 2/ = 3, 3/ = 2; и) N ={1, 2, 3, 4, 5}, 1/ = 2, 2/ = 3, 3/ = 4, 4/ = 5, 5/ = 1; к) Натуральные числа, кратные 3 с отношением n/ = n + 3 л) Чётные натуральные числа с отношением n/ = n + 2 м) Целые числа,.