Пример 2.18

.

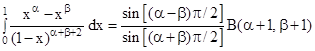
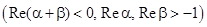Отсюда следует, что ,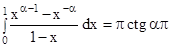

.

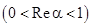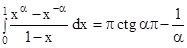
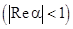Пример 2.19.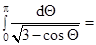

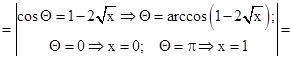
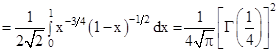
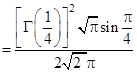
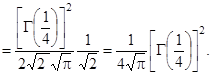
Пример 2.20. Вычислим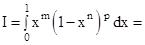

.

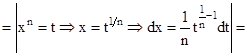
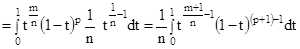
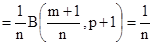
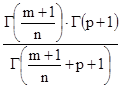Напомним, что интеграл от дифференциального бинома 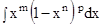выражается в конечном виде только в трех случаях, когда одно из чисел p, 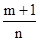, 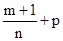- целое. Посмотрим, что дают эти случаи применительно к интегралу

1. Если p – целое, то

-

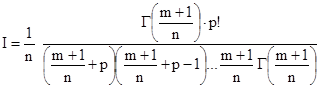не содержит гамма-функцию.

2. Если 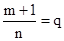- целое, то

-

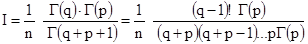не содержит гамма-функцию.

3. Если 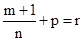- целое, то

-

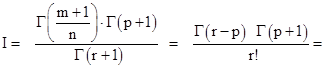
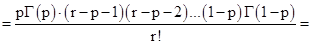
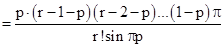также не содержит гамма-функцию – полная аналогия с результатом Чебышева.

2.2. Свойства бета–функции

1. Из формулы следует, что

.

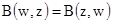2. ,

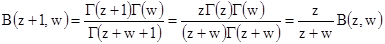т.е.

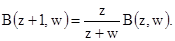
3. При 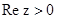рассмотрим

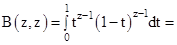
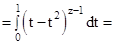(см. рис. 2.3)

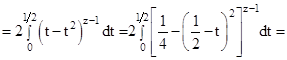
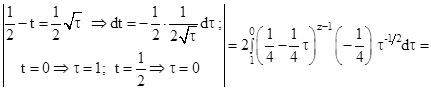
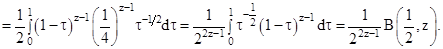
Таким образом доказано, что при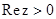

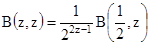, следовательно, в силу аналитического продолжения эта формула справедлива .

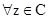Следствие. Записав бета-функцию через гамма, получим:

.

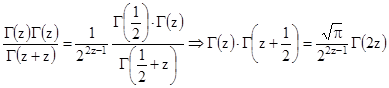Последняя формула носит название формулы удвоения (или формулы Лежандра). Перепишем ее так:

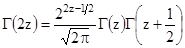. (2.4)

Можно доказать, что справедливы также формула утроения

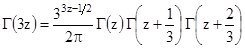, (2.5)

а также общая формула умножения Гаусса-Лежандра

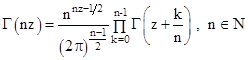. (2.6).

Пользуясь этой формулой, легко найти так называемое произведение Эйлера

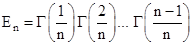. (2.7)

Действительно,

.

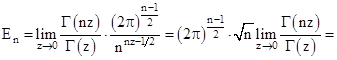
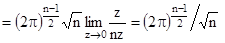Заметим, что для 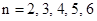величину 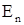можно легко найтинепосредственно. А именно, ;

;

;

;

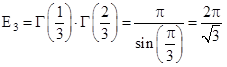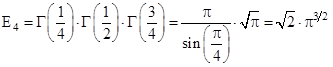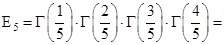
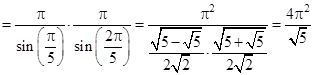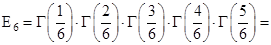
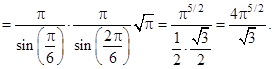
Отметим еще, что произведение Эйлера можно найти и без привлечения общей формулы умножения. А именно, перемножая два равенства

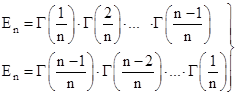
почленно и пользуясь формулой дополнения

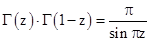, получаем

.

Для вычисления произведения синусов в знаменателе представим каждый из них по формуле Эйлера:

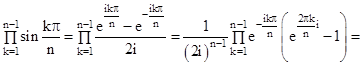
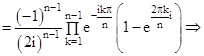
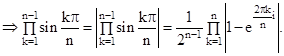
Но 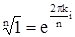, 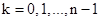. Следовательно,

.

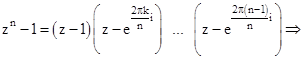
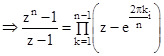Устремляя здесь 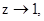получаем 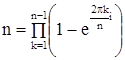, откуда .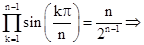

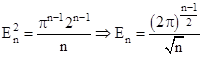Проверка. 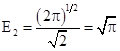(истина);

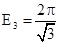(истина);

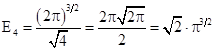(истина);

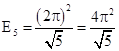(истина);

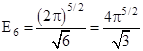(истина).