Приведение кривых второго порядка к каноническому виду

Общее уравнение кривой второго порядка имеет вид:

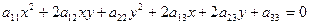. (9.16)

Для приведения уравнения (9.16) к каноническому виду нужно, чтобы коэффициенты приняли нулевые значения. Этого можно добиться за счёт переноса начала координат и поворота системы координат.

При переносе начала координат в точку 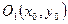соотношения между старыми и новыми координатами имеют следующий вид:

(9.17)

При повороте осей на угол :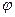

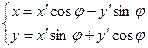(9.18)

Смысл обозначений и 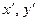очевиден из соотношений (9.17) и (9.18).

Подставив (9.17) в уравнение (9.16), получим:

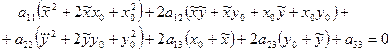
Перегруппируем члены уравнения:

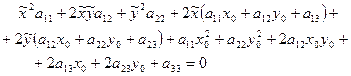(9.19)

Выберем 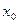и 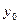так, чтобы коэффициенты при и 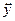обратились в нуль. Для этого решим следующую систему уравнений:

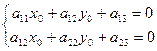(9.20)

Решение системы существует только в случае

,

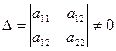поэтому начинать следует с вычисления значения .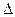

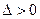( для эллипса, для гиперболы, 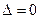для параболы.)

Последнее обстоятельство заставляет начинать преобразование уравнения параболы с поворота осей координат.

Из выражения (9.19) очевидно, что коэффициенты при старших степенях 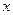и 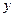при переносе начала координат не изменяются. Последние шесть членов выражения (9.19) перегруппируем следующим образом:

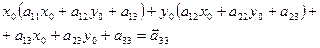(9.21)

Содержимое круглых скобок в соответствии с (9.21) обращается в нуль, а три оставшиеся члена выражения позволяют найти новое значение свободного члена 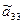преобразованного уравнения кривой.

В итоге, уравнение (9.16) приобретает следующий вид:

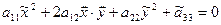(9.22)

Кривая, описываемая этим уравнением симметрична относительно центра, так как выполняется условие

.

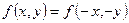Очевидно, что центр симметрии кривой это точка .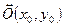

Поворот системы координат вокруг центра симметрии кривой позволяет избавиться от перекрестного члена уравнения (9.22).

Подставив в уравнение (9.22) соотношения (9.18) и перегруппировав члены полученного выражения, из условия обращения в нуль коэффициента при перекрестном члене, получим следующее соотношение:

.

Разделив его на 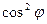получим квадратное уравнение для :

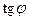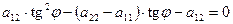. (9.23)

Это уравнение имеет два решения: 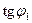и 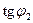, причём .

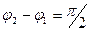Существуют три инварианта для уравнения (9.16), значения которых не изменяются при преобразованиях декартовой системы координат.

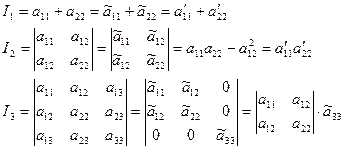(9.24)

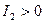для эллипса, 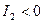для гиперболы, 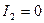для параболы.

Используя инварианты, уравнение (9.22) можно записать так:

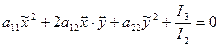(9.25)

Решая примеры, убедимся, что использование инвариантов существенно упрощает приведение уравнений кривых второго порядка к каноническому виду