 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прямая линия в трехмерном пространстве
|
|
Прямую линию в пространстве можно определить как линию пересечения двух непараллельных плоскостей.
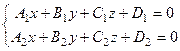 . (7.1)
. (7.1)
Часто удобнее канонический вид уравнения прямой.
Определение 7.1. Любой ненулевой вектор 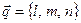 , параллельный данной прямой будем называть направляющим вектором прямой.
, параллельный данной прямой будем называть направляющим вектором прямой.
Задача 7.1. Составить уравнение прямой 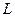 , проходящей через точку
, проходящей через точку 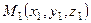 параллельно вектору
параллельно вектору 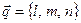 .
.

Решение.
Рассмотрим вектор 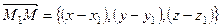 , начало которого совпадает с точкой
, начало которого совпадает с точкой 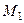 , а конец − в произвольной точке
, а конец − в произвольной точке 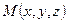 .
.
Чтобы точка 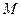 лежала на прямой
лежала на прямой 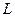 , вектор
, вектор 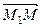 должен быть параллелен вектору
должен быть параллелен вектору 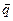 . Условие параллельности векторов состоит в пропорциональности сходственных координат, из чего следует
. Условие параллельности векторов состоит в пропорциональности сходственных координат, из чего следует
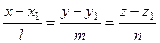 (7.2)
(7.2)
Это уравнение называется каноническим уравнением прямой в пространстве.
Приравняв выражение (7.2) параметру 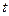 , получим параметрические уравнения прямой.
, получим параметрические уравнения прямой.
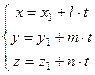 (7.3)
(7.3)
Эти уравнения имеют наглядное физическое истолкование. Если принять что, 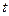 −время, а
−время, а 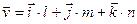 вектор скорости, то уравнения (7.3) − это три проекции уравнения движения точки на координатные оси.
вектор скорости, то уравнения (7.3) − это три проекции уравнения движения точки на координатные оси.
Уравнение прямой, проходящей через две заданные точки 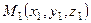 и
и 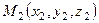 получим из уравнения (7.2), приняв, что направляющий вектор
получим из уравнения (7.2), приняв, что направляющий вектор
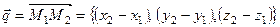 (7.4)
(7.4)
и подставив выражение (7.4) в (7.2):
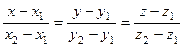 (7.5)
(7.5)
Чтобы привести к каноническому виду уравнение прямой, заданной как линия пересечения двух плоскостей, нужно найти направляющий вектор прямой и точку, лежащую на прямой. Длина вектора − произвольная, точка, лежащая на прямой − любая.
Пусть прямая есть линия пересечения плоскостей (7.6)
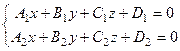 . (7.6)
. (7.6)
Направляющий вектор прямой 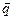 ортогонален каждому из нармальных векторов плоскостей
ортогонален каждому из нармальных векторов плоскостей
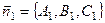 и
и 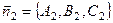 .
.
Поэтому определим вектор 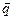 , как векторное произведение нормальных векторов
, как векторное произведение нормальных векторов
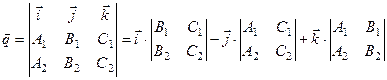 (7.7)
(7.7)
Компоненты вектора 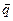 будут иметь вид
будут иметь вид
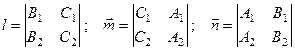 (7.8)
(7.8)
Для определения координат точки, лежащей на прямой, добавим в систему уравнений (7.6) уравнение третьей плоскости. Удобно добавить одну из координатных плоскостей 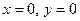 или
или 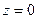 .
.
Чтобы получающаяся система уравнений второго порядка имела единственное решение, её главный определитель не должен обращаться в нуль. Это накладывает ограничения на выбор координатной плоскости.
Пусть 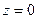 . Пусть в полученной системе уравнений
. Пусть в полученной системе уравнений
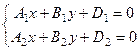 . (7.9)
. (7.9)
главный определитель 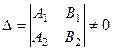 .
.
Тогда координаты искомой точки определяются по формулам Крамера
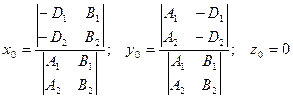 . (7.10)
. (7.10)
Искомое каноническое уравнение запишем в следующем виде
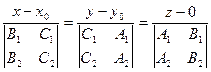 (7.11)
(7.11)
Угол между прямыми, а также условия перпенди-кулярности и параллельности прямых очевидным образом связаны с соответствующими соотношениями между их направляющими векторами 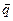 .
.
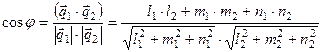 . (7.12)
. (7.12)
Условие перпендикулярности двух прямых:
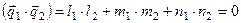 . (7.13)
. (7.13)
Условия параллельности прямых:
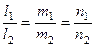 (7.14)
(7.14)
(Нуль в знаменателе в этой пропорции означает, что соответствующий числитель тоже обращается в нуль.)
Угол между плоскостью
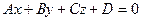 (7.15)
(7.15)
и прямой
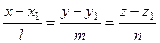 (7.16)
(7.16)
Определяется как дополнительный к углу между нормальным вектором плоскости 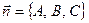 и направляющим вектором прямой
и направляющим вектором прямой 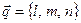 . Если угол между векторами обозначить
. Если угол между векторами обозначить 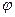 , а угол меду прямой и плоскостью
, а угол меду прямой и плоскостью 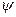 , то
, то 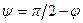 . Следовательно:
. Следовательно:
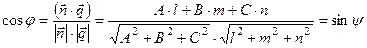 . (7.17)
. (7.17)
Условие перпендикулярности векторов 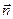 и
и 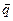
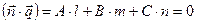 (7.18)
(7.18)
соответствует параллельности прямой и плоскости, а условие парллельности векторов 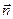 и
и 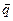
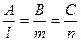 (7.19)
(7.19)
означает перпендикулярность прямой и плоскости.
Для того, чтобы прямая (7.16) принадлежала плоскости (7.15) должны быть выполнены два условия:
1. условие параллельности прямой и плоскости
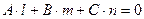 (7.20)
(7.20)
2. координаты точки 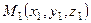 , принадлежащей прямой, должны обращать уравнение плоскости в тождество
, принадлежащей прямой, должны обращать уравнение плоскости в тождество
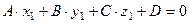 (7.21)
(7.21)
Для того, чтобы две прямые (7.22) и (7.23) принадлежали
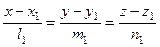 (7.22)
(7.22)
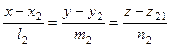 (7.23)
(7.23)
одной плоскости необходимо и достаточно, чтобы три вектора
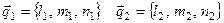 и
и
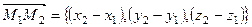
были компланарны.
Приравняв нулю смешанное произведение этих векторов, получим условие принадлежности двух прямых к одной плоскости. 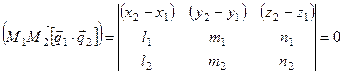 (7.24)
(7.24)
Задачи № 983, 985, 991, 1003, 1005, 1007, 1009, 1012, 1018, 1024, 1029, 1030.
Вопросы для повторения
1.Каноническое уравнение прямой в пространстве. Направляющий вектор прямой. Векторное истолкование канонического уравнения прямой. Параметрические уравнения прямой в пространстве.
2.Представление прямой, являющейся линией пересечения двух плоскостей, каноническим уравнением.
3. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
§8. Основные задачи на прямую и плоскость в пространстве
Задача 8.1.
Найти точку пересечения прямой
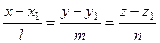 (8.1)
(8.1)
И плоскости
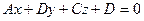 (8.2)
(8.2)
Решение.
Приравняем выражение (8.1) к параметру 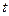 и выразим через него
и выразим через него 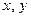 и
и 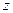
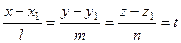 (8.3)
(8.3)
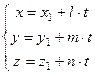 (8.4)
(8.4)
Подставим 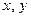 и
и 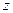 из (8.4) в уравнение плоскости.
из (8.4) в уравнение плоскости.
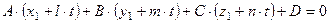 (8.5)
(8.5)
Координаты точки пересечения прямой и плоскости получим, подставив значение 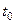 , найденное из (8.5) в уравнения (8.4).
, найденное из (8.5) в уравнения (8.4).
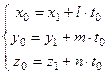 (8.6)
(8.6)
Задача 8.2.
Составить уравнение плоскости, проходящей через точку 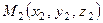 и прямую (8.7)
и прямую (8.7)
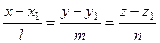 (8.7)
(8.7)
Решение.
Положение искомой плоскости определяют два вектора: направляющий вектор прямой
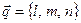
и вектор
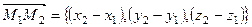 ,
,
точка начала которого 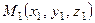 принадлежит прямой. Введем в рассмотрение «свободный вектор»
принадлежит прямой. Введем в рассмотрение «свободный вектор»
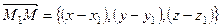 ,
,
конечная точка которого 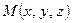 −. произвольная точка пространства.
−. произвольная точка пространства.
Чтобы эта точка принадлежала искомой плоскости, необходимо и достаточно, чтобы три рассматриваемые вектора были компланарны, а их смешанное произведение равнялось нулю. Исходя из этого, запишем уравнение искомой плоскости в матричной форме:
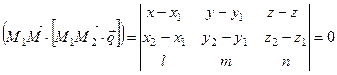 (8.8)
(8.8)
Частным случаем рассмотренной задачи является задача о плоскости, проходящей через две параллельные прямые. В этом случае точка 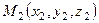 берется со второй прямой
берется со второй прямой
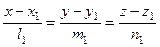 (8.9)
(8.9)
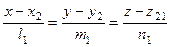 (8.10)
(8.10)
и ход решения повторяется.
Задача 8.3.
Составить уравнение плоскости, проходящей через одну из скрещивающихся прямых параллельно второй.
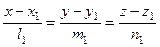 (8.11)
(8.11)
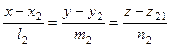 (8.12)
(8.12)
Решение.
Ориентацию в пространстве искомой плоскости определяют направляющие вектора прямых
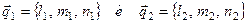
Введем в рассмотрение «свободный вектор»
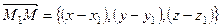 ,
,
конечная точка которого 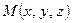 −.произвольная точка пространства, а начальная точка
−.произвольная точка пространства, а начальная точка 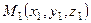 взята с первой прямой.
взята с первой прямой.
Из условия компланарности рассматриваемых векторов запишем уравнение искомой плоскости в матричной форме.
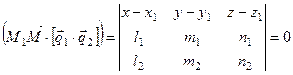 . (8.13)
. (8.13)
Задача 8.4.
Составить уравнение общего перпендикуляра двух скрещивающихся прямых
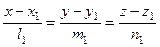 (8.14)
(8.14)
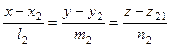 (8.15)
(8.15)
Решение.
Направляющий вектор 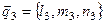 искомой прямой вычисляем как векторное произведение направляющих векторов заданных прямых
искомой прямой вычисляем как векторное произведение направляющих векторов заданных прямых
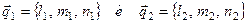
Так как по условиям задачи 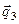 перпендикулярен
перпендикулярен 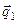 и
и 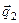 .
.
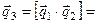
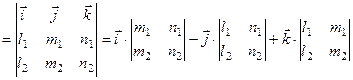 (8.16)
(8.16)
Из условия компланарности векторов 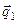 ,
, 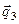 и свободного вектора
и свободного вектора
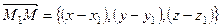 ,
,
начальная точка которого 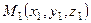 взята с первой прямой, запишем в матричной форме уравнение плоскости, проходящей через первую прямую параллельно вектору
взята с первой прямой, запишем в матричной форме уравнение плоскости, проходящей через первую прямую параллельно вектору 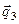 .
.
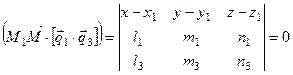 . (8.17)
. (8.17)
Аналогично, из условия компланарности векторов 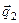 ,
, 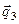 и свободного вектора
и свободного вектора
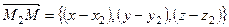 ,
,
начальная точка которого 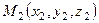 взята со второй прямой, запишем в матричной форме уравнение плоскости, проходящей через вторую прямую параллельно вектору
взята со второй прямой, запишем в матричной форме уравнение плоскости, проходящей через вторую прямую параллельно вектору 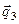 .
.
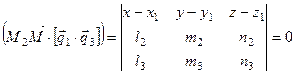 . (8.18)
. (8.18)
Линия пересечения этих плоскостей и есть искомый общий перпендикуляр.
Чтобы получить искомый общий перпендикуляр в каноническом виде можно найти точку 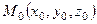 в которой пересекается вторая прямая с плоскостью (8.17). (Способ нахождения этой точки рассмотрен в задаче 8.1) и записать каноническое уравнение прямой, проходящей через точку
в которой пересекается вторая прямая с плоскостью (8.17). (Способ нахождения этой точки рассмотрен в задаче 8.1) и записать каноническое уравнение прямой, проходящей через точку 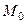 с направляющим вектором
с направляющим вектором 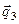 .
.
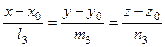 (8.19)
(8.19)
Задача 8.5.
Составить уравнение прямой, проходящей через точку 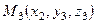 и пересекающейся с каждой из скрещивающихся прямых (8.20) и (8.21)
и пересекающейся с каждой из скрещивающихся прямых (8.20) и (8.21)
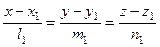 (8.20)
(8.20)
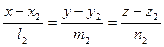 (8.21)
(8.21)
Решение.
Через точку 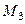 и каждую из прямых можно провести плоскость (задача 8.2). Линия пересечения этих плоскостей и есть искомая прямая.
и каждую из прямых можно провести плоскость (задача 8.2). Линия пересечения этих плоскостей и есть искомая прямая.
Задачи № 1039, 1044, 1050, 1052, 1066, 1071, 1072, 1078, 1083.
Дата публикования: 2015-07-22; Прочитано: 1137 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
