Примеры NP-полных задач

Для того чтобы доказать NP -полноту задачи, необходимо, согласно определению, доказать, во-первых, принадлежность задачи классу NP, а во-вторых, доказать возможность построения алгоритма сведения любой задачи класса NP к данной. Очевидно, что это достаточно сложная процедура.

Лемма 3, доказанная выше, дает реальный способ доказательства NP -полноты произвольной задачи L, заключающийся в следующем:

1) доказать, что L Î NP;

2) выбрать некоторую NP -полную задачу L ’ (L ’Î NPC) и свести ее к данной;

3) доказать, что построенный алгоритм сведения полиномиален.

Однако чтобы воспользоваться этим способом, необходимо иметь в арсенале хотя бы одну задачу, NP -полнота которой уже доказана. Роль такой NP -полной задачи принадлежит задаче распознавания из булевской логики, которую обычно называют ВЫПОЛНИМОСТЬ (сокращенно ВЫП).

Задача ВЫПОЛНИМОСТЬ

Пусть Х ={ х ₁, х ₂,…, х_m } − множество булевских пере­менных. На множестве переменных построено множество литералов U ={ u ₁, u ₂,…, u _{2· m} }. Литералом u называется переменная х или ее отрицание .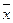

На множестве литералов построена формула j, являющаяся конъюнкцией произвольного числа дизъюнкций, состоящих из произвольного числа литералов.Формула j называется выполнимой в том и только в том случае, если найдется некоторый набор значений переменных на множестве X,на котором формула j принимает истинное значение.Такой набор значений переменных называется выполняющим на­бором для формулы j. В противном случае (если нет выполняющего набора значений переменных) формула называется невыполнимой.

Задача ВЫПОЛНИМОСТЬ формулируется следующим образом.

Дано множество переменных X, на котором построена формула j. Определить, выполнима формула j или нет.

Например, пусть X= { x _1, x ₂}, 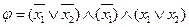. Это индивидуальная задача из ВЫПОЛНИМОСТИ, ответ на которую – «да», так как существует выполняющий набор x ₁= false, x ₂= true. А формула 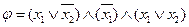– индивидуальная за­дача, ответ на которую – «нет», так как не существует выполняющего набора.

NP -полнота данной задачи была доказана Куком.

Теорема Кука. Задача ВЫПОЛНИМОСТЬ NP -полна.

Для доказательства использовался аппарат машин Тьюринга (см. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи).

Задача 3-ВЫПОЛНИМОСТЬ

Формулировка задачи 3-ВЫПОЛНИМОСТЬ (3-ВЫП): дано множество переменных X, на котором построена формула j, являющаяся конъюнкцией произвольного числа трехлитеральных дизъюнкций. Определить, выполнима формула j или нет.

Например, пусть X ={ x _1, x ₂, x ₃}, 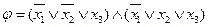. Формула выполнима, так как существует выполняющий набор, например, x ₁= false, x ₂= true, x ₃= false.

Теорема. Задача 3-ВЫП NP -полна (3-ВЫПÎ NPC).

Доказательство

1. Задача 3-ВЫПÎ NP, так как проверяется за полиномиальное время (в качестве сертификата можно рассматривать выполняющий набор). Действительно, для того чтобы проверить, является ли некоторый набор выполняющим для формулы из k дизъюнкций, необходимо выполнить действий О(3· k).

2. Построим алгоритм сведения NP -полной задачи ВЫП к задаче
3-ВЫП, т. е. преобразования произвольной формулы j_вып ÎВЫП к задаче
j_3-вып Î3-ВЫП. Для этого укажем правила преобразования каждой дизъюнкции 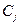формулы j_вып в конъюнкцию трехлитеральных дизъюнкций 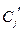формулы j_3-вып так, чтобы выполнялось условие 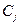– выполнима Û 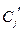– выполнима.

Пусть дизъюнкция 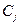имеет вид: .

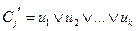1) k =1, .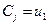

Введем набор дополнительных переменных Y ={ y ₁, y ₂} и построим формулу 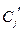следующим образом:

.

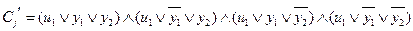Очевидно, что истинность формулы 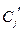зависит лишь от истинности литерала u ₁, следовательно, 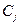– выполнима Û 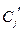– выполнима.

2) k =2, .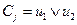

Введем набор дополнительных переменных Y ={ y ₁} и построим формулу 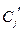следующим образом:

.

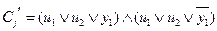Очевидно, что истинность формулы 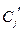зависит лишь от истинности выражения 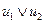, следовательно, 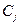– выполнима Û 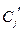– выполнима.

3) k =3, .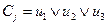

Преобразования дизъюнкции не требуется, т. е. = .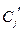

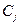4) k ≥4, .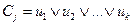

Введем набор дополнительных переменных Y={y₁, y₂, …, y_k-3} и построим формулу 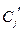следующим образом:

.

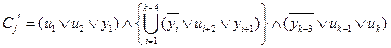Например,

a) пусть 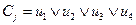, тогда Y={y₁} ;

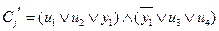b) пусть 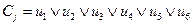, тогда Y={y₁, y₂, y₃} .

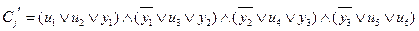Очевидно, что если формула 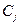невыполнима, то 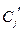также невыполнима, следовательно, 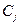– выполнима Û 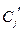– выполнима.

3. Построенный алгоритм является алгоритмом сведения, так как j_вып выполнима Û j_3-вып выполнима. Данный алгоритм полиномиален, время преобразования пропорционально длине формулы j_вып, а число трехлитеральных дизъюнкций в j_3-вып ограниченно полиномом от m·n, где m число дизъюнкций в j_вып, n – число литералов в j_вып.

Таким образом, в силу леммы 3 задача 3-ВЫП NP -полна.

Задание

1) Дана следующая формула:

.

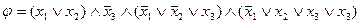Преобразовать ее в формулу задачи 3-ВЫП.

2) Привести пример невыполнимой формулы задачи 3-ВЫП.

Задача о КЛИКЕ

Определение. Кликой в неориентированном графе G =(V, E) называется подмножество вершин V ’Í V, каждые две из которых соединены ребром графа.

Таким образом, клика – это множество вершин полного подграфа графа.

Оптимизационная задача о клике. Определить максимальный размер клики в данном графе.

Задача разрешения (КЛИКА). Даны граф G и число k. Требуется установить, есть ли в графе G клика размера k.

Для решения задачи можно перебрать все подмножества вершин размера k в графе G (их количество равно числу сочетаний – 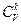) и проверить, есть ли среди них клика (сложность проверки для каждого подмножества 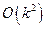). Таким образом, для решения задачи о клике требуется действий 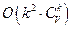, т. е. это задача экспоненциальной сложности (труднорешаемая).

Теорема. Задача о клике NP -полна (КЛИКАÎNPC).

Доказательство.

1. Задача КЛИКАÎ NP, так как проверяется за полиномиальное время (в качестве сертификата можно рассматривать клику размера k). Действительно, для того чтобы проверить, является ли некоторое подмножество из k вершин графа G кликой, необходимо выполнить действий О(k ²).

2. Построим алгоритм сведения NP -полной задачи 3-ВЫП к задаче
КЛИКА, т. е. алгоритм преобразования произвольной формулы j_3-вып Î3-ВЫП в пару (G, k)ÎКЛИКА. Для этого укажем правила преобразования формулы 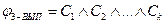в граф G=(V, E), в котором существует клика размера k тогда и только тогда, когда формула j_3-вып выполнима.

Пусть дана формула 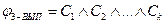, где С_i – дизъюнкция трех литералов. Для построения графа G необходимо, во-первых, задать множество вершин V, а во-вторых, множество ребер Е. Сделаем это следующим образом:

1) для каждой дизъюнкции строим по три вершины – по одной на каждый литерал, таким образом, всего в графе 3· k вершин;

2) построим ребра по следующему правилу: две вершины графа G соединяются ребром тогда и только тогда, когда они соответствуют литералам разных дизъюнкций и соответствующие им литералы совместны (т. е. один не является отрицанием другого).

Например, дана формула 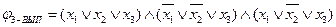, тогда граф G будет иметь вид:

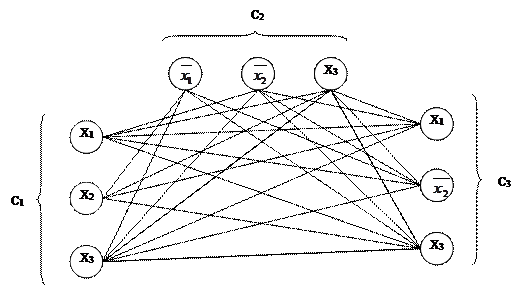
Покажем, что описанное преобразование действительно является сведением, т. е. докажем, что формула j_3-вып выполнима Û в графе G=(V, E) существует клика размера k.

1) Предположим, что формула имеет выполняющий набор, следовательно, в любой дизъюнкции формулы имеется хотя бы один истинный литерал. Выберем по одному истинному литералу из каждой дизъюнкции, так как они попарно совместны, то существуют ребра, их соединяющие, т. е. образуют клику.

Например, для формулы 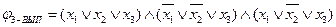существует выполняющий набор (x ₁= true, x ₂= false, x ₃= true). Вершины, соответствующие этим литералам, попарно соединены ребрами, следовательно, образуют клику, которая выделена жирными линиями:

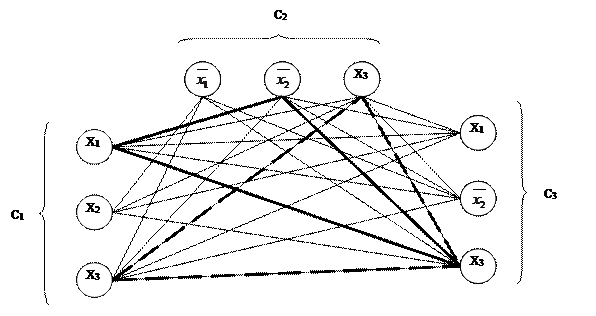
2) Пусть в графе есть клика размера k. В каждой тройке, соответствующей одной дизъюнкции, вершины не соединены друг с другом, следовательно, клика содержит ровно по одной вершине из каждой тройки. Рассмотрим соответствующие им литералы и объявим их истинными. Совместность литералов гарантирует, что их не придется объявлять одновременно истинными и ложными. Если не все переменные получили значения, то им значение придается произвольно, так как от них истинность формулы не зависит.

Например, в графе G есть клика, образованная вершинами (x ₃, x ₃, x ₃) (клика выделена пунктиром). Объявляем литерал x ₃ истинным, т. е. x ₃= true. Действительно, эта переменная, независимо от значений, обращает формулу 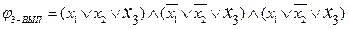в истину, значит, значения для переменных x₁ и x₂ можно указать произвольно.

3) Построенный алгоритм является алгоритмом сведения, так как формула j_3-вып выполнима Û в графе G=(V, E) существует клика размера k. Данный алгоритм полиномиален, так как время сведения ограничено сверху полиномом O((3· k)²).

Таким образом, в силу леммы 3 задача КЛИКА NP -полна.

Задание

1) Построить граф G =(V, E)ÎКЛИКА, соответствующий формуле .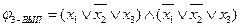

2) Построить граф G =(V, E)ÎКЛИКА, соответствующий формуле .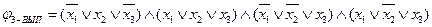

3) Используя решение задачи о КЛИКЕ, найти выполняющий набор для формулы .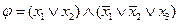

Задача о ВЕРШИННОМ ПОКРЫТИИ

Определение. Множество вершин V ’Í V графа G =(V, E) называется вершинным покрытием графа G, если у любого ребра графа хотя бы один из концов входит в V ’.

Размер вершинного покрытия – количество вершин вершинного покрытия.

Оптимизационная задача о вершинном покрытии. Определить размер минимального вершинного покрытия в данном графе (найти минимальное вершинное покрытие).

Задача разрешения (ВП). Дан граф G и число k. Требуется установить, существует ли в графе G вершинное покрытие размера k.

Для решения задачи можно перебрать все подмножества вершин размера k в графе G (их количество равно числу сочетаний – 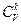) и проверить, у каждого ли ребра графа хотя бы одна из концевых вершин принадлежит выбранному подмножеству (сложность проверки для каждого подмножества 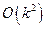). Таким образом, для решения задачи о клике требуется действий 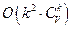, т. е. это задача экспоненциальной сложности (труднорешаемая).

Теорема. Задача о вершинном покрытии NP -полна (ВПÎ NPC).

Доказательство

1. Задача ВПÎ NP, так как проверяется за полиномиальное время (в качестве сертификата можно рассматривать вершинное покрытие размера k). Действительно, для того чтобы проверить, является ли некоторое подмножество из k вершин графа G вершинным покрытием, необходимо выполнить действий О(k ²).

2. Построим алгоритм сведения NP -полной задачи КЛИКА к задаче
ВП, т. е. алгоритм преобразования произвольной пары (G, k)ÎКЛИКА в пару (G ’, k ’)ÎВП. Для этого рассмотрим дополнение графа G.

Дополнением графа G=(V, E) называется граф 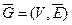, где 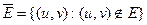– множество ребер полного графа, не вошедших в G.

Например:

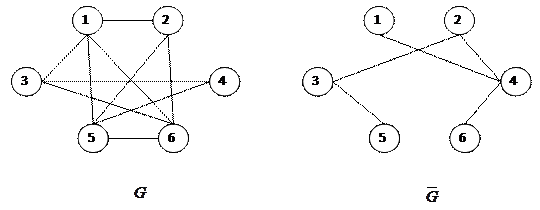
В графе 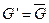существует вершинное покрытие размера k ’=| V |- k Û в графе G существует клика размера k.

Действительно, если в G существует клика размера k, то ее дополнение образует вершинное покрытие графа 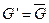, имеющее размер | V |- k: любое ребро графа 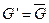отсутствует в графе G, поэтому один из концов этого ребра должен быть вне клики. И наоборот, дополнение к вершинному покрытию графа 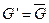является кликой графа G: если какие-то две вершины этого дополнения не связаны ребром в графе 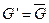, то они связаны ребром в графе G, и это ребро не покрыто.

3. Построенный алгоритм является алгоритмом сведения, так как в графе 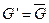существует вершинное покрытие размера k ’=| V |- k Û в графе G существует клика размера k. Данный алгоритм полиномиален, так как. время сведения ограничено сверху полиномом O(| V |²).

Таким образом, в силу леммы 3 задача ВП NP -полна (ВПÎ NPC).