Полиномиальная сводимость и NP-полные задачи

Наиболее убедительным аргументом в пользу того, что классы P и NP различны, является существование так называемых NP -полных задач.
NP -полные языки являются самыми «трудными» в классе NP. При этом трудность языков можно сравнивать, сводя один язык к другому.

Полиномиальная сводимость

Определение. Язык L ₁ за полиномиальное время к языку L ₂
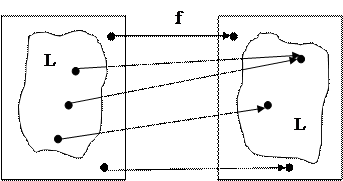
(обозначение: L ₁≤ _pL ₂ или L ₁ 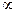L ₂), если существует такая функция
f: {0, 1}^*, вычислимая за полиномиальное время, что для любого слова
х Î{0, 1}^*: x Î L ₁ Û f (x)Î L ₂ (х является индивидуальной задачей L ₁ тогда и только тогда, когда f (x) является индивидуальной задачей L ₂).

Функцию f называют сводящей функцией, а полиномиальный алгоритм A_f, вычисляющий функцию f, – сводящим алгоритмом.

" x Î L ₁ ® f (x)Î L ₂

" x Ï L ₁ ® f (x)Ï L ₂

Лемма 1. Если язык L ₁Í{0, 1}^* сводится за полиномиальное время к языку L ₂Í{0, 1}^* и L ₂ принадлежит классу P, то L ₁ также принадлежит классу Р (если L₁ 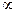L₂ и L₂ÎP, то L₁ÎР).

Доказательство

1) L ₁ 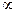L ₂, следовательно, существует полиномиальный сводящий алгоритм А;

2) L ₂Î P, следовательно, существует полиномиальный алгоритм 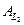распознавания языка L ₂.

Возьмем произвольное слово х Î L ₁ и с помощью алгоритма А сведем его к слову А (х)Î L ₂, а затем определим, принимается или отвергается слово А (х) полиномиальным алгоритмом 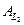. Из определения полиномиальной сводимости следует, что слово А (х) допускается алгоритмом 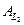тогда и только тогда, когда слово x допускается алгоритмом, распознающим язык L ₁. Таким образом, последовательное выполнение алгоритмов А и 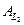дает алгоритм распознавания языка L ₁, и этот алгоритм полиномиален (сумма полиномов есть полином), т. е. L ₁Î P.

Лемма 2. Отношение полиномиальной сводимости транзитивно
(если L₁ 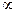L₂ и L₂ 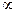L₃, то L₁ 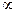L₃).

Определение. Языки L ₁ и L ₂ полиномиально эквивалентны, если сводятся друг к другу.

Понятие полиномиальной сводимости позволяет произвести классификацию языков по степени их «трудности». Запись L ₁ 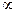L ₂ можно интерпретировать так: сложность языка L ₂ не более чем полиномиально превосходит сложность языка L ₁. Наиболее трудные в этом смысле – NP -полные языки.

Определение. Язык L Í{0, 1}^* называется NP -полным:

1) если L Î NP;

2) L ’ 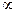L для любого языка L ’Î NP.

Обозначение класса NP -полных языков – NPC.

Лемма 3. Если языки L ₁ и L ₂ принадлежат классу NP, L ₁ – это NP -полный язык и L ₁ полиномиально сводится к L ₂, то L ₂ также NP -полный язык (если L₁ÎNP, L₂ÎNP, L₁ÎNPC и L₁ 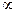L₂, то L₂ÎNPС).

Доказательство. Так как L ₂Î NP, то, согласно определению, достаточно доказать, что любой язык L ’Î NP полиномиально сводится к языку L ₂ (L ’ 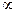L ₂).

По условию леммы L ₁Î NPC, следовательно, любой язык L ’Î NP сводится к языку L ₁ (" L ’Î NP: L ’ 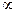L ₁), а язык L ₁ сводится к языку L ₂ (по условию леммы L ₁ 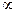L ₂). По свойству транзитивности полиномиальной сводимости (лемма 2) " L ’Î NP: L ’ 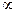L ₁, L ₁ 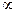L ₂, следовательно, " L ’Î NР: L ’ 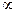L ₂, т.е язык L ₂Î NPC.

Основное свойство NP-полных языков: если некоторый NP -полный язык разрешим за полиномиальное время, то классы P и NP эквивалентны (P=NP), т. е. если в классе NPС существует язык разрешимый за полиномиальное время, то все языки класса NPC разрешимы за полиномиальное время.

Доказательство. Пусть L – NP -полный язык, который одновременно оказался разрешимым за полиномиальное время (L Î NPC и L Î P). По определению NP -полного языка справедливо утверждение: любой язык L ’, проверяемый за полиномиальное время, полиномиально сводится к языку L (" L ’Î NP: L ’ 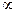L). Таким образом, " L ’Î NP: L ’ 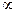L и L Î P, значит, по лемме 1 следует, что " L ’Î NP разрешима за полиномиальное время (" L ’Î NP: L ’Î P), т. е. классы P и NP совпадают.