Ортогональные преобразования плоскости

Определение. Ортогональным преобразованием плоскости P называется линейный оператор Q вида

,

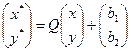матрица которого

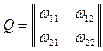
ортогональная в любой ортонормированной системе координат.

Заметим, что ортогональное преобразование является частным случаем аффинного преобразования, поскольку в силу теоремы 11.3 имеет место либо 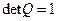, либо 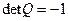. Помимо приведенных в предыдущем параграфе аффинных свойств, ортогональные преобразования обладают своими специфическими особенностями.

Теорема 11.15 Линейный оператор на плоскости является ортогональным, если его матрица ортогональная хотя бы в одной ортонормированной системе координат.

Теорема 11.16 В ортонормированной системе координат ортогональное преобразование плоскости сохраняет:

(1) скалярное произведение векторов;

(2) длины векторов и расстояния между точками плоскости;

(3) углы между прямыми.

Доказательство.

(1). Пусть дано ортогональное преобразование плоскости с матрицей 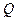в ортонормированной системе координат 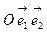. Тогда скалярное произведение векторов 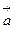и 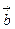с координатными представлениям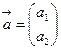и и 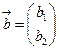выражается в следующем виде

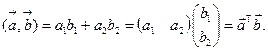
Тогда для скалярного произведения образов векторов 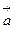и 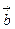, принимая во внимание ортогональность матрицы 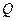, получаем

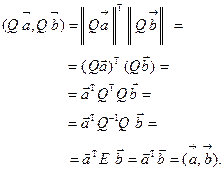
Равенство 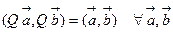и означает, что при ортогональном преобразовании плоскости скалярное преобразование сохраняется в любом ортонормированном базисе.

(2). Из сохранения при ортогональном преобразовании скалярного произведения для любой пары векторов следует сохранение длин векторов, поскольку этом случае

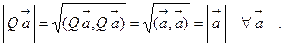
(3). Поскольку в силу (2) при ортогональном преобразовании равные треугольники переходят в равные, то будут сохраняться и величины углов между векторами на плоскости.

Теорема доказана.

Используя свойства ортогональных преобразований, можно показать, что для аффинных преобразований справедлива следующая важная теорема.

Теорема 11.17 Каждое аффинное преобразование может быть представлено в виде произведения ортогонального преобразования и двух сжатий по взаимно ортогональным направлениям.

Доказательство.

Для этого достаточно убедиться, что матрица каждого аффинного преобразования в любом ортонормированном базисе 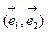может быть представлена в виде произведения ортогональной матрицы и диагональной матрицы с положительными значениями диагональных элементов.

По теореме 11.4 существует ортогональный (но не обязательно нормированный) базис 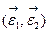, в который данное аффинное преобразование 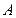переведет исходный ортонормированный базис 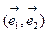. При этом существуют положительные нормирующие множител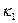и и 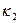, такие, что

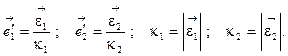
То есть, 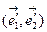– ортонормированный базис.

С другой стороны, линейное преобразование 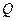, переводящее ортонормированный базис 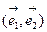в ортонормированный базис 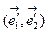, очевидно, ортогональное и имеет в исходном базисе ортогональную матрицу 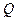. Тогда будут справедливы соотношения

; ; ,

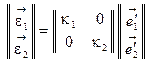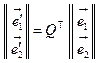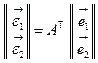из которых следует равенство

.

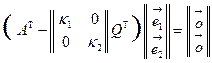Тогда в силу линейной независимости базисных векторов 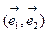мы имеем

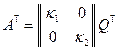
или, после транспонирования обеих частей этого равенства,

.

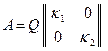Таким образом, аффинное преобразование представимо в виде произведения ортогонального преобразования и оператора "сжатия к осям"

Теорема доказана.