Линейные операторы на плоскости

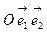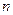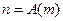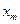Пусть на плоскости с декартовой системой координат каждой ее точке m поставлена в однозначное соответствие точка , то есть, согласно определению, задано преобразование этой плоскости . Пусть координатные представления радиусов-векторов этих точек суть и , тогда координаты и 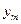будут некоторыми функциями от 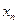и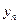

,

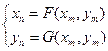и потому равенство

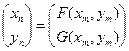
можно рассматривать как представление оператора 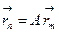в системе координат .

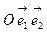Далее мы будем рассматривать частные, но важные для приложений виды функци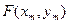й и .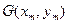

Определение. Оператор 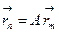называется линейным оператором, если в каждой декартовой системе координат 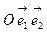он задается формулами

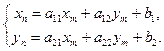
При помощи операций с матрицами линейный оператор может быть записан в виде

,

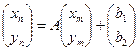где матрица

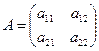
называется матрицей линейного оператора 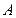(координатным представлением 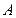) в декартовой системе координат .

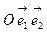Определение. Оператор 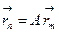называется линейным однородным оператором, если он удовлетворяет предыдущему определению и .

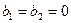Если 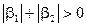оператор 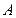называется неоднородным.

Пример 5. Линейным однородным оператором является оператор 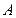, действие которого сводится к умножению координат радиуса-вектора прообраза на фиксированные положительные числа, называемый «оператором сжатия ( или “ растяжения ” ) по осям», имеющий матрицу

,

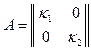где числа 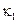и 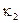– коэффициенты сжатия (или растяжения);

Пример 6. О ператор ортогонального проектирования радиусов-векторов точек плоскости на некоторую заданную ось, проходящую через начало координат, также является линейным однородным оператором.

Теорема 11.5 Для линейного однородного оператора 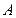справедливы соотношения:

,

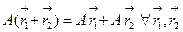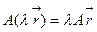
В справедливости утверждения теоремы можно убедиться непосредственной проверкой, используя правила действия с матрицами.

Теорема 11.6 Если для некоторого оператора 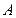справедливы соотношения

,

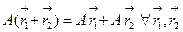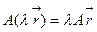
то этот оператор линейный и однородный.

Доказательство.

Пусть 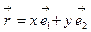и 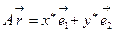– соответственно координатные разложения для прообраза и образа, тогда

.

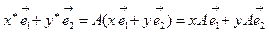Вводя обозначения

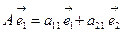и ,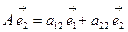

получаем

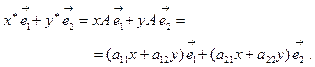
А в силу линейной независимости векторов 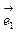и

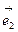
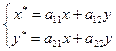, или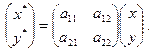

Теорема доказана.

Заметим, что для вектора 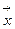, имеющего координатное представление 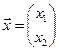,в базисе 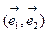, при любом линейном преобразовании образом 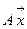является вектор с координатным представлением

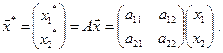
Из теорем 11.5 и 11.6 вытекают важные следствия.

Следствие 1. Столбцами матрицы линейного однородного оператора 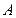в базисе 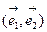являются координатные представления векторов 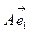и .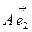

Следствие 2. Каждому линейному однородному оператору преобразования плоскости в конкретном базисе соответствует однозначно определяемая квадратная матрица второго порядка, а каждая квадратная матрица второго порядка задает в этом базисе некоторый линейный однородный оператор.

Выясним теперь, как изменится матрица линейного однородного оператора при замене базиса. Имеет место

Теорема 11.7 Пусть в системе координат 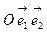некоторый однородный линейный оператор имеет матрицу A. Тогда в системе координат 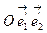этот оператор будет иметь матрицу 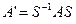, где S – матрица перехода от 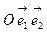к .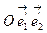

Доказательство.

Пусть в исходной системе координат действие линейного оператора 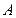задается формулой 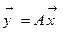, а в новой системе координат – 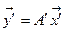, и пусть S – матрица перехода от 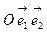к 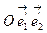с формулами перехода

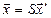и .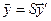

Подставляя два последних соотношения в первое и принимая во внимание утверждение о невырожденности матрицы перехода S (то есть существование матрицы 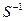), получаем, что

.

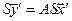или

Откуда и следует, что

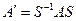
Теорема доказана.