Розвязув систем матричним способом

Якщо

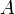— основна матриця системи,

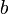— вектор-стовпчик вільних членів,

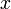— вектор-стовпчик невідомих;

то має місце рівність:

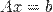
Якщо матриця 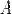є квадратною та невиродженою, то для неї існує обернена матриця. Помноживши обидві частини рівняння зліва на 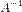, отримаємо

.

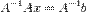оскільки A ^{− 1} A = I та Ix = x, то отримаємо формулу:

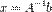
7 Ранг матриці способи обчислення

Ранг матриці — порядок найбільших відмінних від нуля мінорів цієї матриці

Ранг матриці не міняється при елементарних перетвореннях матриці (перестановці рядків або стовпців, множенні рядка або стовпця на відмінне від нуля число і при складанні рядків або стовпців).

Ранг матриці розмірності 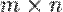називають повним, якщо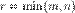

сновними методами обчислення рангу матриці є методи оточення мінорів (теоретичний) і метод елементарних перетворень (практичний).

Метод оточення мінорів полягає в тому, що в ненульовій матриці шукається довільний базисний мінор.

Метод елементарних перетворень полягає в тому, що за допомогою елементарних перетворень знаходиться деяка максимальна лінійно незалежна система рядків матриці. Можливо із зведенням матриці до трикутного вигляду (метод Гауса).

Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого по­рядку дорівнюють нулю, то r = 1. У випадку, коли є мінор другого по­рядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори по­рядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k –1

Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Простіший метод грунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме:

а) переставити місцями два рядки (стовпці);

б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

в) додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число.

8 Теорема Кронекера - Капеллі — критерій сумісності системи лінійних алгебраїчних рівнянь:

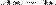
СЛАР має розв'язки тоді і тільки тоді,коли ранг її матриці 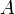дорівнює рангу її розширеної матриці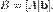

Причому система має єдине рішення, якщо ранг дорівнює числу невідомих і нескінченно багато рішень, якщо ранг менше числа невідомих

9. Вектор.Лінійні операції з векторами.

Вектор – впорядкована пара точок(М,N),перша з яких називається початком векторав,друга-його кінцем. Вектор з початком М та кінцем N позн.MN(з рисочкою) і зображається відрізком,на якому стрілкою позначається напрям від М до N. Якщо ж неістотно,які саме початок і кінець вектора,його позначають однією буквою,наприклад, а і б (з рискою) тощо. відстань між М та N називається довжиною або модулем вектора.

Дії з векторами виконуються за правилами:

1. Додавання: 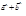= (а_х + b_х, а_у + b_у, а_z + b_z).

2. Множення вектора на число   R: .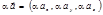

10. Скалярний добуток векторів та його властивості.

Скалярним добутком двох векторів і наз добуток довжин цих векторів на косинус кута, утвореного векторами. Якщо хоча б один із векторів = нулю, то кут між векторами не визначений і за означенням скалярний добуток = нулю.

Скалярний добуток двох векторів = добутку довжини одного з них на проекцію іншого на напрям першого.

1. .

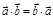2. .

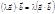3. .

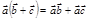4. .

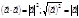5. 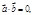якщо 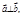і навпаки, 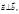якщо .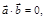

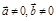11. Пряма на площині.

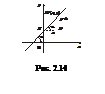
Нехай задано деяку пряму знайдемо її рівняння.

Точка М (х, у) лежить на

прямій тоді і тільки тоді, коли виконується умова 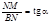.Позначимо tg a = k і назвемо цю величину кутовим коефіцієнтом прямої лінії. Тоді, враховуючи, що NM = y – b, BN = x, маємо рівняння прямої з кутовим коефіцієнтом у = kx + b. (2.14)

Нехай деяка точка М ₁ (х ₁, у ₁) належить заданій прямій, тоді у ₁ = kx ₁ + b. Знайдемо з цього рівняння значення b і, підставивши його в рівняння прямої дістанемо: у – у ₁ = k (х – х ₁) (2.15)

— рівняння прямої, що проходить через задану точку М ₁ (х ₁, у ₁).

Нехай ще одна точка М ₂ (х ₂, у ₂) також належить заданій прямій, тоді з означення лінії маємо: у ₂ – у ₁ = k (x ₂ – x ₁).

Знайдемо значення k з останнього співвідношення і, підставивши його в рівнянняпрямої, дістанемо: 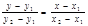. (2.16)

Останнє рівняння (2.16) називається рівнянням прямої, що проходить через дві задані точки.

12. Відстань від точки до прямої

Нехай задано деяку точку М ₀ (х ₀, у ₀) і пряму l: Ах + Ву + С = 0. Пересвідчимось, що М ₀ не лежить на прямій, Ах ₀ + Ву ₀ + С ¹ 0, тоді відстань від точки М ₀ (х ₀, у ₀) до прямої Ах + Ву + С = 0 можна знайти за формулою: .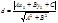

13. Еліпс,гіпербола,парабола.

Еліпс.. геометр місце точок, сума відстані яких до 2-х фіксованих точок(фокусів) і величина стала

Тоді 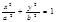канонічне рівняння еліпса, де b ² = а ² – с ².

Гіпербола. геометр місце точок, різниця відстані яких до 2-х фіксованих точок(фокусів) і величина стала

точки F ₁ (– c, 0) і F ₂ (c, 0) — фокуси гіперболи, точка М (х, у) — точка визначеної множини. Тоді .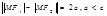

Канонічне рівняння гіперболи має вигляд: 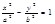, де b ² = c ² – a ²

. Парабола.. геометр місце точок, рівновіддалених від д точки (фокуса) і д. прямої(директриси)

За означенням r = d, отже 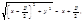або у ² = 2 рх — канонічне рівняння параболи, коли e = 1.

14. Площина. Пряма у просторі.

Нехай задано прямокутну систему координат Охуz, площину a, вектор 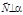, який має координати 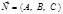, і точку 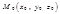, яка належить площині

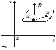
Точка М (х, у, z) — довільна точка площини. Ця точка належить площині лише в тому разі, коли вектори 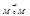і 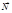взаємно перпендикулярні.Умова перпендикулярності векторів

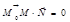. (2.25)

Останній вираз можна розглядати як векторне рівняння площини. Координати вектора 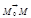дорівнюють відповідно х – х ₀,
у – у ₀, z – z ₀. Записавши вираз (2.25) у розгорнутому вигляді, дістанемо рівняння площини, що проходить через задану точку:

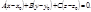(2.26)

Розкривши дужки в і позначивши 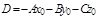, дістанемо загальне рівняння площини:

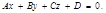
Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:

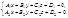(2.31)

Зрозуміло, що ці площини мають бути непаралельними, тобто їхні нормальні вектори 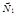, 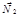— не колінеарні. Система (2.31) називається загальним рівнянням прямої. Дістанемо ще деякі форми рівняння прямої.

Канонічне рівняння прямої. Нехай у системі координат Охуz задано пряму l і ненульовий вектор 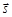, колінеарний цій прямій. Точка 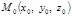належить прямій, а напрямний вектор 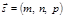. Тоді довільна точка М (х, у, z) лежатиме на прямій тоді і тільки тоді, коли вектори 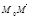і 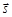колінеарні:

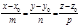. (2.32)

Рівняння називається канонічним рівнянням прямої у просторі.

Рівняння прямої, що проходить через дві задані точки.

Нехай дві точки 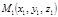і 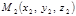належать прямій у просторі. Тоді вектор 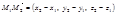можна розглядати як напрямний вектор прямої. Замінюючи ним вектор 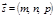у рівнянні (2.32), дістанемо шукане рівняння прямої у просторі

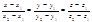
15. Поверхні другого порядку.

Поверх ні в просторі назив поверхнями 2-го пор якщо їх рівняння містять хоч би одну з координат х, у, зет у другому степені

Поверхня другого порядку як геометричний об’єкт не змінюється, якщо він заданої прямокутної системи координат перейти до іншої. При цьому рівняння і рівняння, знайдене після перетворення координат, будуть еквівалентні.

Можна довести, що існує система координат, в якій рівняння має найпростіший (або канонічний вигляд.

До поверхонь другого порядку належать, зокрема, циліндричні та конічні поверхні, поверхні обертання, сфера, еліпсоїд, одно порожнинний та двопорожнинний гіперболоїди, еліптичний та гіперболічний параболоїди.

16. Границя функції,границя послідовності

Постійна величина а назив границею зміної вел х якщо абсолютна вел різниці х-а є вел нескінчено малою, тобто модуль х-а менше Е(есетра)

А є границею 2-х зміних якщо для будь-якого як завгодно малого наперед заданого додатного числа Е існує такий r опір точки М(нульове) що тільки т. М(х,у) потрапить у цей пір то матиме місце рівність модульФ(х, у) – А менше Е.

Число а є границею послідовності х, х1, х2…Х(н) якщо для будь-якого наперед заданого числа скільки завгодно малого Ебільше нуля існую такий номер Н, що для всіх нбільшеН викон рівність модуль х(н) – а менше Е

А назив границею у=Ф(х) при х прямує до х(нульового), якщо для будь-якого наперед заданого числа скільки завгодно малого Еменше нуля, знайдеться таке число б більше нуля,що для усіх х відмінних від х(нульового) і які задовольн нерівн модуль х – х(нульове) менше б, викон непів модуль Ф(х) – А менше Е.

А назив грени Ф(Х) при х прямує до а, якщо для будь-якого як завгодно малого додатного числа Е існую б(Е), таке що із нерівн модуль х – а менше б слідує модуль Ф(х) – А менше Е.