A) Вероятность достижения установленной цели за n попыток

Сначала рассмотрим подбрасывание монеты. Мы начнем с изложения связанных с нашей задачей особенностей стандартного Броуновского движения. Howard Tucker обратил на них мое внимание еще в 1974 году, и это, вероятно, наиболее полезный отдельный факт из всех, что я знаю, имея дело с разнообразными проблемами азартных игр и с теорией производных финансовых инструментов. Для стандартного Броуновского движения X (t) мы имеем

где α = а√Т, а β = b/√T. См. Рисунок 2 и Приложение 2, где дан вывод формулы (3.1)

В нашем случае а < 0, b > 0, так что lim_T→∞ P(X(t) ≥ at + b, 0 ≤ t ≤ T)=1.

Пусть f будет долей ставки. Пусть Y_i, i=1..., n,– независимые тождественно распределенные (i.d.d..) величины. P (Y_i=1)=p > 1/2, P (Y_i =-1)=q < 1/2; пусть также p < 1, во избежание тривиального случая p= 1.

Ставим фиксированную долю ставки f, 0 < f < 1, в каждой попытке. Пусть V_k будет величина капитала игрока или инвестора через k попыток, при начальном значении V₀. Выберем Vo= 1 (без потери общности); число попыток n; цель С > 1.

Какова вероятность того, что V_k ≥ С для некоторого k, 1 ≤ k ≤ n? Она та же самая, как вероятность, что log V_k; ≥ log C для некоторого k, 1 ≤ k ≤ n. Обозначая ln=log_e, имеем:

Сдвиг за n попыток: nm

тогда и только тогда, когда:

Дисперсия за n попыток: s²n

где

, или, равносильно:

Мы хотим найти вероятность Рrob(S_k ≥ ln C - mk, 1 ≤ k ≤ n).

Для этого мы используем нашу формулу Броуновского движения, чтобы аппроксимировать S_n через Prob (X(t) ≥ lnС - Хt/s², 1 ≤ t ≤ s²n) где каждое значение S_n приближено равно X(t) со сдвигом 0 и дисперсией s² (0 ≤ t ≤ s², s² ≤ t ≤ 2s²..., (n - 1)s² ≤ t ≤ ns²). Замечание: приближение "хорошо" только для "больших" n.

Тогда в формуле (3.1):

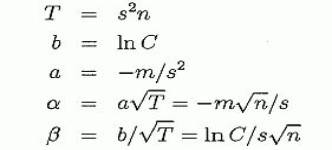
Пример 3.1

Откуда P(·)=0.9142

Пример 3.2

Повторим решение Примера 3.1 при

f =0.02;

тогда m =0.000200013

s² =0.000399947,

и P(∙) =0.9214