Краткие теоретические положения

Как правило, задачи производственного менеджмента сводятся к задачам, в которых требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности. Одним из методов решения таких задач является графический метод. Он основан на известных положениях о том, что линейное уравнение описывает множество точек, лежащих на одной прямой, а линейное неравенство - некоторую область на плоскости.

Рассмотрим задачу производственного планирования.

Пусть известен перечень продуктов, которые предприятие может производить без дополнительных капитальных вложений. Вместе с тем известны вид и количество ресурсов, отпущенных для производства, и структура материальных затрат и доходов. Перед предприятием стоит задача выбора плана производства, обеспечивающего получение максимальной прибыли.

Пусть предприятие может производить n различных продуктов. Количество j -го продукта, выпускаемого по плану, обозначим через X_j, тогда план производства имеет вид:

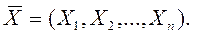
Пусть для организации производства необходимо m видов ресурсов. Количество i -го ресурса - b_i. Потребность i -го ресурса для изготовления единицы j -го продукта - a_ij, а прибыль от производства единицы продукции j -вида - С_{j .} Цель менеджера – максимизировать целевую функцию F(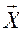), выбрав соответствующий 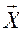из заданного множества значений переменных.

Математическая формулировка задачи в данном случае имеет вид:

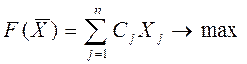
при системе ограничений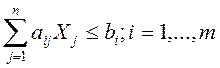

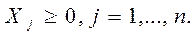
На практике многие экономические параметры (цены на продукцию и сырье, запасы сырья, спрос на рынке, заработная плата и т.д.) с течением времени меняют свои значения. Поэтому оптимальное решение задачи линейного программирования, полученное для конкретной экономической ситуации, после ее изменения может оказаться непригодным или неоптимальным. В связи с этим возникает задача анализа чувствительности задачи, а именно того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение.

Ограничения линейной модели классифицируются следующим образом (рис. 1). Связывающие ограничения проходят через оптимальную точку С, например (1) и (2). Несвязывающие ограничения не проходят через оптимальную точку, например (3), (4) и (5).

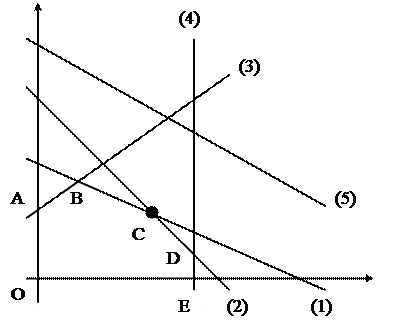
Р и с. 1

Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением, – недефицитным. Область допустимых решений представлена многоугольником ОАВСDЕ.

Ограничение называют избыточным в том случае, если его исключение не влияет на область допустимых решений и, следовательно, на оптимальное решение, например, (5). Выделяют следующие три задачи анализа на чувствительность.

1. Анализ сокращения или увеличения ресурсов:

1) на сколько можно увеличить (ограничения типа ≤) или уменьшить (ограничения типа ≥) запас дефицитного ресурса для улучшения оптимального значения целевой функции?

2) на сколько можно уменьшить (ограничения типа ≤) или увеличить (ограничения типа ≥) запас недефицитного ресурса при сохранении полученного оптимального значения целевой функции?

2. Увеличение (уменьшение) запаса какого из ресурсов наиболее выгодно?

3. Анализ изменения целевых коэффициентов:каков диапазон изменения коэффициентов целевой функции, при котором не меняется оптимальное решение?

Пример 1

Предприятие производит два вида продукции А₁ и А₂ используя сырьё трёх видов: S₁, S₂, S₃. Нормы расхода сырья каждого вида, прибыль на единицу продукции, а также запасы приведены в табл. 1.

Таблица 1

Вид сырья	Нормы расхода сырья на единицу продукции	Наличие сырья
А1	А2
S1
S2
S3
Прибыль от реализации единицы продукции

Математическая модель данной задачи примет вид:

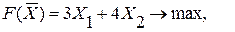
при ограничениях:

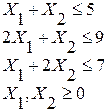
(1) (2) (3) (4)

где Х₁, Х₂ – количество единиц продукции вида А₁ и А₂.

Число переменных равно двум, поэтому для решения задачи можно воспользоваться графическим методом. Изобразим условия производственной задачи на координатной плоскости.

Определяем область допустимых решений из неравенства (1) 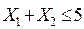. Это область ALM (рис. 2 ).

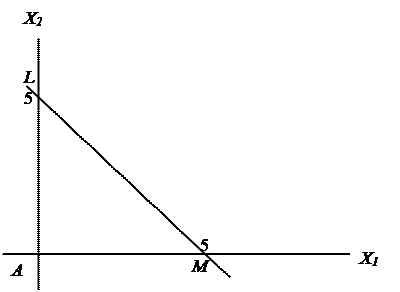
Р и с. 2

Прямая LM пересекает ось Х₂ в точке L (0;5). Это означает, что если все сырье S₁ будет пущено на изготовление продукта А₂, то будет изготовлено 5 единиц данного продукта. Та же прямая пересекает ось Х₁ в точке M (5;0), то есть, если всё сырьё S₁ пустить на изготовление продукта А₁, то будет изготовлено также 5 единиц данного продукта. Для всех точек внутри треугольника ALM выполняется неравенство (1), что означает, что часть сырья будет оставаться.

Аналогичным образом можно изобразить ограничения по сырью S₂ и S₃. Для неравенства (2) 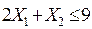область допустимых значений – AGE (рис. 3).

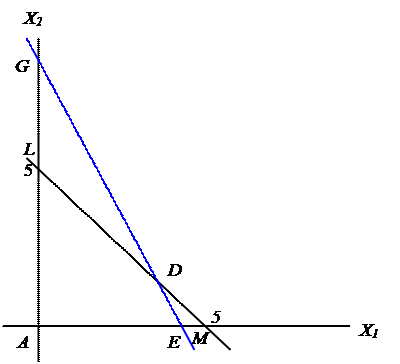
Р и с. 3

Для двух неравенств область допустимых решений - ALDE.

Из третьего неравенства 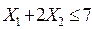область допустимых значений – ABF (рис. 4).

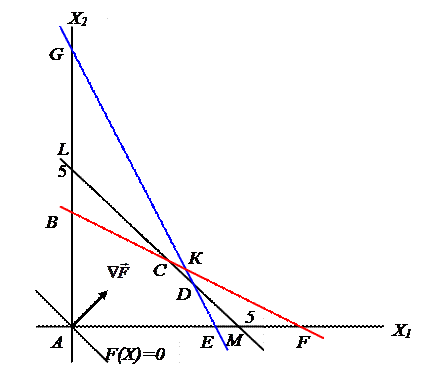
Р и с. 4

Из трех неравенств и с учетом того, что 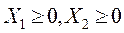область допустимых значений составляет ABCDE.

Затем на этой области наносим целевую функцию – это прямая с нормальным вектором 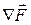(рис. 4). Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. Перемещая прямую F(X) = 0 по направлению векторадо тех пор, пока она не сместится в область недопустимых решений, получим значение целевой функции в точках A, B, C, D, E:

A: F(0;0) = 0;

B: F(0;3,5) = 14;

C: F(3;2) = 17;

D: F(4;1) = 16

E: F(4,5;0) = 13,5.

Отсюда видно, что оптимальное решение находится в точке С:

изготавливается 3 единицы продукции А₁, и 2 единицы продукции А₂, прибыль от реализации составит 17 условных единиц.

Проведем анализ чувствительности к изменениям исходной модели. Например, как повлияет на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции.

1. На сколько можно увеличить запас некоторого вида сырья для улучшения полученного оптимального значения целевой функции?

2. На сколько можно снизить запас сырья при сохранении полученного оптимального значения целевой функции?

3. Увеличение какого вида сырья наиболее выгодно?

4. Каков диапазон изменений того или иного коэффициента целевой функции, при котором не произойдет изменения оптимального решения?

Так как точка С является оптимальной, то ограничения (1) и (3) являются активными, поэтому сырьё S₁ и S₃ является дефицитным, так как расходуется полностью.

Рассмотрим сырьё S₁. При его увеличении прямая LM перемещается параллельно вправо и оптимальная область будет в виде ABKM, то есть оптимальная точка С переходит в точку К (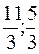). Дальнейшее увеличение запаса сырья S₁ нецелесообразно, так как оно становится неактивным, при этом ограничение сырья S₁ получим, подставляя координаты точки К в (1):

,

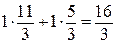а значение целевой функции равно .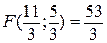

Аналогично рассматривается вопрос о целесообразности увеличения сырья S₃. При этом оптимальная точка С перемещается в точку L (0;5). Запас сырья при этом:

1^.0+2^.5=10,

а значение целевой функции равно F (0;5)=20.

Рассмотрим уменьшение недефицитного сырья S₂. В этом случае прямую KE можно перемещать параллельно себе влево до точки С. Запас сырья S₂ при этом можно уменьшить до величины

2^.3 +1^.2 =8.

Это никак не влияет на оптимальное решение.

Результаты проведенного анализа представлены в табл. 2

Таблица 2

Сырье	Тип сырья	Максимальное изменение запаса	Максимальное изменение прибыли
S1	Дефицитное	16/3 – 5=1/3	53/3 – 51/3 = 2/3
S2	Недефицитное	9 – 8 =1	17 – 17 = 0
S3	Дефицитное	10 – 7 = 3	20 – 17 = 3

Введем ценность дополнительного сырья Y_i:

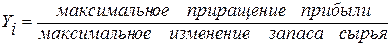
i = 1,…, 3.

Тогда Y₁ =2, Y₂ = 0, Y₃ = 1.

Таким образом, наиболее ценным является сырье S₁, поэтому дополнительные вложения необходимо направлять в первую очередь на закупку этого сырья.

Определим диапазон изменений коэффициентов целевой функции С_j. Графический анализ изменения целевых коэффициентов (например, запасов сырья), не приводящих к изменению оптимального решения, проводится путем вращения линии целевой функции. При небольшом изменении коэффициентов целевой функции прямая F(X) = 17 вращается вокруг точки С. Точка С будет оставаться оптимальной то тех пор, пока прямая F(X) не выйдет за пределы, определяемые первым и третьим ограничениями. Пусть коэффициент С₂ фиксированный (С₂ = 4). Определим диапазон изменения коэффициента С₁. Тангенсы углов наклона:

,

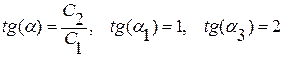где tg (α₁) – угол наклона нормали к прямой (1),

tg (α₃) – угол наклона нормали к прямой (3).

Следовательно, диапазон изменения коэффициента С₁ в целевой функции определится из соотношения: 1≤ 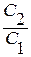≤ 2; то есть 2≤ С₁ ≤4.

Аналогично определяется изменение коэффициента С₂ при фиксированном С₁ = 3:

3≤ С₂ ≤6.

Пример 2

Компания производит два типа деталей для автомобилей X₁ и X₂. Для производства одной детали типа X₁ требуется 1 человеко-час, а для производства одной детали типа X₂ - 2 человеко-часа. Компания располагает фондом рабочего времени 4000 человеко-часов в неделю. Производственные мощности позволяют выпускать максимум 2250 деталей типа X₁ и 1750 деталей типа X₂ в неделю. Каждая деталь типа X₁ требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа X₂ необходимо 5 кг металлических стержней и 2 кг листового железа. Запас каждого вида металла составляет 10000 кг в неделю. Кроме того, еженедельно завод поставляет 600 деталей типа X₁ своему постоянному заказчику. Сколько деталей каждого типа следует производить, чтобы максимизировать общую прибыль за неделю, если прибыль от производства одной детали типа X₁ составляет 30 усл. ед., а от производства детали типа Х₂ - 40 усл. ед.?

Решение:

Сформулируем задачу линейного программирования.

1) Введем переменные

X₁ - количество деталей типа X₁, которые нужно выпустить за неделю;

X₂ - количество деталей типа X₂, которые нужно выпустить за неделю.

2) Целевая функция - прибыль, получаемая за неделю

F(X) = 30X₁ +40X₂ → max,

3) Ограничения на производственный процесс.

Требуемый фонд рабочего времени

1 X₁ + 2 X₂ ≤ 4000; (5)

Требуемая производственная мощность

X₁ ≤ 2250, (6)

X₂ ≤ 1750 (7)

Требуемое количество металлических стержней

2X₁ + 5X₂ ≤ 10000; (8)

Требуемое количество листового металла

5X₁ + 2X₂ ≤ 10000; (9)

Постоянные заказы

X₁ ≥ 600 (10)

Условие неотрицательности

Х₁, Х₂ ≥ 0. (11)

Объединим все ограничения на рис. 5.

В соответствии с рис. 5 максимальную прибыль можно получить при пересечении целевой функцией точки А, т.е. оптимальным будет выпуск 1500 деталей типа X₁ и 1250 деталей типа X₂. При этом прибыль равна

F (150;1250)= 30× 150 + 40× 1250 = 95000 усл. ед.

Очевидно, что при таком решении не все ресурсы используются полностью. Поэтому целесообразно более тщательно проанализировать возможности полного использования ресурсов и предусмотреть меры для их наилучшего применения. Это позволяет выполнить, так называемый, анализ чувствительности.

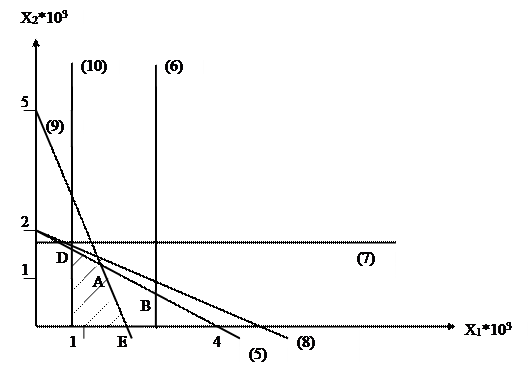
Р и с. 5

В соответствии с рис. 5 два ресурса - фонд рабочего времени и листовой металл - расходуются полностью. Эти ограничения называются лимитирующими. Однако для обоих типов деталей остается неиспользованной часть производственных мощностей и металлические стержни.

Представим систему ограничений примера 2 в виде уравнений. Для этого в каждое ограничение введём дополнительную переменную Si. Принимая неотрицательность Si, т.е. Si ≥ 0, Si прибавляются к левым частям всех ограничений вида «≤» (остаточная переменная) и вычитаются из левых частей при знаке «≥» (избыточная переменная).

Система уравнений имеет вид:

1 X₁ + 2 X₂ + S₁ = 4000

X₁ + S₂ = 2250

X₂ + S₃ = 1750

2 X₁ + 5 X₂ + S₄ = 10000

5 X₁ + 2 X₂ + S₅ = 10000

X₁ - S₆ = 600

При найденных значениях X₁ = 1500, X₂ = 1250, S ₁ = 0 и S₅ = 0 - это лимитирующие ограничения.

Значения остаточных переменных следующие:

S₂ = 750, S₃ = 500, S₄ = 750

Избыточная переменная:

S₆ = 900

Воздействие дополнительного количества лимитирующего фактора. Поскольку один или несколько ресурсов используются полностью, значение целевой функции ограничено. Если появляется дополнительное количество лимитирующего ресурса, то оптимальное решение может быть улучшено. Однако необходимо принять во внимание, что изменение оптимального решения приведет к улучшению значения целевой функции только в том случае, еслисумма дополнительных издержек по обеспечению дополнительным количеством ресурса не превышает сумму прибыли, полученной в результате его использования. С увеличением объема лимитирующего ресурса соответствующееограничение становится менее жестким. Так как жесткость лимитирующего ограничения постепенно снижается, его график будет перемещаться параллельносвоему начальному положению, одновременно будет происходить перемещениеоптимальной крайней точки в направлении, которое улучшает значение целевой функции. Этот процесс будет продолжаться до тех пор, пока какой-либодругой ресурс не будет полностью использован и рассматриваемое ограничениеперестанет быть лимитирующим. Величина, на которую увеличивается значение целевой функции при снижении жесткости лимитирующего ограничения наединицу, т.е. при увеличении количества лимитирующего ресурса на единицу,называется теневой ценой ресурса. Теневая цена ресурса - это стоимость единицы данного ресурса в оптимальном решении. Увеличение объема лимитирующего ресурса на единицу целесообразно только в том случае, если существует возможность его получения по стоимости, которая ниже, чем теневая ценаданного ресурса. Из примера 2 следует, что лимитирующими являются ограничения на фонд рабочего времени и на листовой металл. Рассмотрим сначала последнее из указанных ограничений. Обратимся к графику, изображенному нарис.5. Жесткость ограничения на листовой металл снижается по мере перемещения линии ограничения параллельно ее исходному положению в противоположном направлении от начала координат. Допустимое множество расширяется, а оптимальная крайняя точка перемещается вниз по линии ограничения нафонд рабочего времени, что увеличивает X₁ и уменьшает X₂. Снижение жесткости ограничения на листовой металл является эффективным до тех пор, покалиния ограничения не достигнет точки пересечения ограничений на фонд рабочего времени и производственные мощности для деталей типа X₁, т.е. точки B.

Если и далее снижать жесткость ограничения на листовой металл, оно перестает быть лимитирующим, что приведет к появлению остатка в виде неиспользованного листового металла.

Новой оптимальной крайней точкой является теперь точка B. Координаты точки B можно определить, решив систему уравнений для ограничений на фонд рабочего времени и производственные мощности для детали X₁.

Фонд рабочего времени: X₁ + 2 X₂ = 400 чел.-ч в неделю;

производственные мощности для X₁: X₁ = 2250 деталей в неделю.

Так как X₁ =2250, то, подставив его в уравнение (5), найдем значение X₂:

2250 + 2 X₂ = 4000;

следовательно, X₂ = 875 деталей.

Новым оптимальным ассортиментным набором является производство 2250 деталей типа X₁ и 875 деталей типа X₂ в неделю. Этот ассортиментный набор дает максимальный доход, равный F (2250;875) = 30×2250 + 40 × 875 = 102500 усл.ед. в неделю, таким образом, увеличение дохода составит: 102500 - 9500 = 7500 усл.ед. в неделю. Количество листового металла, используемое для производства данного ассортиментного набора, равно:

5× 2250 + 2× 875 = 13000 кг.

Оно превышает начальное количество на 3000 кг в неделю. В новой оптимальной точке фонд рабочего времени и производственные мощности для деталей X₁ используются максимально.

Дополнительное количество листового металла - 3000 кг - позволяет получать дополнительный доход, равный 7500 усл.ед. в неделю, следовательно, теневая цена данного ресурса составит: 7500: 3000 = 2,50 усл.ед. за кг. Каждый дополнительный килограмм листового металла ведет к увеличению еженедельного дохода 2,50 усл.ед. Из этого следует, что сверхнормативный запас этого ресурса целесообразен только в случае, если стоимость получения любого дополнительного количества ресурса не превышает 2,50 усл.ед. за 1 кг ресурса.

Предположив, что ограничение на листовой металл остается неизменным, применим аналогичную процедуру ко второму лимитирующему ограничению.

Если жесткость ограничения на фонд рабочего времени снизилась на 1 единицу, т.е. появилась возможность использовать 1 чел.-ч рабочего времени дополнительно, то тогда данное ограничение (5) принимает вид:

X₁ + 2 X₂ ≤ 4001.

Данное ограничение параллельно первоначальному, но его линия находится дальше от начала координат по сравнению с исходной линией. Из приведенного выше графика легко видеть, что точка пересечения ограничения на листовой металл и нового ограничения на фонд рабочего времени все еще является оптимальной крайней точкой. В данном случае оптимальным решением является точка с координатами X₁ = 1499,75 и X₂ = 1250,625, что приводит и к значению целевой функции Fmax = 95017,50 усл.ед. Таким образом, значение целевой функции увеличилось на 17,50 усл.ед. Теневая цена фонда рабочего времени составляет 17,50 усл.ед. за 1 чел.-ч. Если можно получить один дополнительный час рабочего времени за дополнительные 17,50 усл.ед. или менее, то это необходимо использовать. Если же стоимость 1 чел.-ч превышает 17,50 усл.ед., то дополнительное количество рабочего времени использовать нецелесообразно.

Какое количество дополнительного рабочего времени следует купить?

Поскольку линия ограничения на фонд рабочего времени движется параллельно своему исходному положению в направлении от начала координат, она стремится к точке пересечения ограничений на листовой металл и металлические стержни к точке С. Если и далее снижать жесткость ограничения на фонд рабочего времени, то оно перестанет быть лимитирующим, и дальнейшее привлечение дополнительного рабочего времени нецелесообразно. Максимальное число дополнительных человеко-часов можно определить, решив систему ограничений, линии которых пересекаются в точке С:

Листовой металл: 5 X₁ + 2 X₂ = 10000.

Металлические стержни: 2 X₁ + 5 X₂ = 10000.

Её решением являются следующие значения переменных:

X₁ = 10000/7 и X₂ = 10000/7 в неделю.

Число используемых в точке С человеко-часов равно:

X₁ + X₂ = 10000/7 + 2(10000/7) = 4285,7 чел.-ч в неделю.

Это значение на 285,7 чел.-ч превосходит первоначальное максимальное значение 4000 чел.-ч. Получение максимального сверхнормативного запаса в 285,7 чел.-ч в неделю целесообразно при условии, что стоимость единицы дополнительного человеко-часа не превосходит 17,50 усл. ед. в неделю. Если сверхнормативное количество часов рабочего времени используется максимально, то новое максимальное значение еженедельного дохода составит:

Fmax = 30× 10000/7 + 40× 10000/7

Дополнительная стоимость равна 10000 усл.ед. в неделю.

Важно уяснить, что из дохода вычитаются только те издержки, которые не фигурируют в исходной постановке задачи. Предположим, например, что при производстве автомобильных деталей стоимость одного часа рабочего времени равна 4,00 усл.ед. При расчете дохода, приходящегося на единицу деталей каждого типа, бухгалтер будет использовать именно эту стоимость. Если привлекается дополнительный фонд рабочего времени, к примеру, сверхурочная работа по 6,00 усл.ед. за 1 чел.-ч, то из них 4,00 усл.ед. уже учтены в показателях единичного дохода. Отдельно в счет нужно внести только дополнительные 2 усл.ед. за час.

Воздействие на оптимальное решение изменений в обеспечении нелимитирующими ресурсами. В примере 2 рассматривались два лимитирующих ограничения на труд илистовой металл. Остальные ограничения в первоначальном оптимальном решении не являются лимитирующими. Это ограничения на:

1) производственные мощности для выпуска деталей типа X₁;

2) производственные мощности для выпуска деталей типа X₂;

3) металлические стержни;

4) постоянные заказы.

Что происходит при изменении каждого из этих ограничений? Первые три ресурса используются в меньших или равных максимальному количествах. Любое увеличение запаса этих ресурсов не будет оказывать влияния на оптимальное решение задачи. Однако на него может влиять уменьшение запасов, соответствующих трем указанным ограничениям. Увеличение жесткости одного из нелимитирующих ограничений приведет к перемещению его линии в сторону начала координат. Сначала единственным изменением будет сокращение размеров допустимого множества. Однако когда линия ограничения переместится ниже исходной оптимальной крайней точки, данное ограничение станет лимитирующим, что приведет к появлению нового оптимального решения.

Предельные значения для этих ограничений ниже максимального уровня. Так, производственные мощности для деталей типа X₁ можно сократить с 2250 до 1500 ч, т.е. на 750 ч, прежде чем это ограничение начнет оказывать воздействие на решение задачи. Производственные мощности для деталей типа X₂ могут быть сокращены с 1750 до 1250 ч, т.е. на 500 ч. Запас металлических стержней можно уменьшить с 10000 до 9250 кг, т.е. на 750 кг в неделю. Количественные выражения этих сокращений есть ни что иное, как значения остаточных переменных. С ограничениями, для которых количество ресурсов больше либо равно минимальному, все наоборот. Любое сокращение минимального количества ресурсов приведет к увеличению размеров допустимого множества, не окажет воздействия на оптимальное решение.

Любое увеличение правой части этих ограничений сначала приведет к сокращению размеров допустимого множества, а затем повлияет и на оптимальное решение. Если постоянные заказы на детали типа X₁ возрастут на 900 и достигнут 1500 деталей в неделю, оптимальное решение начнет изменяться.

Воздействие на оптимальное решение изменений в коэффициентах целевой функции. Условия, для которых составлялась задача линейного программирования, неизбежно изменяются. Чаще всего эти изменения предполагают повторное выполнение формализации задачи, но должна существовать возможность идентифицировать воздействие незначительных изменений на решение исходной задачи. Рассмотрим изменения коэффициентов целевой функции. Если цель состоит в максимизации еженедельного дохода, то изменение стоимости сырья приведет к изменению значений коэффициентов целевой функции.

Известно, что доход от выпуска единицы деталей типа X₁ может меняться. Каков промежуток значений единичного дохода, для которых а остается оптимальной крайней точкой? Единичный доход от выпуска деталей типа X₂ остается неизменным.

Перепишем уравнение дохода за неделю в следующем виде:

F = a X₁ + 40 X₂,

где а - единичный доход от выпуска деталей типа X₁.

Преобразовав это уравнение, получим

X₂ = F /40 - (a /40) X₁.

Тангенс угла наклона линии дохода за неделю равен (- а /40). В исходном положении при а = 30 усл.ед. за единицу тангенс угла наклона равен (-30/40) = - (3/4).

Если а меньше 30 усл.ед. за единицу, то наклон линии еженедельного дохода становится более пологим. В точке А линия уровня будет отклоняться в сторону лимитирующего ограничения на фонд рабочего времени. Это ведет к уменьшению оптимального значения функции F, дохода за неделю. Обратите внимание на рис. 5. Если сильно уменьшать значение параметра а, то линия уровня еженедельного дохода совпадет с ограничением на фонд рабочего времени.

Следовательно, граничным является положение линии уровня дохода, при котором она совпадает с линией лимитирующего ограничения на фонд рабочего времени. Этому положению соответствует наименьшее значение а, для которого А является оптимальной крайней точкой.

Угол наклона линии ограничения на фонд рабочего времени можно найти, преобразовав данное ограничение к виду:

X₂ = 4000/2 - 1 X₁ /2.

Тангенс угла наклона лимитирующего ограничения равен (-1/2).

Нижний предел значений находится из условия (- а /40) = - (1/2), таким образом, а = 20 усл.ед. за единицу. Следовательно, единичный доход от выпуска деталей типа X₁ может уменьшаться до 20 усл.ед. до того, как оптимум переместится из точки А в точку D.

Причем, оптимальный доход будет сокращаться, но оптимальный ассортиментный набор не изменится до тех пор, пока значение параметра а не опустится ниже 20 усл.ед. Аналогичным образом можно найти верхний предел значений а. С увеличением значения а линия еженедельного дохода становится все менее пологой и в конечном итоге окажется параллельной линии другого лимитирующего ограничения, а именно на листовой металл. Любое дальнейшее увеличение значения а вызовет изменение оптимальной крайней точки и перемещение ее в точку Е.

Граничное положение линии уровня еженедельного дохода достигается в момент ее совпадения с ограничением на листовой металл. Этому положению соответствует верхний предел значений параметра а, для которых точка А является оптимальной крайней точкой допустимого множества. Угол наклона ограничения на листовой металл можно найти, преобразовав это уравнение к виду:

X₂ = 10000/2 - (5/2) X₁.

Тангенс угла наклона лимитирующего ограничения равен (-5/2), а верхний предел параметра а находится из условия

(а /40) = -(5/2),

следовательно, а = 100 усл.ед. за единицу. Таким образом, до того как оптимальный ассортиментный набор переместится из точки А в точку Е, единичный доход от выпуска деталей типа X1 может возрасти до 100 усл.ед.

Два соответствующих предела значения единичного дохода от выпуска деталей типа X₂ можно найти аналогичным образом, если в изложенной схеме расчетов заменить X₁ на X₂. Предположим, что значение коэффициента целевой функции при X₁ является неизменным, тогда:

F = 30 X₁ + b X₂ и X₁ = F /30 - (b /30) X₂.

По мере увеличения или уменьшения параметра b граничные положения линии уровня еженедельного дохода определяются теми же двумя ограничениями, что и в предыдущем случае. Теперь необходимо записать уравнения этих ограничений так, чтобы X₁ выступал в качестве зависимой переменной:

Фонд рабочего времени: X₁ = 4000 - 2 X₂.

Тангенс угла наклона равен (- 2), следовательно, предельное значение достигается при условии (- b /30) = -2, т.е. b = 60 усл.ед. за единицу.

Листовой металл: X₁ = 10000/5 - (2/5) X₂.

Тангенс угла наклона равен (-2/5), для предельного значения выполняется условие: - (b /30) = - (2/5), следовательно, b = 12 усл.ед. за единицу.

Крайняя точка А соответствует оптимальному ассортиментному набору только до тех пор, пока доход от выпуска деталей типа X₂ изменяется в пределах от 12 до 60 усл.ед. за единицу. В случае, если показатели единичных доходов от выпуска деталей типа X₁ или X₂ будут изменяться по сравнению с их исходными значениями, значение оптимального дохода также будет отличным от 95000 усл.ед.

Контрольные вопросы

1. Что такое связывающие, несвязывающие, избыточные ограничения; дефицитные и недефицитные ресурсы?

2. Каковы предпосылки и основные задачи анализа оптимального решения на чувствительность?

3. Как графически проводится анализ изменения запаса дефицитных ресурсов?

4. Каким образом, опираясь на результаты графического анализа, можно численно рассчитать новый (улучшенный) запас дефицитного ресурса?

5. Как графически проводится анализ изменения запаса недефицитных ресурсов?

6. Каким образом, опираясь на результаты графического анализа, можно численно рассчитать новый запас недефицитного ресурса?

7. Что такое ценность дополнительной единицы i -го ресурса?

8. Как проводится графический анализ изменения коэффициентов целевой функции?

9. Как численно определить диапазон изменения коэффициентов целевой функции, не изменяющий оптимального решения?

Литература

1. Ильенкова С.Д. Производственный менеджмент [Текст]/ С.Д. Ильенкова – М.: ЮНИТИ-ДАНА, 2000.

2. Орлов И.А. Менеджмент [Текст]/ И.А. Орлов – М.: Изумруд, 2003.

3. Зайцев М.Г. Методы оптимизации управления и принятия решений: примеры, задачи, кейсы [Текст]/ М.Г. Зайцев - М.: Дело, 2008.